洛谷 P1361 小M的作物 解题报告

P1361 小M的作物

题目描述

小M在MC里开辟了两块巨大的耕地\(A\)和\(B\)（你可以认为容量是无穷），现在，小\(P\)有\(n\)中作物的种子，每种作物的种子有1个（就是可以种一棵作物）（用1...\(n\)编号）。

现在，第\(i\)种作物种植在\(A\)中种植可以获得\(a_i\)的收益，在\(B\)中种植可以获得\(b_i\)的收益，而且，现在还有这么一种神奇的现象，就是某些作物共同种在一块耕地中可以获得额外的收益，小\(M\)找到了规则中共有\(m\)种作物组合，第\(i\)个组合中的作物共同种在\(A\)中可以获得\(c1_i\)的额外收益，共同总在B中可以获得\(c2_i\)的额外收益。

小M很快的算出了种植的最大收益，但是他想要考考你，你能回答他这个问题么？

输入输出格式

输入格式：

第一行包括一个整数\(n\)

第二行包括\(n\)个整数，表示\(a_i\)第三行包括\(n\)个整数，表示\(b_i\)第四行包括一个整数\(m\)接下来\(m\)行，

对于接下来的第\(i\)行：第一个整数\(k_i\)，表示第\(i\)个作物组合中共有\(k_i\)种作物，

接下来两个整数\(c1_i\)，\(c2_i\)，接下来\(k_i\)个整数，表示该组合中的作物编号。

输出格式：

只有一行，包括一个整数，表示最大收益

数据范围

1<=k< n<= 1000,0 < m < = 1000 保证所有数据及结果不超过\(2*10^9\)。

---

这个题加深了我对最小割模型的理解。

我第一点弄明白的一点，也是最重要的一点。

最小割在数值上与最大流相等，但在本身性质上与网络流无任何关系。

它的不那么准确的定义是：在一个图中，割去权值和最小的边集，使这个图分成两个部分，切下来的那一刀叫做最小割。最小割并不唯一，但它在数值上是等于最大流的。

对于这个题的模型来说，它有一个名字叫做二者取一式问题，在具体题目中的体现即为把点集一分为二。

类似的题目有善意的投票

虽然说了最小割与网络流无关系，但只是在定义或者说是意义上，真正要到建模时，还需要将两者综合考虑。

先考虑没有额外收益情况下的建图。

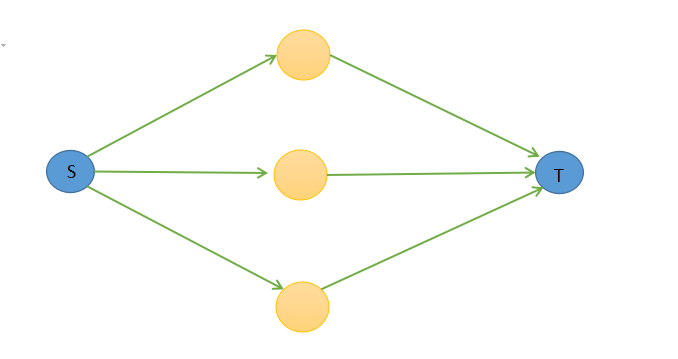
设源点S属于集合A,汇点T属于集合B，则显然点与源点所连的有向边为这个点归属于集合A所产生的收益，与汇点相连则同理。则原图边权之和-最小割就是本题的答案了。

在这个图的基础上，考虑如何把点集给加入。

首先明确一点，点集的贡献有三种情况，对集合A贡献，对集合B贡献或者不贡献。这意味着只划分出一种状态是无法描述的，至少要把A与B的情况分开描述。

讨论一个对\(A\)有贡献的点集\(\{c,d\}\)。

依据题目，我们对这个点集的要求是，只要\(c,d\)有一个点被割到了集合\(T\)，这个点集都无法产生贡献。换而言之，只要\(c\)或\(d\)在集合\(B\)，代表点集贡献的边必须要断开。

先尝试着连接这条贡献边，因为这条边不可能直接连到图中代表作物的点上，所以连接一个虚点上去。

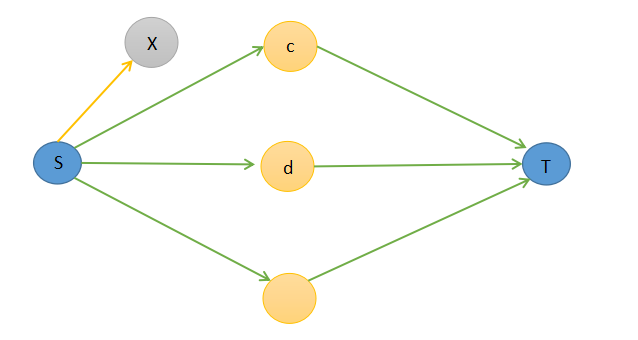
X为点集所产生的虚点。

如果\(c\)被割到了集合\(B\)，则所有从\(S\)到\(c\)的路径都得被断开（具体只路径的一条边断掉），如果我们想要黄边断掉，那么虚点\(X\)连\(c\)的那条路径不能被断掉。而容量为正无穷的边不可能被断掉，于是我们这样建图。

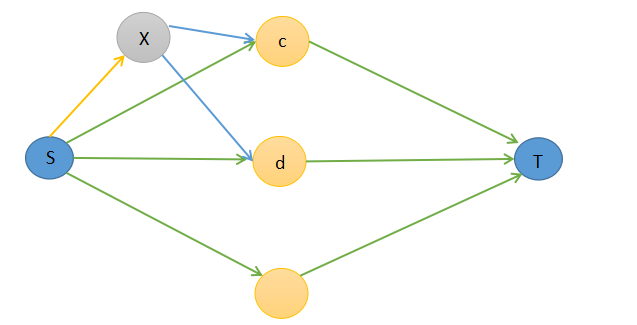
两条蓝色的边的边权为\(inf\)

对待贡献\(B\)集合的点，同理

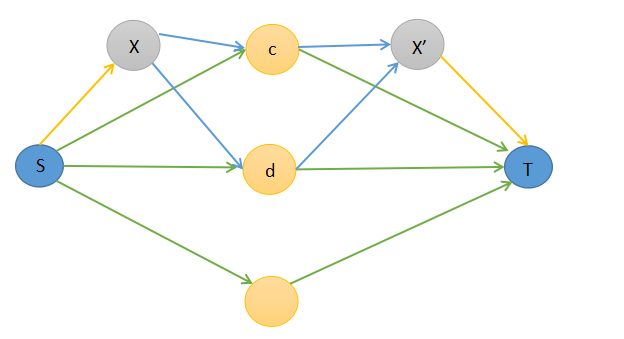
建图跑网络流即可。

要注意的一点是，这题卡常，吸氧才水过去的

---

Code

#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int N=3010;
const int M=2000100;
const int inf=0x3f3f3f3f;
int head[N],edge[M],to[M],next[M],cnt=1;
void add(int u,int v,int w)
{
    to[++cnt]=v;next[cnt]=head[u];edge[cnt]=w;head[u]=cnt;
    to[++cnt]=u;next[cnt]=head[v];edge[cnt]=0;head[v]=cnt;
}
int dep[N],used[N],pre[N],tot,s[N],ans,m,n,sum;
queue <int > q;
bool bfs()
{
    while(!q.empty()) q.pop();
    q.push(0);
    memset(dep,0,sizeof(dep));
    dep[0]=1;
    while(!q.empty()&&q.front()!=n+1)
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=next[i])
        {
            int v=to[i],w=edge[i];
            if(!dep[v]&&w)
            {
                dep[v]=dep[u]+1;
                q.push(v);
            }
        }
    }
    return !q.empty();
}
int main()
{
    scanf("%d",&n);
    int w,v,k,c1,c2;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&w);
        sum+=w;
        add(0,i,w);
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&w);
        sum+=w;
        add(i,n+1,w);
    }
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&k,&c1,&c2);
        add(0,i+n+1,c1);sum+=c1;
        add(i+n+m+1,n+1,c2);sum+=c2;
        for(int j=1;j<=k;j++)
        {
            scanf("%d",&v);
            add(i+n+1,v,inf);
            add(v,i+n+m+1,inf);
        }
    }
    while(bfs())
    {
        memset(used,0,sizeof(used));
        s[++tot]=0;
        while(tot)
        {
            int u=s[tot];
            if(u==n+1)
            {
                int mi=inf,id;
                for(int i=tot;i>1;i--)
                    if(mi>=edge[pre[s[i]]])
                    {
                        mi=edge[pre[s[i]]];
                        id=i;
                    }
                ans+=mi;
                for(int i=tot;i>1;i--)
                {
                    edge[pre[s[i]]]-=mi;
                    edge[pre[s[i]]^1]+=mi;
                }
                tot=id-1;
                used[n+1]=0;
            }
            else
            {
                for(int i=head[u];i;i=next[i])
                {
                    int v=to[i],w=edge[i];
                    if(!used[v]&&dep[v]==dep[u]+1&&w)
                    {
                        used[v]=1;
                        s[++tot]=v;
                        pre[v]=i;
                        break;
                    }
                }
                if(u==s[tot]) tot--;
            }
        }
    }
    printf("%d\n",sum-ans);
    return 0;
}

---

2018.6.28