混沌分形之马丁(Martin)迭代

我不记得从什么地方看到的这种分形图形生成方式，再到网上找竟然一时没查到任何相关资料。没关系，总之这种图形也很漂亮多变，并且其算法比较简单。只是我最后生成的图像有点瘆人,密集恐惧症患者慎入。

相关代码如下：

class MartinIterate : public FractalEquation
{
public:
    MartinIterate()
    {
        m_StartX = 1.0f;
        m_StartY = 1.0f;
        m_StartZ = 0.0f;

        m_ParamA = 0.68f;
        m_ParamB = 0.75f;
        m_ParamC = 0.83f;
    }

    void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
    {
        if (x > FLT_EPSILON)
        {
            outX = y - sqrtf(fabsf(m_ParamB*x - m_ParamC));
        }
        else if (x < -FLT_EPSILON)
        {
            outX = y + sqrtf(fabsf(m_ParamB*x - m_ParamC));
        }
        else
        {
            outX = y;
        }

        outY = m_ParamA - x;

        outZ = z;
    }

    bool IsValidParamA() const {return true;}
    bool IsValidParamB() const {return true;}
    bool IsValidParamC() const {return true;}

    bool Is3D() const {return false;}
};

关于基类FractalEquation的定义及相关软件见：混沌与分形

点集图形：

以此算法生成的图像如下：

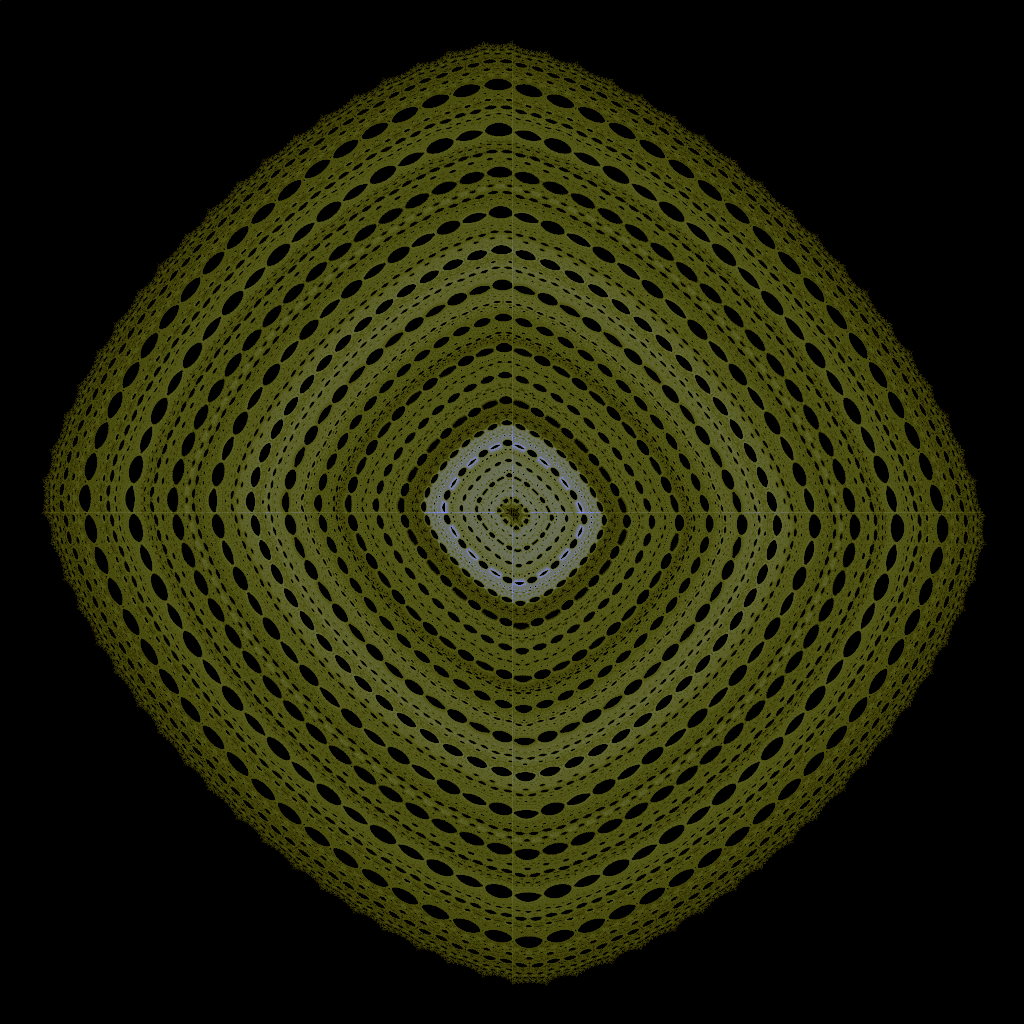
我想这几幅图有密集恐惧症的人一定看不下去，而我看到它时总会想到一种东西叫“莲蓬乳”。