Verilog 加法器和减法器(2)

类似半加器和全加器，也有半减器和全减器。

半减器只考虑当前两位二进制数相减，输出为差以及是否向高位借位，而全减器还要考虑当前位的低位是否曾有借位。它们的真值表如下：

对半减器，diff = x ^y, cin = ~x&y

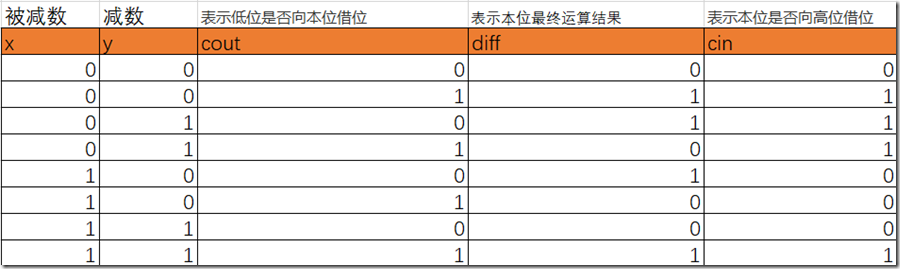
对全减器，要理解真值表，可以用举列子的方法得到，比如4’b1000-4b'0001,则第一位对应0 1 0 1 1第二位对应的是0 0 1 1 1

从真值表中，可以得到 diff = x ^ y ^cout, cin = (~x&(y^cout))|(y&cout)

推导过程：diff = ~x&~y&cout + ~x&y&~cout +x&~y&~cout+x&y&cout=~x&(~y&cout+y&~cout)+x&(~y&~cout+y&cout)=~x&(y^cout)+x&~(y^cout)=x^y^cout;

cin = ~x&~y&cout+~x&y&~cout+~x&y&cout+x&y&cout=~x&(~y&cout+~x&~cout)+(~x+x)&y&cout=~x&(y^cout)+y&cout

注意：这儿 +和|都表示或。

半减器的verilog代码和testbench代码如下：

module halfsub(x,y,d,cin);

  input x;
  input y;

  output d;
  output cin;

  assign d = x^y;
  assign cin = (~x)&y;

endmodule

`timescale 1ns/1ns
`define clock_period 20

module halfsub_tb;
  reg  x,y;

  wire cin; //carryover
  wire d;
  reg clk;

  halfsub halfsub_0(
						.x(x),
						.y(y),
						.d(d),
						.cin(cin)
                  );

  initial clk = 0;
  always #(`clock_period/2) clk = ~clk;

  initial begin
     x = 0;
     repeat(20)
	    #(`clock_period) x = $random;

  end

  initial begin
     y = 0;
     repeat(20)
	    #(`clock_period) y = $random;

  end

  initial begin
     #(`clock_period*20)
	  $stop;
  end

endmodule

用rtl viewer，可以看到半减器逻辑图如下：

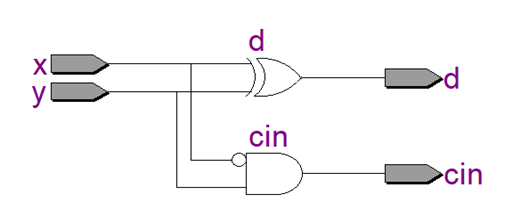
半减器功能验证的波形：

全减器的verilog代码和testbench代码如下：

module fullsub(cout,x,y,d,cin);

  input cout; // carry out bit, borrowed by its next low bit
  input x;
  input y;

  output d;
  output cin;

  assign d = x^y^cout;
  assign cin = (~x&(y^cout))|(y&cout);

endmodule

`timescale 1ns/1ns
`define clock_period 20

module fullsub_tb;
  reg  x,y,cout;

  wire cin; //carryover
  wire d;
  reg clk;

  fullsub fullsub_0(
                  .cout(cout),
						.x(x),
						.y(y),
						.d(d),
						.cin(cin)
                  );

  initial clk = 0;
  always #(`clock_period/2) clk = ~clk;

  initial begin
     x = 0;
     repeat(20)
	    #(`clock_period) x = $random;

  end

  initial begin
     y = 0;
     repeat(20)
	    #(`clock_period) y = $random;

  end

   initial begin
     cout = 0;
     repeat(20)
	    #(`clock_period) cout = $random;

  end

  initial begin
     #(`clock_period*20)
	  $stop;
  end

endmodule

用rtl viewer，可以看到全减器逻辑图如下：

全减器的功能验证波形：