Albert理论详解：用矩阵分解与跨层参数共享减少参数量

1.介绍

Albert是Bert的一个变种，它在Bert的基础上减少了参数量，使整个模型更加的“轻量化”，同时也保持了Bert的性能，但值得注意的是，Albert虽然显著地减少了参数量，但并没有显著地减少计算时间复杂度，换言之，Albert的预测速度不一定比普通的更快，甚至可能会减慢训练的速度。（Albert只降参数量，而不减少计算量）

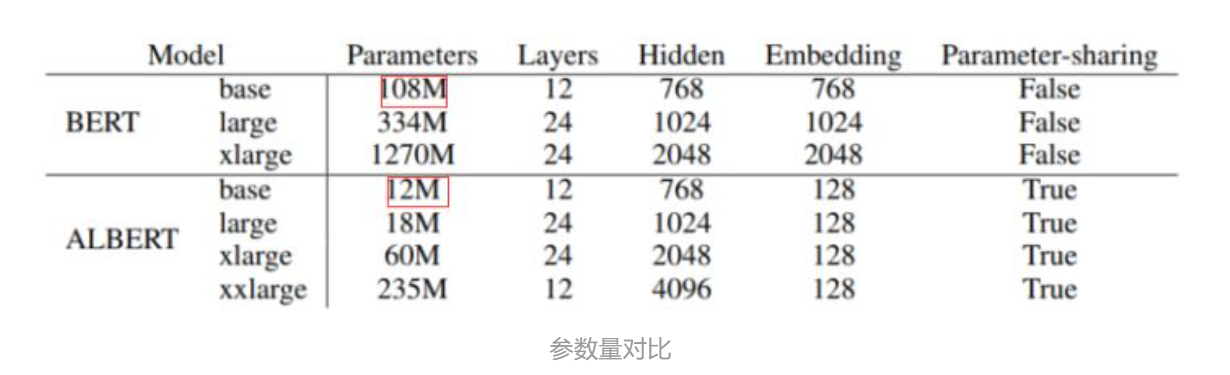
如上图所示，在base、large、xlarge这三个不同体量的模型上，Albert的参数量对比Bert均有十分明显的减少。

Albert之所以能够实现如此有效的参数缩减，原因在于它的两个特殊的机制：Factorized embedding parameterization（矩阵分解） 与 Cross-layer parameter sharing（跨层参数共享），下面将对这两个机制进行详细的介绍。

2.Factorized embedding parameterization（矩阵分解）

这一机制主要作用与embedding层上，在Bert（包括所有基于Bert的变体模型）中，为了从此表中提取特征并降维，我们首先要使用一个embedding层对输入数据进行处理。embedding的大小为词汇表的长度V乘以每个字/单词的embedding隐藏层大小H。 也就是说，一个embedding层的参数量为\(V×H\)，而在Albert中，作者通过一个参数\(E\)来分解这个embedding矩阵，从而使得整体的embedding参数变小，于是\(V×H\)就转变为了\(V×E+E×H\)，如果将embedding矩阵按照这种方式分解，最后得到的结果维度是不变的，依旧是\(L×H\)（\(L\)是句子长度），但如果此时，当\(E\)远小于\(H\)时，那么模型所需的参数量就会大大减少。实验证明，当\(E=128\)时效果最好。

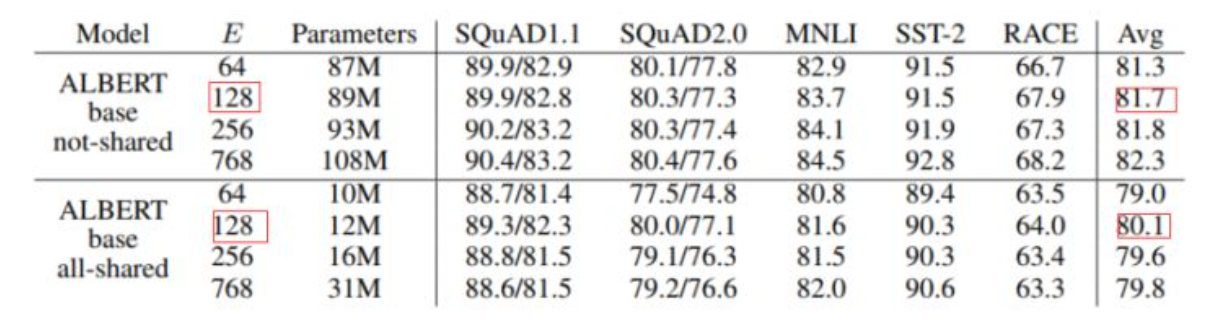
在Bert中，embedding层的\(H\)一般设定为\(768\)，此时如果\(V\)的值为\(21000\)，且\(E\)的值为\(128\)，那么在使用矩阵分解前，参数量为\(21000×768=16128000=16M\)，在使用矩阵分解后，参数的量为\(21000×128+128×768=2786304=2.7M\)，由此可见，矩阵分解能够在一定程度上降低参数的量，但Albert最核心的机制并非矩阵分解，而是下面要介绍的Cross-layer parameter sharing（跨层参数共享）

3.Cross-layer parameter sharing（跨层数参数共享）

这是Albert的核心机制。

在Bert中，我们共有12个self-attention层，每一层的结构如下所示：

有趣的地方来了，Albert的作者经过研究发现，虽然Bert中有着12个self-attention层，但是，如果把每一层的参数都提取出来，会发现每一层的参数都基本相似。因此Albert的作者索性将一个self-attention层复制12次，用这12个完全相同的self-attention层取代原先12个不同的self-attention层。在训练时，我们其实只对一层self-attention进行训练，但在计算时，由于我们将这一层计算了12次，所以计算速度并没有显著地降低。

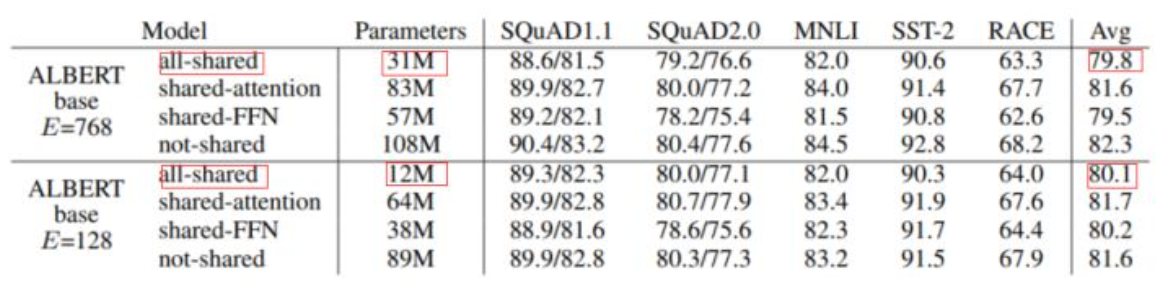
上图是几种不同的共享形式，all-shared降低的参数量最大，但同时会对最后的效果产生一定的影响，如果担心影响实际效果，可以选择shared-attention。Albert默认使用的是all-shared。

4.Albert与Bert的效果对比

作者在论文中将Bert与Albert进行了对比，对比的内容包括参数量、计算时间以及数据集评价指标：

在上图中，计算速度体现在Speedup列，并以BERT-large的基准。例如，Bert-base的计算速度为4.7x，就代表Bert-base的计算速度时Bert-large的4.7倍（以此类推），但上表也表现出一个较为重要的问题：Albert的计算速度对比Bert其实并没有多大的提升，但同时，由于减少了参数的量，还会对模型的性能产生一定的影响。

考虑到这一点，作者还拿Bert-large与Albert-xxlarge进行了对比，结果如下表所示:

在上表中，Albert以较小的step，差不多的训练时间，在不同的数据集上取得了比Bert更好的效果。但考虑到实际使用时，参数量减少给训练结果带来的负面影响，Albert是否比Bert优秀还是要另当别论。

最后附上一个Albert中文预训练模型的huggingface链接：

https://huggingface.co/voidful/albert_chinese_base