有限差分法（Finite Difference Method）解方程：边界和内部结点的控制方程

FDM解常微分方程

问题描述

\[\frac{d^2\phi}{dx^2}=S_{\phi} \tag{1}
\]

这是二阶常微分方程（second-order Ordinary Differential Equation, ODE），考虑最简单的情况即\(S=0\)，积分后可得\(\phi=c_1x+c_2\)，有两个待定系数，因此要求解该方程必须提供两个边界条件（因为方程中不包含时间项，因此无初始条件），例如

\[\phi(x_L)=\phi_L \quad \phi(x_R)=\phi_R
\]

场和边界

我们把上述方程转化为一个场（field）。试想存在一维（因为\(\phi\)仅与一个变量有关）直线，线上有若干等距分布的结点（node），每个结点都有唯一的\(\phi\)，那么\(\phi\)和\(x\)的关系满足上述方程。

内部结点满足方程，那么边界上的\(\phi(x_L)\)和\(\phi(x_R)\)呢？事实上，边界应是内部结点的延申，即边界点也应该满足上述方程。这也是为什么我们可以通过两个边界条件求解\(\phi=c_1x+c_2\)的原因，这隐含的假设就是边界点满足常微分方程。

结点上的值

用数值方法求解上述方程等价于求解场内每个结点上的\(\phi\)，结点\(i\)的上式表达为

\[\frac{d^2\phi}{dx^2}\bigg|_{i}
\]

如何从结点值\(\phi_i\)得到导数值？很自然想到用Taylor展开。需要注意的是，Taylor展开隐含的假设是\(\phi\)无限可导。将\(i\)关于周围两点做Taylor展开，即

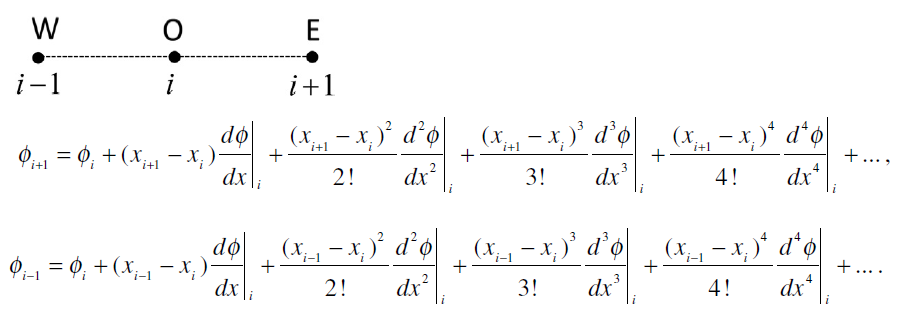
假设等距，则

\[\frac{d^2\phi}{dx^2}\bigg|_{i} =\frac{\phi_{i+1}+\phi_{i-1}-2\phi_i}{(\Delta x)^2}-\frac{(\Delta x)^2}{12} \frac{d^4\phi}{dx^4}\bigg|_{i} + ... \tag{2}
\]

\[\varepsilon_i=-\frac{(\Delta x)^2}{12} \frac{d^4\phi}{dx^4}\bigg|_{i} + ...
\]

其中\(\varepsilon_i\)为离散误差或截断误差（discretization or truncation error），该误差正比于距离的平方，因此我们称上式对导数的逼近有二阶精度。

边界条件

上一部分是对场内部结点的推导。边界上结点的值为边界条件，有以下三种形式：

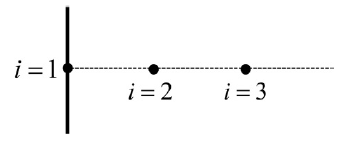
Dirichlet

\[\phi_{i=1}=\phi_L
\]

Neumann

\[\frac{d\phi}{dx}\bigg|_{i=1}=J_L \tag{3}
\]

将结点2关于结点1做Taylor展开，可以得到一阶精度的梯度表达式

\[\frac{d\phi}{dx}\bigg|_{i=1}=\frac{\phi_2-\phi_1}{\Delta x}+\varepsilon(\Delta x) \tag{4}
\]

将结点3关于结点1做Taylor展开，结合上式可以进一步得到二阶精度

\[\frac{d\phi}{dx}\bigg|_{i=1}=\frac{4\phi_2-\phi_3-3\phi_1}{2\Delta x}+\varepsilon(\Delta x^2) \tag{5}
\]

对于非Dirichlet的边界条件，应尽量让边界条件也满足内部结点的控制方程。

对\(\phi_2\)和\(\phi_3\)关于结点1展开可得

\[\phi_2=\phi_1+(\Delta x)\frac{d\phi}{dx}\bigg|_{i=1}+... \\
\phi_3=\phi_1+(2\Delta x)\frac{d\phi}{dx}\bigg|_{i=1}+...
\]

将边界条件公式(3)代入上式可得

\[\phi_2=\phi_1+(\Delta x)J_L+... \\
\phi_3=\phi_1+(2\Delta x)J_L+...
\]

将上式整理可得结点1满足的二阶导数项：

\[\frac{d^2\phi}{dx^2}\bigg|_{i=1}=\frac{8\phi_2-\phi_3-7\phi_1-(6\Delta x)J_L}{2(\Delta x)^2}+\varepsilon(\Delta x^2) \tag{6}
\]

上式为结点1满足的控制方程，并用上了梯度边界条件。需要说明的是，不用公式(6)而用公式(4,5)同样可以求解问题，但是前者的精度更高。

Robin

\[\alpha \phi_1 + \beta \frac{d\phi}{dx}\bigg|_{i=1}=\gamma
\]

类似地，令边界结点1既满足控制方程又满足边界条件。对上式移项可得

\[\frac{d\phi}{dx}\bigg|_{i=1}=\frac{\gamma-\alpha \phi_1}{\beta}
\]

同样代入\(\phi_2\)和\(\phi_3\)的Taylor展开，

\[\phi_2=\phi_1+(\Delta x) \left( \frac{\gamma-\alpha \phi_1}{\beta} \right) +... \\
\phi_3=\phi_1+(2\Delta x) \left( \frac{\gamma-\alpha \phi_1}{\beta} \right) +...
\]

消去三阶导数项并移项可得

\[\frac{d^2\phi}{dx^2}\bigg|_{i=1}=\frac{8\phi_2-\phi_3-7\phi_1-(6\Delta x)J_L}{2(\Delta x)^2}+\varepsilon(\Delta x^2) \tag{7}
\]

其中

\[J_L=\frac{d\phi}{dx}\bigg|_{i=1}=\frac{\gamma-\alpha \phi_1}{\beta}
\]

组建矩阵

有了内部结点的离散格式和边界条件，我们便可对每个结点列方程。由于结点\(i\)离散格式中势必会包含其他结点信息，例如对结点\(i\)

\[A_{i,1}\phi_1 + ... + A_{i,i-1}\phi_{i-1} + A_{i,i}\phi_i + A_{i,i+1}\phi_{i+1} + ... + A_{i,N}\phi_N =Q_i
\]

将所有结点的方程组合起来，借助矩阵运算求解。

FDM求解泊松方程：二维问题

二维Poisson方程：

\[\nabla^2 \phi=\frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} = S_{\phi} \tag{8}
\]

如果\(S_{\phi}=0\)，则退化为Laplace方程。二阶偏导数项同样使用Taylor展开，只不过针对该问题应使用二维展开。如果使用正交网格结点，则相当于在每一维独自做Taylor展开。

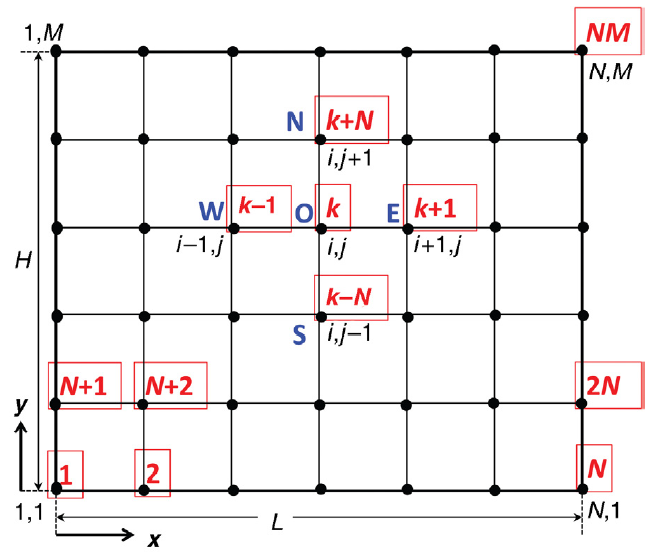
按上图所示，网格结点可分为内部结点和边界结点。

内部结点控制方程

由上文公式(2)可知，两个二阶偏导数项可分别写为

\[\frac{\partial^2\phi}{\partial x^2}\bigg|_{i,j} =\frac{\phi_{i+1,j}+\phi_{i-1,j}-2\phi_{i,j}}{(\Delta x)^2} + \varepsilon(\Delta x^2) \tag{9}
\]

\[\frac{\partial^2\phi}{\partial y^2}\bigg|_{i,j} =\frac{\phi_{i,j+1}+\phi_{i,j-1}-2\phi_{i,j}}{(\Delta y)^2} + \varepsilon(\Delta y^2) \tag{10}
\]

去掉高阶项，可得内部结点控制方程

\[\frac{\phi_{i+1,j}+\phi_{i-1,j}-2\phi_{i,j}}{(\Delta x)^2} + \frac{\phi_{i,j+1}+\phi_{i,j-1}-2\phi_{i,j}}{(\Delta y)^2} \approx S_{i,j} \tag{11}
\]

下边界

Robin边界条件

\[\alpha \phi (x,0) + \beta \frac{\partial \phi}{\partial y}\bigg|_{x,0} = \gamma
\]

对于下边界的某个非边角结点\((i,1)\)，其中\(i\neq 1, i\neq N\)，根据公式(7)来构建既满足边界条件又满足内部结点控制方程的离散格式，即公式(7)

\[\frac{\partial^2\phi}{\partial y^2}\bigg|_{i,1} = \frac{8\phi_{i,2}-\phi_{i,3}-(7-6\Delta y \frac{\alpha}{\beta}) \phi_{i,1} - 6\Delta y (\gamma / \beta)}{2(\Delta y)^2} \tag{12}
\]

而下边界上\(x\)的二阶偏导数项仍按照公式(9)离散。因此，下边界结点的控制方程由公式(9)和(12)组成。

右边界

Neumann边界条件

\[\frac{\partial\phi}{\partial x}\bigg|_{L,y} = J_R
\]

使用公式(6)得到\(x\)的二阶偏导数项，即

\[\frac{\partial^2\phi}{\partial x^2}\bigg|_{N,j}=\frac{8\phi_{N-1,j}-\phi_{N-2,j}-7\phi_{N,j}-(6\Delta x)J_R}{2(\Delta x)^2} \tag{13}
\]

而\(y\)的二阶偏导数项仍用公式(10)。右下角的结点\((N,1)\)应同时满足Robin和Neumann边界条件，该结点的\(x\)偏导数项应使用公式(13)，\(y\)应使用公式(12)

上边界和左边界

Dirichlet边界条件：

\[\phi(0,y)=\phi_L \\
\phi(x,H)=\phi_T
\]