吴恩达老师机器学习课程chapter02——分类

吴恩达老师机器学习课程chapter02——分类

本文是非计算机专业新手的自学笔记，高手勿喷，欢迎指正与其他任何合理交流。

本文仅作速查备忘之用，对应吴恩达(AndrewNg)老师的机器学期课程第六章。

---

目录

• 吴恩达老师机器学习课程chapter02——分类
  • 二分类
    • 基本概念
    • 代价函数
  • 多分类

---

二分类

流入垃圾邮件的分类，或去医院医生诊断病人身体里的肿瘤是否是恶性的，这些是常见的分类问题。

抽象成数学关系后，输出y为整数，这样的问题被称之为分类问题。

基本概念

例题如下：

可以看出，当出现偏离所有样本均值很远的样本时，很有可能导致简单的线性回归结果判断不准。且hθ(x)可以大于0或者小于1。

因此，有需要引入Sigmoid函数，又名Logistic函数。这种函数平滑、易于求导。可以将一个实数映射到(0,1)的区间，可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。这里将Sigmoid函数记为：

\[g(z)=\frac{1}{1+e^{-z} }
\]

与线性回归结合可得：

\[h_{\theta }(x) =g(\theta ^{T}x )=\frac{1}{1+e^{-\theta ^{T}x } }
\]

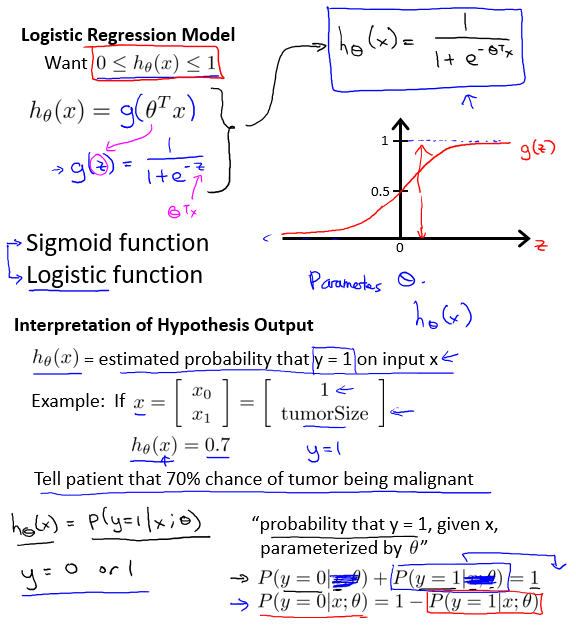
这里hθ(x)可以用来表征 概率 。

hθ(x) ≥ 0.5，认为y=1；否则，认为y=0。

运用 非线性的多项式回归 ，可以实现 ** 非线性分类 **：

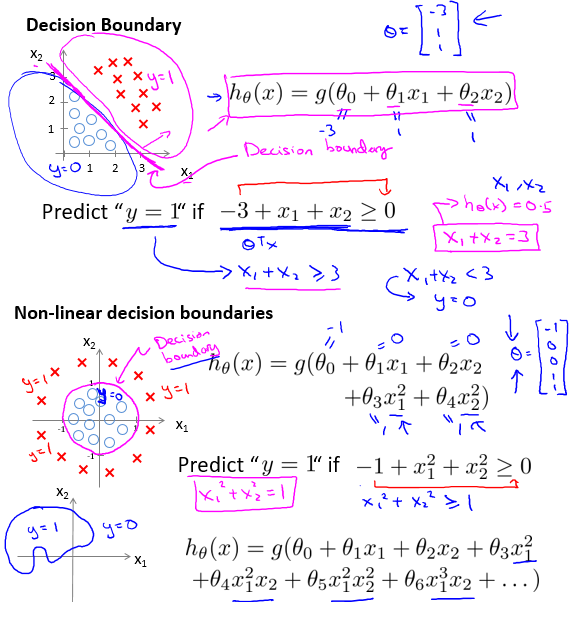
代价函数

若选择线性回归中的代价函数，那么的得到的函数很可能不是凸函数(convex function)，梯度下降法只能得到局部最优，在此失效。

这里定义对数回归代价函数(logistic regression cost function)：

\[\operatorname{Cost}\left({h_{\theta}(x)}, y\right)=\left\{\begin{array}{ll}
-\log \left(h_{\theta}(x)\right) & \text { if } y=1 \\
-\log \left(1-h_{\theta}(x)\right) & \text { if } y=0
\end{array}\right.
\]

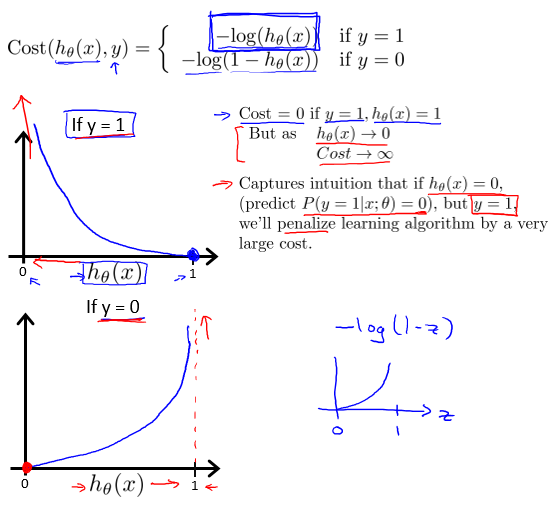
由图可见：

y=1时，若 hθ(x) → 0，惩罚很大；y=0时，若 hθ(x) → 1，惩罚很大。

将所有样本的Cost叠加取均值，可得：

\[\begin{aligned}
J(\theta) &=\frac{1}{m} \sum_{i=1}^{m} \operatorname{Cost}\left(h_{\theta}\left(x^{(i)}\right), y^{(i)}\right) \\
&=-\frac{1}{m}\left[\sum_{i=1}^{m} y^{(i)} \log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]
\end{aligned}
\]

故问题转化为可以用梯度下降法 解决的优化问题如下:

其中的梯度：

---

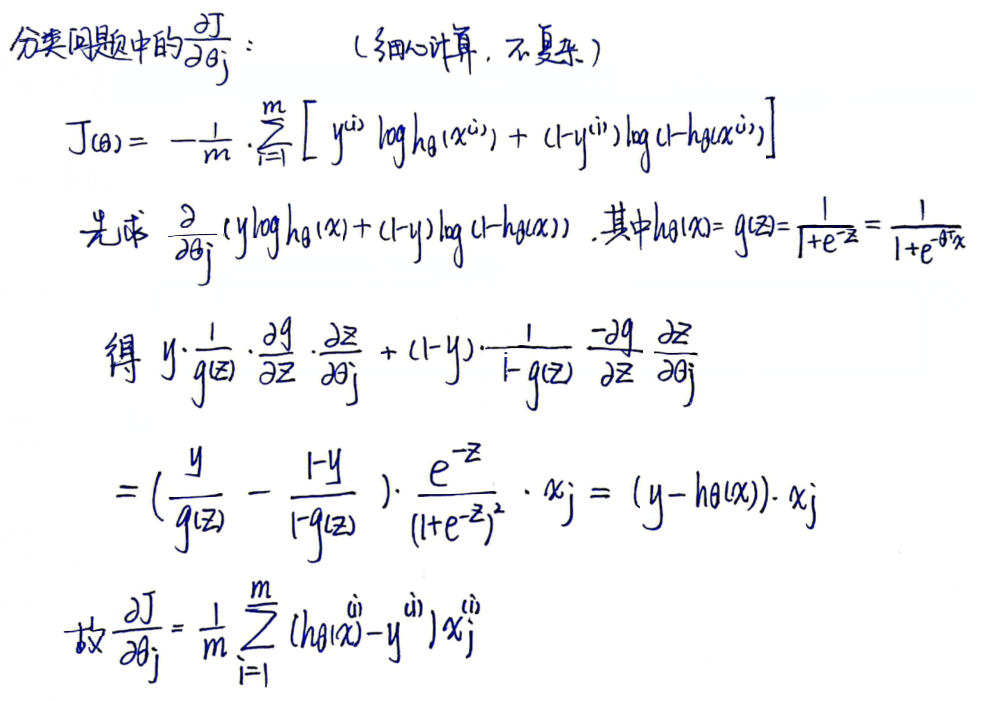
多分类

对于有n个类别的多分类，可以视为n个二分类问题：

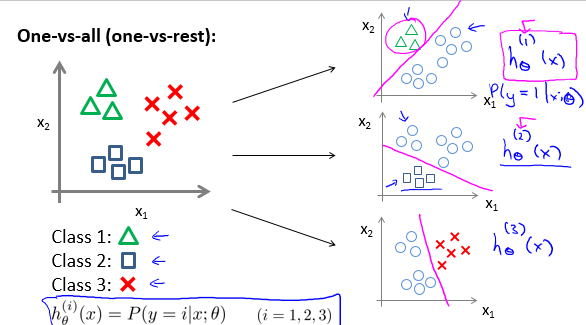
首先，训练n个训练器 $ h_{\theta}^{(i)}(x) $；

接着将新的输入x代入这n个分类器当中,选择概率最大的一个，即 $ \max {i} h^{(i)}(x)$。