算法竞赛进阶指南0x34矩阵乘法

文章目录

• 矩阵的相关性质再回顾
• 矩阵加速大法：
• • ACWing205. 斐波那契
  • • 代码
  • ACWing206. 石头游戏
  • • 解题思路：
    • 感受：
    • 代码

矩阵的相关性质再回顾

对于一个矩阵

1. 满足结合律
2. 满足乘法对于加法的分配率
3. 但是不满足交换律！

对于特殊一点的矩阵来说:

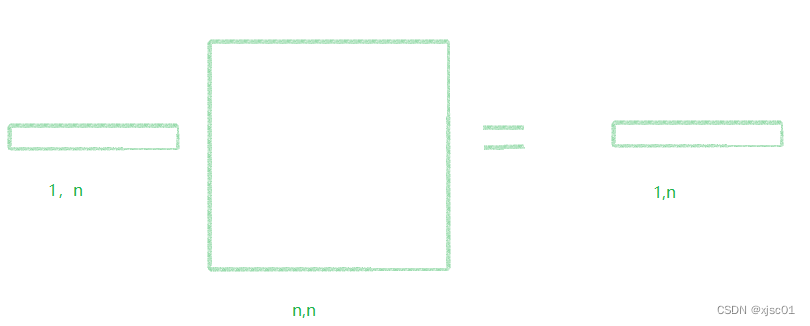
把最左边还有最右面的看成一个数组。。

矩阵加速大法：

因为矩阵满足结合律，所以可以使用快速幂来进行计算。
规律总结：
矩阵加速设计到两个东西：

• 状态矩阵
• 转移矩阵

1. 可以抽象出一个一维向量，在每一次递推就变化一次；
2. 状态转移方程不发生变化；
3. 状态转移过程中，一定是线性的（加减，乘以系数）
4. 注意：状态矩阵需要尽可能短，转移次数可以比较大。

时间复杂度是

N

3

l

o

g

N

N^3logN

N3logN.

ACWing205. 斐波那契

要注意取模

代码

#include <bits/stdc++.h>
using namespace std;
const int len = 2;
const int mod = 10000;
void mulself(int a[2][2])
{
    int c[2][2];
    memset(c, 0, sizeof(c));
    for(int i = 0; i < len; i++ )
        for(int j = 0; j < len; j++)
            for(int k = 0; k < len; k++)
                c[i][j] = (c[i][j]+(long  long)a[i][k] * a[k][j])%mod;
    memcpy(a, c, sizeof(c));
}
void mul(int a[2][2], int f[2])
{
    int c[2];
    memset(c, 0, sizeof(c));
    for(int j = 0; j < len; j++)
        for(int k = 0; k < len; k++)
            c[j] = (c[j] + (long long)f[k] * a[k][j])%mod;
    memcpy(f, c, sizeof(c));
}
void solve(int n)
{
    int a[2][2] = {{0, 1}, {1, 1}};
    int f[2] = {0, 1};
    for(; n; n >>= 1 )
    {
        if(n&1) mul(a, f);
        mulself(a);
    }
    printf("%d\n", f[0]);
}
int main()
{
    int n;
    while((scanf("%d", &n)||1) && n != -1) solve(n);
    return 0;
}

ACWing206. 石头游戏

解题思路：

感受：

太恶心了，一百多行代码，debug了一下午

代码

//在这个程序中所有的数组全部从1开始计数
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,m,t,act;
char op[20][20];//表示操作
ll oplen[20];
ll mp[70];//表示单元格映射的操作数字
ll matrix[70][70][70];
ll p;//p表示状态矩阵的从 0 到 p；
inline ll num(ll x, ll y)
{
    if(x==0 && y==0) return 0;
    return (x-1)*m + y;
}
void read_op_and_mp()
{
    char buf[12];
    for(int i = 1; i <= n; i++)
    {
        scanf("%s", buf+1);
        for(int j = 1; j <= m; j++)
        {
            mp[num(i, j)] = buf[j]-'0'+1;
        }
    }
    for(int i = 1; i <= act; i++)
    {
        scanf("%s", op[i]+1);
        oplen[i] = strlen(op[i]+1);
    }
}
void mulself(ll a[70][70])//
{
    ll c[70][70];
    memset(c, 0, sizeof(c));
    for(int i = 0; i<= p; i++)
        for(int j = 0; j <= p; j++)
            for(int k = 0; k <= p; k++)
                c[i][j] += a[i][k] * a[k][j];
    memcpy(a, c, sizeof(c));
}
void mul(ll f[], ll a[70][70])
{
    ll c[70];
    memset(c, 0, sizeof(c));
    for(int j = 0; j <= p; j++)
        for(int k = 0; k <= p; k++)
        {
            c[j] += f[k] * a[k][j];
        }
    memcpy(f, c, sizeof(c));//sizeof不能是f因为f是指针。
}
void make_matrix()
{
    ll  tmp[70][70];
    for(int i = 0; i <= p; i++) matrix[0][i][i] = 1;//设置为单位矩阵
    for(int tt = 1; tt <= 60; tt++)
    {
        memset(tmp, 0, sizeof(tmp));
        tmp[0][0] = 1;
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= m; j++)
            {
                char ch = op[mp[num(i, j)]][(tt-1)%oplen[mp[num(i, j)]]+1];
                if('0' <= ch && ch <= '9')
                {
                    tmp[num(0, 0)][num(i, j)] = ch-'0';
                    tmp[num(i, j)][num(i, j)] = 1;
                }
                else if(ch=='N')
                {
                    if(i > 1) tmp[num(i, j)][num(i-1, j)] = 1;
                }
                else if(ch=='W')
                {
                    if(j > 1) tmp[num(i, j)][num(i, j-1)] = 1;
                }
                else if(ch=='S')
                {
                    if(i < n) tmp[num(i, j)][num(i+1, j)] = 1;
                }
                else if(ch=='E')
                {
                    if(j < m) tmp[num(i, j)][num(i, j+1)] = 1;
                }
            }
        for(int i = 0; i <= p; i++)
            for(int j = 0; j <= p; j++)
                for(int k = 0; k <= p; k++)
                {
                    matrix[tt][i][j] += matrix[tt-1][i][k] * tmp[k][j];
                }
    }
}
ll solve()
{
    ll ret = 0;
    ll f[70] = {0};
    f[0] = 1;
    ll a[70][70];
    make_matrix();
    memcpy(a, matrix[60], sizeof(a));
    ll xx = t / 60;
    for(; xx; xx >>= 1)
    {
        if(xx&1) mul(f, a);
        mulself(a);
    }
    mul(f, matrix[t%60]);
    for(int i = 1; i <= p; i++) ret = max(ret, f[i]);
    return ret;
}
int main()
{
    cin >> n >> m >> t >> act;
    read_op_and_mp();
    p = m * n;
    ll ans = solve();
    cout << ans << endl;
    return 0;
}