CSU 1351 Tree Counting

　　原题链接：http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1351

　　DP题，毫无疑问。由于动态规划题目做得少、不熟悉，刚开始自己用f[i]表示用 i 个节点的方案数，然后就需要逐个子节点进行深搜，非常暴力，毫无疑问TLE。在此情况下，直觉告诉我需要增加一维空间来降低时间复杂度。此时，设dp[i][j]表示用 i 个节点，孩子节点数恰好为 j 的方案数，那么，状态转移方程为：

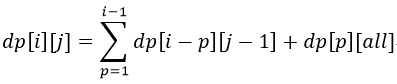
#include <stdio.h>
#include <string.h>
#include <iostream>
using namespace std;

#define N 205
#define M 25
#define MOD 1000000007 

typedef long long LL;

LL dp[N][M];

int main()
{
    int t, n, k;
    cin >> t;
    while(t--)
    {
        cin >> n >> k;
        memset(dp, , sizeof dp);
        dp[][] = ; dp[][] = ;
        for(int i = ; i <= n; i++)
        {
            dp[i][] = dp[i-][];
            for(int j = ; j <= k; j++)
            {
                if(j >= i) break;
                for(int p = ; p < i-; p++)
                {
                    dp[i][j] = (dp[i][j] + dp[i-p][j-] * dp[p][]) % MOD;
                }
            }
            for(int j = ; j <= k; j++)
                dp[i][] = (dp[i][] + dp[i][j]) % MOD;
        }
        cout << dp[n][] << endl;
    }
    return ;
}