4.1、支持向量机(SVM)
1、二分类问题
在以前的博客中,我们介绍了用于处理二分类问题的Logistic Regression算法和用于处理多分类问题的Softmax Regression算法,典型的二分类问题,如图:
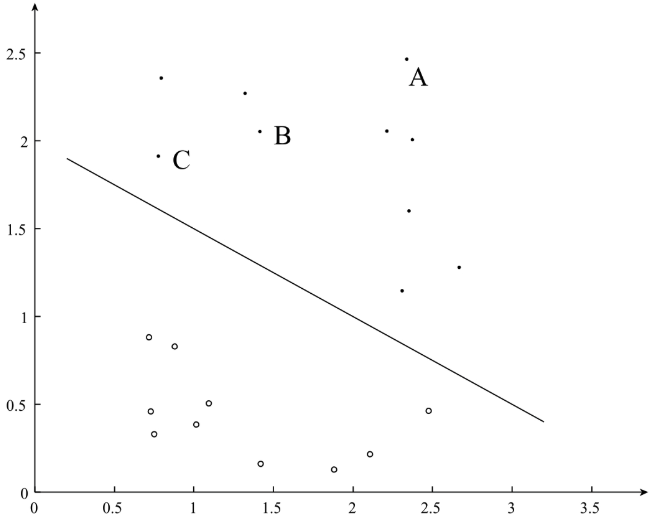
对于上图的二分类问题中,“.”表示的是正类,“。”表示的是负类。我们试图寻找到图中的分隔平面,能够分隔图中的正负样本,其中,分隔超平面为:

最终的到的分类决策函数:
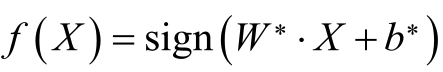
其中,函数sign(x)为符号函数:
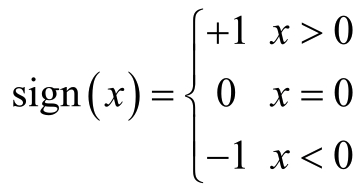
其中,当W*X+b*>0,时为正类。当W*X+b*<0时,为负类。
2、感知机算法
对于二分类问题,假设有m个训练样本{(X(1),y(1)),(X(2),y(2)),.......,(X(m),y(m))}其中,y∈{-1,1}。那么,应该如何从训练中的到分隔超平面W*X+b*=0?
在感知机算法中直接使用通误分类的样本到分隔超平面之间的距离作为其损失函数,并利用梯度下降法求得误分类函数额极小值,得到最终的分隔超平面。
设直线 L 的方程为Ax+By+C=0,点 P 的坐标为(Xo,Yo),则点 P 到直线 L 的距离为:

对于训练样本点X(i),其到分隔超平面的距离S为:
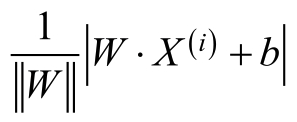
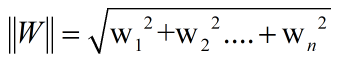
其中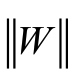 为W的L2范数,样本点X(i)到分隔超平面的距离S如图:
为W的L2范数,样本点X(i)到分隔超平面的距离S如图:

在训练样本中,对于误分类的样本(X(1),y(1)),即预测值WX(i)+b与真实值y(i)异号,即:
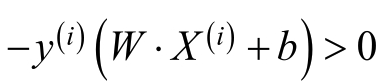
则误分类样本到分隔超平面之间的距离为:

若不考虑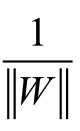 ,即为感知机算法的损失函数,感知机算法的损失函数为:
,即为感知机算法的损失函数,感知机算法的损失函数为:

通过求感知机损失函数的最小值 求得最终的分隔超平面。
求得最终的分隔超平面。
2.1、感知机算法存在的问题
在感知机算法中,通过最小化误分类样本到分隔超平面的距离,求得最终的分隔超平面,但是对于感知机算法来说,分隔超平面参数W和b的初始值和选择误分类样本的顺序对最终的分隔超平面的计算都有影响,采用不同的初始化值或者不同的误分类点,最终的分隔超平面是不同的,如下图可以分隔除不同的超平面:
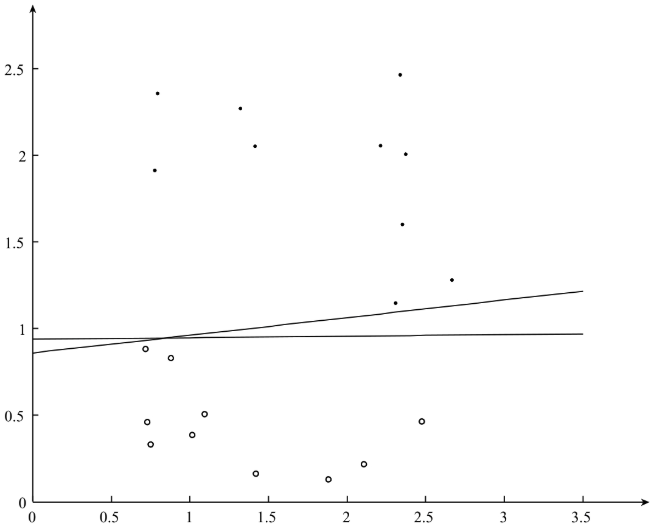
在图中的两个分隔超平面都能将正负样本区分开,对于感知机模型,采用不同的初始值或者不同的误分类点,最终的分隔超平面不同,在这些分隔超平面中是否存在一个最好的分隔超平面?
2.2、函数间隔和几何间隔
一般来讲,一个样本点距离分隔超平面的远近可以表示分类预测的确信度,在下图中样本点A离分隔超平面最远,若预测其为正类,就比较确信该预测是正确的;而样本点C离分隔超平面最远,若预测其为正类,就不是那么确信。为了能过表示分类预测的确信程度,我们分别定义函数间隔

函数间隔:
在感知机模型中,我们注意到分隔超平面W*X+b确定的情况下, 可以相对地表示样本点X(i)距离分隔超平面的远近,而当预测W*X(i)+b和样本标签y(i)同号时,表明最终分类是正确的,因此,可以使用y(i)*(W*X(i)+b)来表示分类的正确性和确信度,这便是函数间隔的定义。
可以相对地表示样本点X(i)距离分隔超平面的远近,而当预测W*X(i)+b和样本标签y(i)同号时,表明最终分类是正确的,因此,可以使用y(i)*(W*X(i)+b)来表示分类的正确性和确信度,这便是函数间隔的定义。
对于给定额训练集{(X(1),y(1)),(X(2),y(2)),.......,(X(m),y(m))}和分隔超平面,定义隔超平面关于样本点(X(i),y(i))的函数间隔为:
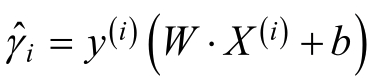
同时,定义分隔超平面关于训练数据集的函数为分隔超平面关于训练集中所有样本点的函数间隔的最小值:
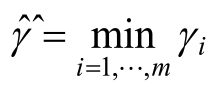
函数间隔可以表示分类预测的正确性和确定性。但是,在分隔超平面,如果其参数W和b同时扩大为原来点额2倍,这对于分隔超平面来说,并没有任何改变,但是对于函数间隔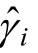 来说,即扩大为原来的2倍。为了解决这个问题,我们引入几何间隔。
来说,即扩大为原来的2倍。为了解决这个问题,我们引入几何间隔。
几何间隔:
为了能够使得间隔是一个确定值,可以对非分隔超平面的参数W加上默写约束,如归一化 。在上面的图中,对于样本X(i),其到分隔超平面之间的距离S为:
。在上面的图中,对于样本X(i),其到分隔超平面之间的距离S为:
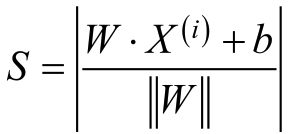
而当W*X(i)+b和样本标签y(i)同号时,表示预测正确,则样本X(i)到分隔超平面之间的距离S可以表示为:
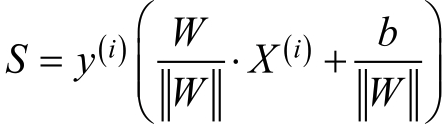
这便是几何间隔的定义。
对于给定的训练集{(X(1),y(1)),(X(2),y(2)),.......,(X(m),y(m))}和分隔超平面,定义分隔超平面关于样本点(X(i),y(i))的几何间隔为:
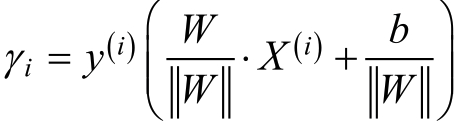
同时,定义分隔超平面关于训练数据集的几何间隔为分隔超平面关于训练集中所有样本点的几何间隔的最小值:

从上面的定义不难发现,几何间隔其实就是样本到分隔超平面的距离,对于几何间隔和函数间隔,有如下关系:
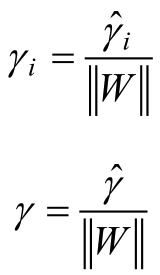
3、支持向量机
与感知机算法不同,在支持向量机(Support Vector Machines,SVM)中,求解出的分隔超平面不仅能够正确的划分训练数据集,而且几何间隔最大。
1、间隔最大化
对于几何间隔最大的分隔超平面:
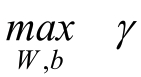
同时,对于每一个样本,需要满足:
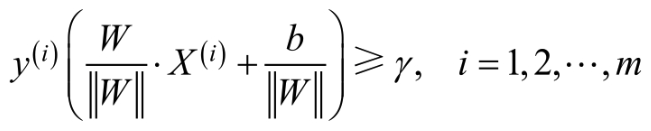
考虑到几何间隔和函数间隔之间的关系,则上述的几何间隔最大的分隔超平面可以等价为:
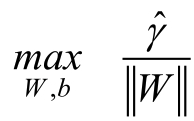

在函数间隔中,函数间隔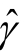 的取值并不影响到最优问题的解,如上所述,当参数W和b同时扩大为原来的2倍。函数间隔
的取值并不影响到最优问题的解,如上所述,当参数W和b同时扩大为原来的2倍。函数间隔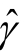 也会同时扩大为原来的2倍,这对于上述的优化问题和约束条件并没有影响,因此,可以取
也会同时扩大为原来的2倍,这对于上述的优化问题和约束条件并没有影响,因此,可以取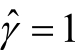 ,显然,为了最大化间隔,仅需最大化
,显然,为了最大化间隔,仅需最大化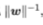 ,这等价于最小化
,这等价于最小化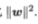 则上述问题变为:
则上述问题变为:
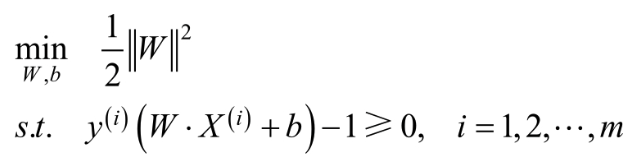
2、支持向量和间隔边界
对于上图中所示的线性可分的二分类问题,在m个训练样本中,与分隔超平面距离最近的样本称为支持向量(Support Vector)。支持向量对应的约束条件为;

当y(i)=+1时,支持向量所在的超平面为:
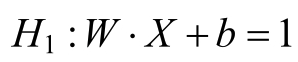
当y(i)=-1时,支持向量所在的超平面为:
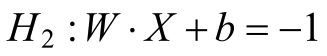
对于支持向量所在的超平面H1和H2 ,如图所示:

在图中,超平面H1和超平面H2之间的距离成为间隔,超平面H1和超平面H2又称为间隔边界,在确定最终的分隔超平面时,只有支持向量在起作用,其他的样本点并没有起到作用,由于支持向量在确定分隔超平面中起着重要的作用,因此,在这种分类模型被称支持向量机。
3、线性支持向量机
在上图所示的数据集中,其条件极为苛刻,要求所有的样本点都是线性可分的,即存在分隔超平面,能够将所有的则正样本正确的区分开,但是 实际情况中数据集很难满足这个条件,对于一个数据集,其中存在部分特异点,但是将这些特异点去除后,剩下的大部分样本定组成的集合线性可分的。
对于线性不可分的某些样本点(X(i),y(i))意味着其不能满足函数间隔最大于或等于1的约束条件,为了解决这个问题,可以对每个样本点(X(i),y(i))引进一个松弛变量ζi>=0,使得函数间隔加上松弛变量大于或等于1,这样,约束条件变为:
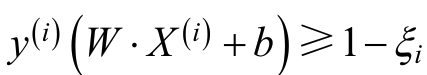
同时,对每个松弛变量ζi,支付一个代价C,此时,目标函数变为:

此时的优化目标为:

4、支持向量机的训练
通过以上问题的分析,我们可以知道,在SVM中。对分隔超平面的求解转化为对如下带有约束的最小化问题的求解:

对于带约束的优化问题,可以使用拉格朗日乘数法,将其转化为无约束优化问题的求解。对于上述的带约束的优化问题,可以转化成如下拉格朗日函数:

其中,α=(α1,α2,.......,αm),β=(β1,β2,......βm),且αi≧0,βi≧0,向量α,β称为拉格朗日乘子向量.上述的最小优化问题即为:

根据拉格朗日对偶性,原始问题的对偶问题为:

先求 ,在对拉格朗日函数L(W,b,ζ,α,β)中的W,b和ζ求偏导,并令其为0.
,在对拉格朗日函数L(W,b,ζ,α,β)中的W,b和ζ求偏导,并令其为0.
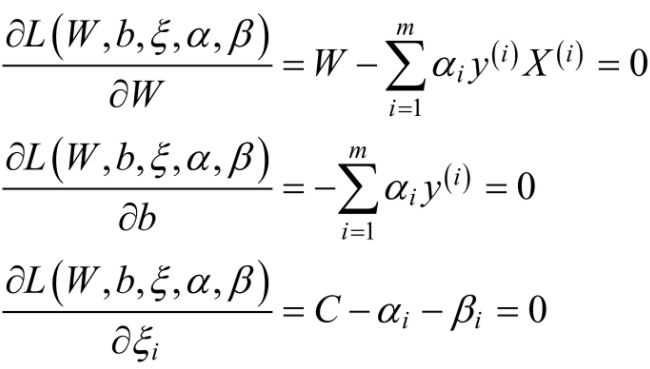
化简得:
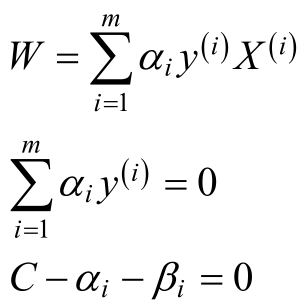
将上述代入到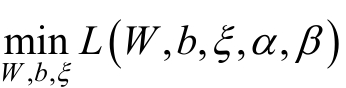 中,得到:
中,得到:
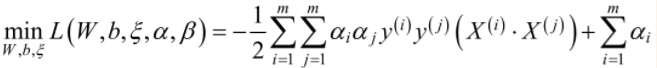
在对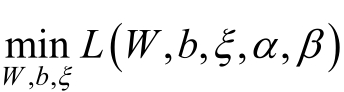 求α的极大,即的对偶问题:
求α的极大,即的对偶问题:

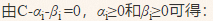

同时,将求解最大化问题,转化为求解最小化问题,则上述优化问题转化为:

当α*为上述对偶问题的最优解是,根据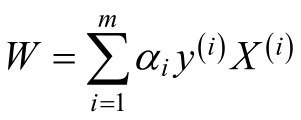 可以求得原始问题的最优解:
可以求得原始问题的最优解:
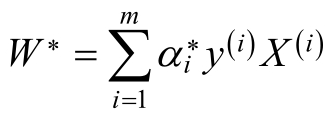
对于b的最优解b*,选择α*的一个分量α*j,其中α*j满足: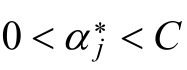
b*为:

由线性支持向量机到非线性支持向量机
对于一个非线性可分的问题,可以采用核函数的方式将非线性问题转化为线性问题,这里使用高斯核函数:

对于非线性支持向量机,此时的优化目标为:
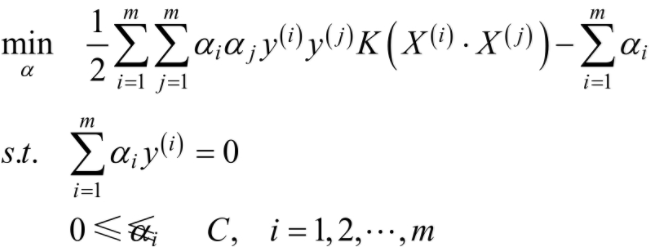
4.1、支持向量机(SVM)的更多相关文章
- 【IUML】支持向量机SVM
从1995年Vapnik等人提出一种机器学习的新方法支持向量机(SVM)之后,支持向量机成为继人工神经网络之后又一研究热点,国内外研究都很多.支持向量机方法是建立在统计学习理论的VC维理论和结构风险最 ...
- 机器学习:Python中如何使用支持向量机(SVM)算法
(简单介绍一下支持向量机,详细介绍尤其是算法过程可以查阅其他资) 在机器学习领域,支持向量机SVM(Support Vector Machine)是一个有监督的学习模型,通常用来进行模式识别.分类(异 ...
- 以图像分割为例浅谈支持向量机(SVM)
1. 什么是支持向量机? 在机器学习中,分类问题是一种非常常见也非常重要的问题.常见的分类方法有决策树.聚类方法.贝叶斯分类等等.举一个常见的分类的例子.如下图1所示,在平面直角坐标系中,有一些点 ...
- 机器学习算法 - 支持向量机SVM
在上两节中,我们讲解了机器学习的决策树和k-近邻算法,本节我们讲解另外一种分类算法:支持向量机SVM. SVM是迄今为止最好使用的分类器之一,它可以不加修改即可直接使用,从而得到低错误率的结果. [案 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 支持向量机SVM——专治线性不可分
SVM原理 线性可分与线性不可分 线性可分 线性不可分-------[无论用哪条直线都无法将女生情绪正确分类] SVM的核函数可以帮助我们: 假设‘开心’是轻飘飘的,“不开心”是沉重的 将三维视图还原 ...
- 一步步教你轻松学支持向量机SVM算法之案例篇2
一步步教你轻松学支持向量机SVM算法之案例篇2 (白宁超 2018年10月22日10:09:07) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- 一步步教你轻松学支持向量机SVM算法之理论篇1
一步步教你轻松学支持向量机SVM算法之理论篇1 (白宁超 2018年10月22日10:03:35) 摘要:支持向量机即SVM(Support Vector Machine) ,是一种监督学习算法,属于 ...
- OpenCV 学习笔记 07 支持向量机SVM(flag)
1 SVM 基本概念 本章节主要从文字层面来概括性理解 SVM. 支持向量机(support vector machine,简SVM)是二类分类模型. 在机器学习中,它在分类与回归分析中分析数据的监督 ...
- OpenCV支持向量机(SVM)介绍
支持向量机(SVM)介绍 目标 本文档尝试解答如下问题: 如何使用OpenCV函数 CvSVM::train 训练一个SVM分类器, 以及用 CvSVM::predict 测试训练结果. 什么是支持向 ...
随机推荐
- windows下怎么安装protobuf for python
首先从google上下载protobuf-3.0.0.zip和protoc-3.0.0-win32.zip,然后把protoc-3.0.0-win32.zip里的protoc.exe放到protobu ...
- 面向对象的JavaScript-008-Function介绍
1. // 函数 /* Declare the function 'myFunc' */ function myFunc(theObject) { theObject.brand = "To ...
- Python 解析配置模块之ConfigParser详解-乾颐堂
1.基本的读取配置文件 -read(filename) 直接读取ini文件内容 -sections() 得到所有的section,并以列表的形式返回 -options(section) 得到该sect ...
- VMware联网问题
VMware 服务启动优化当虚拟机连不上网,或不显示ip时,先查看vm服务是否启动.控制台运行:services.msc 以下为改为手工启动:1.VMware 服务自动启动影响计算机启动速度,再此对V ...
- Photo1
Story: 想象你是一个乡村的孩子,你有着健康的肤色,正在和家人一起坐在颠簸的马车上,赶着去城里买东西.正值夏日,黄昏的阳光晒在你的脸上,于是你的脸显得红扑扑的.路上满满的都是葱绿的草和参差不齐的树 ...
- 1146 ID Codes
题目链接: http://poj.org/problem?id=1146 题意: 给定一个字符串(长度不超过50), 求这个字符串的下一个字典序的字符串, 如果已经是最大字典序, 那么输出 " ...
- centos7部署JavaWeb项目
centos7部署JavaWeb项目共有三步 1.配置java环境 2.配置tomcat环境. 3.部署JavaWeb项目 一.配置java环境 1.1安装java 参考我的另一篇博文:https:/ ...
- UVa 11324 The Largest Clique (强连通分量+DP)
题意:给定一个有向图,求一个最大的结点集,使得任意两个结点,要么 u 能到 v,要么 v 到u. 析:首先,如果是同一个连通分量,那么要么全选,要么全不选,然后我们就可以先把强连通分量先求出来,然后缩 ...
- 编写高质量代码改善C#程序的157个建议——建议69:应使用finally避免资源泄漏
建议69:应使用finally避免资源泄漏 除非发生让应用程序中断的异常,否则finally总是会先于return执行.finally的这个语言特性决定了资源释放的最佳位置就是在finally块中:另 ...
- 【图解HTTP】第二章 简单的http协议
简单的HTTP协议 针对HTTP协议结构进行讲解,主要使用HTTP/1.1版本. HTTP协议用于客户端和服务器端之间的通信 通过请求和响应的交换达成通信(从客户端开始建立通信,服务器端在没有接收到请 ...
