【BZOJ 1923】1923: [Sdoi2010]外星千足虫 （高斯消元异或 | BITSET用法）

1923: [Sdoi2010]外星千足虫

Description

Input

第一行是两个正整数 N, M。 接下来 M行，按顺序给出 Charles 这M次使用“点足机”的统计结果。每行 包含一个“01”串和一个数字，用一个空格隔开。“01”串按位依次表示每只虫 子是否被放入机器：如果第 i 个字符是“0”则代表编号为 i 的虫子未被放入，“1” 则代表已被放入。后面跟的数字是统计的昆虫足数 mod 2 的结果。 由于 NASA的实验机器精确无误，保证前后数据不会自相矛盾。即给定数据 一定有解。

Output

在给定数据存在唯一解时有 N＋1行，第一行输出一个不 超过M的正整数K，表明在第K 次统计结束后就可以确定唯一解；接下来 N 行 依次回答每只千足虫的身份，若是奇数条足则输出“?y7M#”（火星文），偶数 条足输出“Earth”。如果输入数据存在多解，输出“Cannot Determine”。 所有输出均不含引号，输出时请注意大小写。

Sample Input

3 5
011 1
110 1
101 0
111 1
010 1

Sample Output

4
Earth
?y7M#
Earth

HINT

对于 20%的数据，满足 N＝M≤20； 
对于 40%的数据，满足 N＝M≤500； 
对于 70%的数据，满足 N≤500，M≤1,000； 
对于 100%的数据，满足 N≤1,000，M≤2,000。

==========================================================
请不要提交!

Source

第一轮Day1

【分析】

　　这题很明显是高斯消元。

　　但是直接做，额。。n^3？。。但是其实每个数都只是0和1并且是异或操作。

　　然后看到大神们都用bitset。。表示不会于是抄了一下。。。【后面总结bitset用法

　　可能这个当成一个数操作比较快吧。

　　然后高斯消元那里，我是一个个动态插入那种的，最后异或到每个有效方程都只是有一个1。【解就很容易输出了耶

　　一开始我还以为是个异或方程组，其实能异或是因为他的运算实际上就是加法mod2，即异或。

　　好了差不多了，放代码。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #include<bitset>
 using namespace std;
 #define Maxn 1010
 #define Maxm 2010
 
 bitset<Maxn> a[Maxm];
 char s[Maxn];
 int n,m,id[Maxn],nw;
 
 void add(int x)
 {
     int k=;
     for(int i=;i<=n;i++) if(a[x][i])
     {
         if(id[i]||k) a[x]^=a[id[i]];
         else
         {
             id[i]=x;k=i;
         }
     }
     if(k)
     {
         nw++;
         for(int i=;i<=n;i++) if(i!=k&&id[i]&&a[id[i]][k])
         {
             a[id[i]]^=a[x];
         }
     }
 }
 
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
     {
         scanf("%s",s+);
         for(int j=;j<=n;j++) a[i][j]=s[j]-'';
         int x;
         scanf("%d",&x);
         a[i][n+]=x;
     }
     nw=;
     memset(id,,sizeof(id));
     int ok=;
     for(int i=;i<=m;i++)
     {
         add(i);
         if(nw==n) {ok=i;break;}
     }
     if(ok==) printf("Cannot Determine\n");
     else
     {
         printf("%d\n",ok);
         for(int i=;i<=n;i++)
         {
             if(a[id[i]][n+]==) printf("Earth\n");
             else printf("?y7M#\n");
         }
     }
     return ;
 }

2017-03-23 09:38:20

---

---

　　BITSET 总结

ACM的奇计淫巧_bitset优化

什么是bitset

bitset 是STL库中的二进制容器，根据C++ reference 的说法，bitset可以看作bool数组，但优化了空间复杂度和时间复杂度，并且可以像整形一样按位与或。

使用方法

申明

bitset的申明要指明长度

bitset<length> bi

这样就申明了一个长度为length的名叫bi的bitset

赋值

bitset重载了[]运算符，故可以像bool数组那样赋值

bi[2] = 1;

这样就能将第二位赋值为1

常用函数

b1 = b2 & b3;//按位与
b1 = b2 | b3;//按位或
b1 = b2 ^ b3;//按位异或
b1 = ~b2;//按位补
b1 = b2 << 3;//移位

int one = b1.count();//统计1的个数

优化作用

常常碰到处理的数组只有0和1的变化，此时就可以使用bitset优化。比如求两个集合的交集可以使用按位与运算，求并集可以使用按位或运算

来自：http://www.cnblogs.com/HarryGuo2012/p/4712245.html

 

认识C++中的bitset类型

认识标准库bitset类型

位是用来保存一组项或者条件的yes/no（1或者0）信息的一种简洁方法，那么位集就是二进制位的有序集。C++中标准库提供的bitset类在我们程序中就很有效的简化了对于位集的处理。

bitset对象的定义

我们要使用bitset，首先需要包含头文件bitset。和vector对象不一样的是bitset类型对象的区别仅在其长度而不在其类型。在定义bitset的时候，要明确bitset包含了多少位，须在尖括号内给出它的长度值。长度值必须定义为整形字面值常量或是已用常量值初始化的整型的const对象。

1 const int maxn=16;
2 bitset<32> bitvec2;
3 bitset<maxn> bitvec(1);

bitset中以0位开始的位串是低阶位，以31位结束的位串是高阶位。

bitset对象的初始化

1.用unsigned值初始化

当用unsigned long值作为bitset对象的初始值时，该值将转化为二进制的位模式。而bitset对象中的位集作为这种位模式的副本。如果bitset类型长度大于unsigned long的值的二进制位数，则其余的高阶位将置为0；如果bitset类型长度小于unsigned long值的二进制位数，则只使用unsigned值中的低阶位，超过bitset类型长度的高阶位将被丢弃。

1 bitset<32> bitvec3(0xffff);
2 cout<<bitvec3<<endl;
3 for (int i=0 ; i<bitvec3.size() ; i++)
4     cout<<bitvec3[i]<<" ";
5 cout<<endl;

2.用string对象初始化bitset对象

当用string对象初始化bitset对象时，string对象直接表示为位模式。从string对象读入位集的顺序是从右往左。

1 string str("11100");
2 bitset<8> bitvec5(str);
3 cout<<bitvec5<<endl;
4 for (int i=0 ; i<bitvec5.size() ; i++)
5     cout<<bitvec5[i]<<" ";

注意：string对象和bitset对象之间是反向转化的，string对象的最右边字符（即下标最大的那个字符）用来初始化bitset对象的低阶位（即下标为0的位）。

访问bitset对象中的位

和 vector一样，bitset也可以通过下标操作符来读写某个索引位置的二进制位，同样的，也可以用下标操作符来测试给定二进制位的值或者设置某个二进 制位的值。其实访问bitset对象中的位就是一个for循环即可搞定，上文代码插图中就有提到，这里就不作详细介绍了。

bitset操作函数

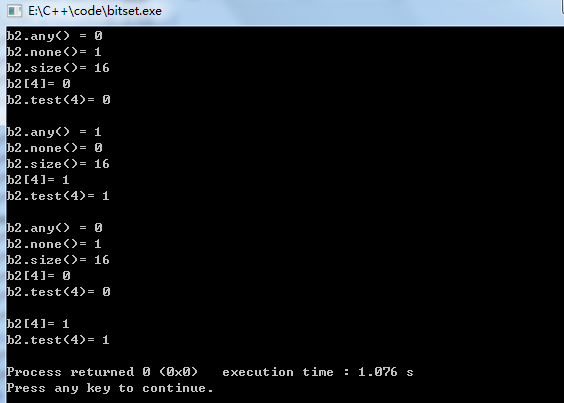
bitset操作函数具体实现

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<bitset>
using namespace std;
const int maxn=16;
 
int main()
{
    bitset<16> b2;
    cout<<"b2.any() = "<<b2.any()<<endl;
    cout<<"b2.none()= "<<b2.none()<<endl;
    cout<<"b2.size()= "<<b2.size()<<endl;
    cout<<"b2[4]= "<<b2[4]<<endl;
    cout<<"b2.test(4)= "<<b2.test(4)<<endl;
    b2.set() ; cout<<endl;
    cout<<"b2.any() = "<<b2.any()<<endl;
    cout<<"b2.none()= "<<b2.none()<<endl;
    cout<<"b2.size()= "<<b2.size()<<endl;
    cout<<"b2[4]= "<<b2[4]<<endl;
    cout<<"b2.test(4)= "<<b2.test(4)<<endl;
    b2.reset() ; cout<<endl;
    cout<<"b2.any() = "<<b2.any()<<endl;
    cout<<"b2.none()= "<<b2.none()<<endl;
    cout<<"b2.size()= "<<b2.size()<<endl;
    cout<<"b2[4]= "<<b2[4]<<endl;
    cout<<"b2.test(4)= "<<b2.test(4)<<endl;
    b2.set(4) ; cout<<endl;
    cout<<"b2[4]= "<<b2[4]<<endl;
    cout<<"b2.test(4)= "<<b2.test(4)<<endl;
    return 0;
}

来自:http://www.cnblogs.com/BaiYiShaoNian/p/4591167.html