【算法】矩阵填数,深度优先搜索(DFS),Pascal改C语言
面向对象的上机实验
题目
以下列方式向 5*5 矩阵中填入数字。设数字i(1=<i<=25),则数字i+1 的坐标位置应为(E, W)。(E, W)可根据下列关系由(x,y)算出:
1)(E, W)=(x±3,y)
2)(E, W)=(x,y±3)
3)(E, W)=(x±2,y±2)
求解问题如下:
编写一个程序,当数字1被指定于某个起始位置时,列举出其它24个数字应在的位置;列举该条件下的所有可能方案。
参考答案
网上搜索到数学奥赛中本题的Pascal代码
来自http://blog.sina.com.cn/s/blog_1317189490102vp1k.html
Program lx9__;
uses crt;
const n=;
d:array[..,..] of shortint=((,),(-,),(,),(,-),
(,),(,-),(-,),(-,-));
var x0,y0:byte;
a:array[..n,..n] of byte;
total:longint; procedure print;
var i,j:integer;
begin
inc(total);
gotoxy(,);
writeln('[',total,']');
for i:= to n do
begin
for j:= to n do
write(a[i,j]:);
writeln;
end;
end; procedure try(x,y,k:byte);
var i,x1,y1:integer;
begin
for i:= to do
begin
x1:=x+d[i,];y1:=y+d[i,];
if (x1>) and (y1>) and (x1<=n)
and (y1<=n) and (a[x1,y1]=) then
begin
a[x1,y1]:=k;
if k=n*n then print
else try(x1,y1,k+);
a[x1,y1]:=;
end;
end;
end; begin
clrscr;
write('x0,y0=');readln(x0,y0);
fillchar(a,sizeof(a),);
total:=;a[x0,y0]:=;
try(x0,y0,);
writeln('Total=',total);
writeln('Press any key to exit..。');
repeat until keypressed;
end.
自改C语言代码
运用了深度优先搜索算法。
可以输入一个起始位置的坐标后,列举出所有可能方案和方案个数。
也可以输出所有初始点方案的个数。
#include <stdio.h>
#define N 5//格子行列数 int next[][]={{,},{-,},{,},{,-},{,},{,-},{-,},{-,-}};//下一步变换的位移
int x0,y0;//输入的初始坐标
int matrix[N][N];//存储nxn矩阵中的数字
int total;//方案数量 //打印一个矩阵的函数
void printMatrix(){
int i,j;
total+=;//出来一次结果,就打印一次,方案数+1
printf("第%d种方案:\n",total);
for(i=;i<N;i++){
for(j=;j<N;j++){
printf("%4d",matrix[i][j]);//%4d表示输出宽度为4,且右对齐
}
printf("\n");
}
printf("\n");
}
////每个初始点都输出方案的个数的话就不把每个方案打印出来了,太占地方
//void printMatrix(){
// int i,j;
// total+=1;//出来一次结果,就打印一次,方案+1
//} //主要函数,(x,y)是矩阵内坐标,k是第几个数字
void try(x,y,k){
int i,x1,y1;//x1,y1是本次要找的坐标
//将8个位移都试一遍
for(i=;i<;i++){
x1=x+next[i][];
y1=y+next[i][];
//如果该位置不超过边界且没有数字,则方案可行,把数字装进这个位置
if((x1>-)&&(y1>-)&&(x1<N)&&(y1<N)&&(matrix[x1][y1]==)){
matrix[x1][y1]=k;
//如果k=25即已经搜索完,可以打印了
if(k==N*N)
printMatrix();
//如果还没到25,就继续搜索下一个位置
else
try(x1,y1,k+);
//本次打印完/本次搜索尝试到死路,回溯到上一节点去往另一分支前,将这一节点清零
matrix[x1][y1]=;
}
}
} int main()
{
//输入坐标
printf("请输入第一个数的坐标(逗号间隔):");
scanf("%d,%d",&x0,&y0); //矩阵整体清0(第一条在dev-c++可以跑,vc++不行,还是用老办法)
//memset(matrix, 0, sizeof(matrix));
int i,j;
for(i=;i<N;i++){
for(j=;j<N;j++){
matrix[i][j]=;
}
} //数据初始化,运行
total=;//方案数为零
x0-=;y0-=;//用户输入坐标从1开始,c语言数组从0开始
matrix[x0][y0]=;//第一个位置赋值1
try(x0,y0,); //从数字2开始放置 printf("总共有%d种摆放方案\n\n",total); // //每个初始点都输出方案的个数
// int m,n;
// for(m=0;m<5;m++){
// for(n=0;n<5;n++){
// x0=m;y0=n;
// //矩阵整体清0
// int i,j;
// for(i=0;i<N;i++){
// for(j=0;j<N;j++){
// matrix[i][j]=0;
// }
// }
// total=0;//每次节点前方案数清零
// matrix[x0][y0]=1;//第一个位置赋值1
// try(x0,y0,2); //从数字2开始放置
// printf("数字1被指定于(%d,%d)有%d种方案\n",m+1,n+1,total);
// }
// printf("\n");//每5行之后打个空行好看点
// }
}
结果
- 输入一个起始点坐标后输出的方案

- 输出所有起始点的方案个数:
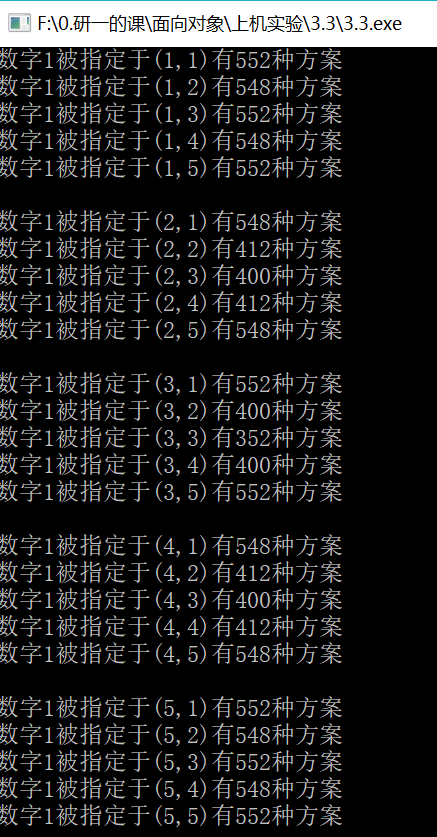
【算法】矩阵填数,深度优先搜索(DFS),Pascal改C语言的更多相关文章
- 算法与数据结构基础 - 深度优先搜索(DFS)
DFS基础 深度优先搜索(Depth First Search)是一种搜索思路,相比广度优先搜索(BFS),DFS对每一个分枝路径深入到不能再深入为止,其应用于树/图的遍历.嵌套关系处理.回溯等,可以 ...
- 【算法入门】深度优先搜索(DFS)
深度优先搜索(DFS) [算法入门] 1.前言深度优先搜索(缩写DFS)有点类似广度优先搜索,也是对一个连通图进行遍历的算法.它的思想是从一个顶点V0开始,沿着一条路一直走到底,如果发现不能到达目标解 ...
- 深度优先搜索 DFS 学习笔记
深度优先搜索 学习笔记 引入 深度优先搜索 DFS 是图论中最基础,最重要的算法之一.DFS 是一种盲目搜寻法,也就是在每个点 \(u\) 上,任选一条边 DFS,直到回溯到 \(u\) 时才选择别的 ...
- 深度优先搜索DFS和广度优先搜索BFS简单解析(新手向)
深度优先搜索DFS和广度优先搜索BFS简单解析 与树的遍历类似,图的遍历要求从某一点出发,每个点仅被访问一次,这个过程就是图的遍历.图的遍历常用的有深度优先搜索和广度优先搜索,这两者对于有向图和无向图 ...
- 深度优先搜索DFS和广度优先搜索BFS简单解析
转自:https://www.cnblogs.com/FZfangzheng/p/8529132.html 深度优先搜索DFS和广度优先搜索BFS简单解析 与树的遍历类似,图的遍历要求从某一点出发,每 ...
- 利用广度优先搜索(BFS)与深度优先搜索(DFS)实现岛屿个数的问题(java)
需要说明一点,要成功运行本贴代码,需要重新复制我第一篇随笔<简单的循环队列>代码(版本有更新). 进入今天的主题. 今天这篇文章主要探讨广度优先搜索(BFS)结合队列和深度优先搜索(DFS ...
- [FJOI2017]矩阵填数——容斥
参考:题解 P3813 [[FJOI2017]矩阵填数] 题目大意: 给定一个 h∗w 的矩阵,矩阵的行编号从上到下依次为 1...h ,列编号从左到右依次 1...w . 在这个矩阵中你需要在每个格 ...
- P3813 [FJOI2017]矩阵填数(组合数学)
P3813 [FJOI2017]矩阵填数 shadowice1984说:看到计数想容斥........ 这题中,我们把图分成若干块,每块的最大值域不同 蓝后根据乘法原理把每块的方案数(互不相干)相乘. ...
- bzoj5010: [Fjoi2017]矩阵填数
Description 给定一个 h*w 的矩阵,矩阵的行编号从上到下依次为 1..h,列编号从左到右依次1..w.在这个矩阵中你需要在每 个格子中填入 1..m 中的某个数.给这个矩阵填数的时候有一 ...
- [BZOJ5010][FJOI2017]矩阵填数(状压DP)
5010: [Fjoi2017]矩阵填数 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 90 Solved: 45[Submit][Status][ ...
随机推荐
- open_window()到底做了什么?
Hlong MainWndID= (Hlong)m_hWnd; open_framegrabber(, , , , , , , , "default", , -, &Acq ...
- web上传下载文件
WebService代码: /// /// 上传文件 /// /// 文件的byte[] /// 上传文件的路径 /// 上传文件名字 /// ...
- C语言学习系列(六)存储类
一.C存储类 存储类定义C程序中变量/函数的范围(可见性)和生命周期.这些说明符放置在他们所修饰的类型之前.for example:auto.register.static.extern. (一).a ...
- 002_linux之点灯(汇编深度解析)
1. 开发板采用韦山东的开发板 2. 芯片CPU三星S3C2440A 3. 控制引脚:GPF4 4. linux操作系统 5. 芯片手册下载地址:https://eyun.ba ...
- WSDL的学习
1.WSDL是什么? 2.wsdl说明书结构 拿到说明书,从下往上看, 图2-1 port:为端点 binding:绑定 图2-2 type属性----->找到portType标签 operat ...
- Django-中间件实现1分钟内只允许三次访问
代码 class Throttle(MiddlewareMixin): def process_request(self, request): # 1. 拿到用户请求的IP # print(reque ...
- sequence_loss的解释
在做seq2seq的时候,经常需要使用sequence_loss这是损失函数. 现在分析一下sequence_loss这个函数到底在做什么 # coding: utf-8 import numpy a ...
- c++ 数据类型长度
#include <iostream> using namespace std; int main() { cout << "char: " << ...
- MongoDB-查询关键字/排序等
查询关键字 并列查询$and # 条件都成立才可以查询到结果 db.stutent.find({$and:[{name:"小漩涡"},{age:30}]}) 或查询$or # 有一 ...
- CentOS 7.5 ——如何开放80、8080、3306等端口
CentOS 7.5 ——如何开放80.8080.3306等端口 ——说明:CentOS 7.0默认使用的是firewall作为防火墙,这里改为iptables防火墙——1.关闭firewall: s ...
