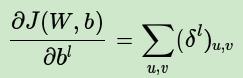CNN中卷积层 池化层反向传播
参考:https://blog.csdn.net/kyang624823/article/details/78633897
卷积层 池化层反向传播:
1,CNN的前向传播
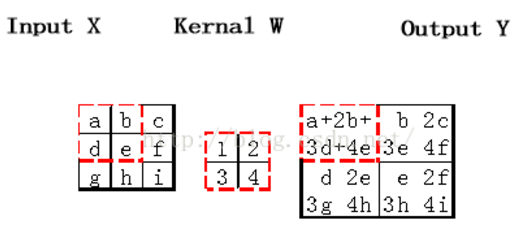
a)对于卷积层,卷积核与输入矩阵对应位置求积再求和,作为输出矩阵对应位置的值。如果输入矩阵inputX为M*N大小,卷积核为a*b大小,那么输出Y为(M-a+1)*(N-b+1)大小。
b)对于池化层,按照池化标准把输入张量缩小。
c)对于全连接层,按照普通网络的前向传播计算。
2,CNN反向传播的不同之处:
首先要注意的是,一般神经网络中每一层输入输出a,z都只是一个向量,而CNN中的a,z是一个三维张量,即由若干个输入的子矩阵组成。其次:
- 池化层没有激活函数。这个问题倒比较好解决,我们可以令池化层的激活函数为σ(z)=z,即激活后就是自己本身。这样池化层激活函数的导数为1。
- 池化层在前向传播的时候,对输入进行了压缩,那么我们向前反向推导上一层的误差时,需要做upsample处理。
- 卷积层是通过张量卷积,或者说若干个矩阵卷积求和而得到当前层的输出,这和一般的网络直接进行矩阵乘法得到当前层的输出不同。这样在卷积层反向传播的时候,上一层误差的递推计算方法肯定有所不同。
- 对于卷积层,由于W使用的运算是卷积,那么由该层误差推导出该层的所有卷积核的W,b的方式也不同。
由于卷积层可以有多个卷积核,各个卷积核的处理方法是完全相同且独立的,为了简化算法公式的复杂度,我们下面提到卷积核都是卷积层中若干卷积核中的一个。接下来看具体的CNN反向传播步骤。
3,已知池化层的误差,反向推导上一隐藏层的误差
在前向传播时,池化层我们会用MAX或者Average对输入进行池化,池化的区域大小已知。现在我们反过来,要从缩小后区域的误差,还原前一层较大区域的误差。这个过程叫做upsample。假设我们的池化区域大小是2x2。第l层误差的第k个子矩阵为:
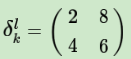
如果池化区域表示为a*a大小,那么我们把上述矩阵上下左右各扩展a-1行和列进行还原:
Pooling层反向传播需要保证传递的loss(或者梯度)总和不变。根据这条原则,mean pooling和max pooling的反向传播也是不同的。
MAX POOLING:
如果是MAX,假设我们之前在前向传播时记录的最大值位置分别是左上,右下,右上,左下,则转换后的矩阵为: 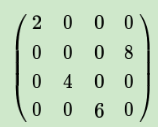
举个例子:
max pooling也要满足梯度之和不变的原则,max pooling的前向传播是把patch中最大的值传递给后一层,而其他像素的值直接被舍弃掉。那么反向传播也就是把梯度直接传给前一层某一个像素,而其他像素不接受梯度,也就是为0。所以max pooling操作和mean pooling操作不同点在于需要记录下池化操作时到底哪个像素的值是最大,也就是max id,这个变量就是记录最大值所在位置的,因为在反向传播中要用到,那么假设前向传播和反向传播的过程就如下图所示 :

Average POOLING
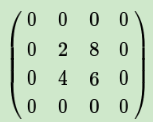
如果是Average,则进行平均,转换后的矩阵为:
举个例子:
mean pooling的前向传播就是把一个patch中的值求取平均来做pooling,那么反向传播的过程也就是把某个元素的梯度等分为n份分配给前一层,这样就保证池化前后的梯度(残差)之和保持不变
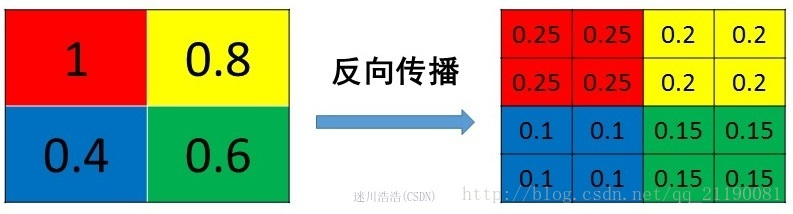
上边这个矩阵就是误差矩阵经过upsample之后的矩阵,那么,由后一层误差推导出前一层误差的公式为: 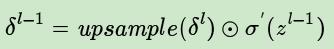
上式和普通网络的反向推导误差很类似: 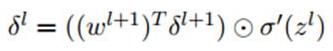
可以看到,只有第一项不同。
4,已知卷积层的误差,反向推导上一隐藏层的误差、
推导链接:https://blog.csdn.net/legend_hua/article/details/81590979
公式如下: 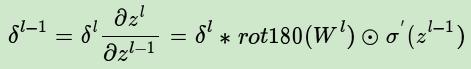
我们再看一次普通网络的反向推导误差的公式: 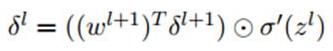
可以看到区别在于,下一层的权重w的转置操作,变成了旋转180度的操作,也就是上下翻转一次,左右再翻转一次,这其实就是“卷积”一词的意义(我们可简单理解为数学上的trick),可参考下图,Q是下一层的误差,周围补0方便计算,W是180度翻转后的卷积核,P是W和Q做卷积的结果:
5,已知卷积层的误差,推导该层的W,b的梯度
经过以上各步骤,我们已经算出每一层的误差了,那么:
a)对于全连接层,可以按照普通网络的反向传播算法求该层W,b的梯度。
b)对于池化层,它并没有W,b,也不用求W,b的梯度。
c)只有卷积层的W,b需要求出,先看w: 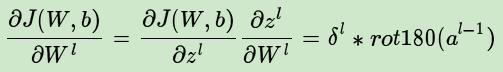
再对比一下普通网络的求w梯度的公式,发现区别在于,对前一层的输出做翻转180度的操作: 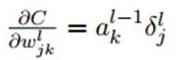
而对于b,则稍微有些特殊,因为在CNN中,误差δ是三维张量,而b只是一个向量,不能像普通网络中那样直接和误差δ相等。通常的做法是将误差δ的各个子矩阵的项分别求和,得到一个误差向量,即为b的梯度:
CNN中卷积层 池化层反向传播的更多相关文章
- Python3 CNN中卷积和池化的实现--限制为二维输入
# -*- coding: utf-8 -*- """ Created on Wed Jan 31 14:10:03 2018 @author: markli " ...
- tensorflow中的卷积和池化层(一)
在官方tutorial的帮助下,我们已经使用了最简单的CNN用于Mnist的问题,而其实在这个过程中,主要的问题在于如何设置CNN网络,这和Caffe等框架的原理是一样的,但是tf的设置似乎更加简洁. ...
- tensorflow的卷积和池化层(二):记实践之cifar10
在tensorflow中的卷积和池化层(一)和各种卷积类型Convolution这两篇博客中,主要讲解了卷积神经网络的核心层,同时也结合当下流行的Caffe和tf框架做了介绍,本篇博客将接着tenso ...
- CNN学习笔记:池化层
CNN学习笔记:池化层 池化 池化(Pooling)是卷积神经网络中另一个重要的概念,它实际上是一种形式的降采样.有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见 ...
- ubuntu之路——day17.3 简单的CNN和CNN的常用结构池化层
来看上图的简单CNN: 从39x39x3的原始图像 不填充且步长为1的情况下经过3x3的10个filter卷积后 得到了 37x37x10的数据 不填充且步长为2的情况下经过5x5的20个filter ...
- Tensorflow之CNN卷积层池化层padding规则
padding的规则 · padding=‘VALID’时,输出的宽度和高度的计算公式(下图gif为例) 输出宽度:output_width = (in_width-filter_wid ...
- 【DeepLearning】基本概念:卷积、池化、Backpropagation
终于有了2个月的空闲时间,给自己消化沉淀,希望别有太多的杂事打扰.在很多课程中,我都学过卷积.池化.dropout等基本内容,但目前在脑海中还都是零散的概念,缺乏整体性框架,本系列博客就希望进行一定的 ...
- 深度学习原理与框架-卷积神经网络基本原理 1.卷积层的前向传播 2.卷积参数共享 3. 卷积后的维度计算 4. max池化操作 5.卷积流程图 6.卷积层的反向传播 7.池化层的反向传播
卷积神经网络的应用:卷积神经网络使用卷积提取图像的特征来进行图像的分类和识别 分类 相似图像搜索 ...
- 第十三节,使用带有全局平均池化层的CNN对CIFAR10数据集分类
这里使用的数据集仍然是CIFAR-10,由于之前写过一篇使用AlexNet对CIFAR数据集进行分类的文章,已经详细介绍了这个数据集,当时我们是直接把这些图片的数据文件下载下来,然后使用pickle进 ...
随机推荐
- AGC032E modulo pairing
题意 原题 给出\(2n\)个\(\leq m\)的数,求最优的两两配对方案 使\(n\)组\((x,y)\)的\((x+y)mod \space m\)最大值最小 \(n\leq 10^5,m \l ...
- js反混淆
var esprima = require('esprima') var escodegen = require('escodegen') content = "function _0x35 ...
- LeetCode 124. 二叉树中的最大路径和(Binary Tree Maximum Path Sum)
题目描述 给定一个非空二叉树,返回其最大路径和. 本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列.该路径至少包含一个节点,且不一定经过根节点. 示例 1: 输入: [1,2,3] 1 ...
- Django admin site应用
django自带的admin后台管理,可以实现对数据库表的增删改查,用起来十分方便.其使用和配置主要分为三个步骤: 1,创建超级用户 需要创建超级用户来登陆admin后台系统,在命令行中输入 pyth ...
- Spring对象依赖关系
Spring中,如何给对象的属性赋值? [DI, 依赖注入] 1) 通过构造函数 2) 通过set方法给属性注入值 3) p名称空间 4)自动装配(了解) 5) 注解 package loade ...
- selenium 2019 笔记
1.get打开本地目录的方法
- Jmeter性能测试工具的使用(Web性能测试)
Jmeter性能测试工具的使用(Web性能测试) 1.下载 http://pan.baidu.com/s/1o7p18Ye 该软件不用安装,直接解压打开即可使用. 2.使用 这里就在win下进行,图形 ...
- 利用canvas对图片进行切割
使用input标签选择一张图片, 然后利用canvas对图片进行切割, 可以设置切割的行数和列数 这是html代码 ... <input type="file" id=&qu ...
- eNSP路由器输出 '#' 无法启动的一种解决方法
试过网上的改virtulboxIP.关防火墙.改兼容性等方法,都不成功.后来发现通过改变选择路由器的型号可以启动. 如果对路由器没有特殊需求,可以选择型号数字较小的试一下(最低可以选择Router).
- python-爬虫-scrapy
入门: 下载:pip install scrapy 工程:scrapy startproject 工程名 Spider: scrapy genspider 爬虫名 url (--nolog//可选不 ...