[JOI2012春季合宿]Constellation (凸包)

题意

题解

神仙结论题。

结论: 一个点集合法当且仅当其凸包上的两种颜色点分别连续。

证明:

必要性显然。

充分性: 考虑对于一个不同色三角形\(ABC\)，不妨设点\(A\)为白点，点\(B,C\)为黑点。若形内无白点，则随便连，显然成立。若形内有白点，则任取一白点\(S\), 对三角形\(SBC,BAS,CAS\)内部的点分别连边（递归构造），最后连接\(SA\).

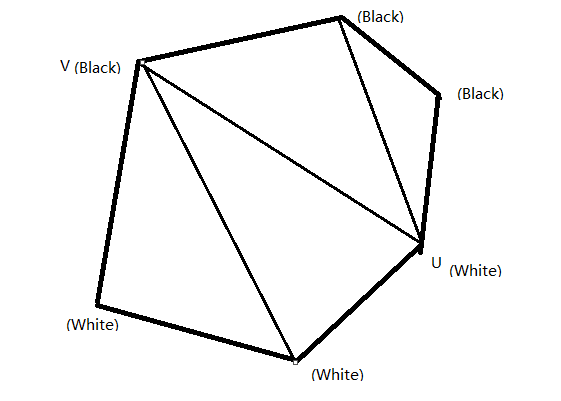
再考虑一个凸包，设在逆时针方向上最后一个白点是\(U\), 最后一个黑点是\(V\), 则连接\(UV\), 把凸包剖成两个部分，一部分只有\(V\)是黑，一部分只有\(U\)是白。然后进行如图所示三角剖分，每个三角形内连上即可。

知道了结论，这题就很简单了。

勿忘非空。

代码

#include<bits/stdc++.h>
#define llong long long
using namespace std;

const int N = 1e5;
const int P = 1e9+7;
struct Point
{
	llong x,y; int c,id;
	Point() {}
	Point(int _x,int _y) {x = _x,y = _y;}
} a[N+3],ch[N+3];
bool f[N+3];
Point operator -(Point x,Point y) {return Point(x.x-y.x,x.y-y.y);}
llong Cross(Point x,Point y) {return x.x*y.y-x.y*y.x;}
int n,sz;

bool cmp_ang(Point x,Point y) {return Cross(x-a[1],y-a[1])>0;}

int main()
{
	scanf("%d",&n);
	for(int i=1; i<=n; i++) scanf("%lld%lld%d",&a[i].x,&a[i].y,&a[i].c);
	for(int i=2; i<=n; i++) {if(a[i].x<a[1].x||(a[i].x==a[1].x&&a[i].y<a[1].y)) {swap(a[i],a[1]);}}
	sort(a+2,a+n+1,cmp_ang);
	for(int i=1; i<=n; i++) a[i].id = i;
	sz = 1; ch[1] = a[1];
	for(int i=2; i<=n; i++)
	{
		while(sz>=2 && Cross(ch[sz]-ch[sz-1],a[i]-ch[sz-1])<0) {sz--;}
		sz++; ch[sz] = a[i];
	}
//	printf("ch: "); for(int i=1; i<=sz; i++) printf("(%lld,%lld) ",ch[i].x,ch[i].y); puts("");
	int mx1 = 0,mn1 = n,mx2 = 0,mn2 = n; llong ans;
	for(int i=1; i<=sz; i++)
	{
		if(ch[i].c==1) {mx1 = max(mx1,i),mn1 = min(mn1,i);}
		else if(ch[i].c==2) {mx2 = max(mx2,i),mn2 = min(mn2,i);}
	}
//	printf("sz=%d mn1=%d mx1=%d mn2=%d mx2=%d\n",sz,mn1,mx1,mn2,mx2);
	if(mx1<mn1 && mx2<mn2)
	{
		ans = (1ll*sz*sz-sz+2ll)%P;
	}
	else if(mx1<mn1) //only 2
	{
		ans = 1ll;
		for(int i=mn2+1,j=0; i<=mn2+sz; i++)
		{
			int ii = i>sz?i-sz:i;
			if(ch[ii].c==0) {j++;}
			else {ans += 1ll*j*(j+1ll)/2ll; j = 0;}
		}
		ans %= P;
	}
	else if(mx2<mn2) //only 1
	{
		ans = 1ll;
		for(int i=mn1+1,j=0; i<=mn1+sz; i++)
		{
			int ii = i>sz?i-sz:i;
			if(ch[ii].c==0) {j++;}
			else {ans += 1ll*j*(j+1ll)/2ll; j = 0;}
		}
		ans %= P;
	}
	else
	{
		if(mn1>mn2)
		{
			for(int i=mn1; i<=mx1; i++)
			{
				if(ch[i].c==2) {puts("0"); return 0;}
			}
			int l = -1,r = -1;
			for(int i=mx1; ch[i].c!=2; i=(i==sz?1:i+1))
			{
				l++;
			}
			for(int i=mn1; ch[i].c!=2; i=(i==1?sz:i-1))
			{
				r++;
			}
			ans = 1ll*(l+1ll)*(r+1ll)%P;
		}
		else
		{
			for(int i=mn2; i<=mx2; i++)
			{
				if(ch[i].c==1) {puts("0"); return 0;}
			}
			int l = -1,r = -1;
			for(int i=mx2; ch[i].c!=1; i=(i==sz?1:i+1))
			{
				l++;
			}
			for(int i=mn2; ch[i].c!=1; i=(i==1?sz:i-1))
			{
				r++;
			}
			ans = 1ll*(l+1ll)*(r+1ll)%P;
		}
	}
	for(int i=1; i<=sz; i++)
	{
		f[ch[i].id] = true;
	}
	int cnt1 = 0,cnt2 = 0;
	for(int i=1; i<=n; i++)
	{
		if(f[i]==false && a[i].c==0) {ans=(ans<<1)%P;}
		if(a[i].c==1) cnt1++;
		if(a[i].c==2) cnt2++;
	}
	if(cnt1==0) {ans--;} if(cnt2==0) {ans--;}
	ans = (ans+P)%P;
	printf("%lld\n",ans);
	return 0;
}