np中的温故知新

1.一维数组中寻找与某个数最近的数

# 一维数组中寻找与某个数最近的数

Z=np.random.uniform(0,1,20)

print("随机数组：\n",Z)

z=0.5

m=Z.flat[np.abs(Z-z).argmin()]

m

随机数组：

 [0.87249114 0.64595395 0.10142435 0.46202885 0.15948433 0.53886897

 0.17802543 0.0885369  0.9859855  0.92086206 0.94694556 0.98142637

 0.98578709 0.58045542 0.96260882 0.42125302 0.06691017 0.60032047

 0.51668912 0.44761173]

Out[35]:

0.5166891167930422

2. 找出给定一维数组中非 0 元素的位置索引

Z = np.nonzero([1,0,2,0,1,0,4,0])

Z

(array([0, 2, 4, 6]),)

3.对于给定的 5x5 二维数组，在其内部随机放置 p 个值为 1 的数

p=3

Z=np.zeros((5,5))

z=np.copy(Z)

choice=np.random.choice(range(5*5), p, replace=False)

print(choice)

np.put(Z,choice,1)

print(Z)

np.put(z,np.random.choice(range(3*3),p,replace=False),1)

Z

[12 24  8]

[[0. 0. 0. 0. 0.]

 [0. 0. 0. 1. 0.]

 [0. 0. 1. 0. 0.]

 [0. 0. 0. 0. 0.]

 [0. 0. 0. 0. 1.]]

Out[103]:

array([[0., 0., 0., 0., 0.],

       [0., 0., 0., 1., 0.],

       [0., 0., 1., 0., 0.],

       [0., 0., 0., 0., 0.],

       [0., 0., 0., 0., 1.]])

4.对于随机的 3x3 二维数组，减去数组每一行的平均值

X=np.random.rand(3,3)

print(X)

print(X.mean(axis=1,keepdims=True))

print(X.mean(axis=1,keepdims=False))

Y=X-X.mean(axis=1,keepdims=True)

Y

[[0.85617766 0.21482728 0.44325087]

 [0.44365337 0.47689328 0.34798518]

 [0.96849106 0.99755228 0.05166133]]

[[0.50475194]

 [0.42284395]

 [0.67256822]]

[0.50475194 0.42284395 0.67256822]

Out[106]:

array([[ 0.35142572, -0.28992466, -0.06150107],

       [ 0.02080943,  0.05404934, -0.07485876],

       [ 0.29592283,  0.32498406, -0.62090689]])

5 获得二维数组点积结果的对角线数组

A=np.random.uniform(0,1,(3,3))

B=np.random.uniform(0,1,(3,3))

print(np.dot(A,B))

[[0.69147934 0.2526067  0.54456377]

 [1.88744045 1.39425446 1.01802782]

 [0.80716853 0.21709932 0.68321853]]

/慢方法
np.diag(np.dot(A,B))

[0.69147934 1.39425446 0.68321853]

/快方法
np.sum(A*B.T,axis=1)

[0.69147934 1.39425446 0.68321853]

# 更快的方法
np.einsum("ij, ji->i", A, B)

6.找到随机一维数组中前 p 个最大值

Z=np.random.randint(1,100,100)

print(Z)

p=5

# 法一

print(np.argsort(Z))

print(np.argsort(Z)[-p:])

z1=Z[np.argsort(Z)[-p:]]

print(z1)

# 法二

print(np.argsort(Z))

z2=Z[np.argsort(Z)]

print(z2)

print(z2[-p:])

[34 92 73 81 72 69 84 67 84 54 42 55 67 42 26 59 48 41 42 15 15 75 34 65

 56  4 82 85 33 10 51 69 32 59 51 76 13  2 48 55 22 25 44 11 28 62  8 31

 47 75 24 91 61 13 52 24 51 96 77 35 20 98 17 33 24 21 64 23 87 70 59 77

 46 37 90 67 46 24 81 59 29 31 74 67 68 23 43 12 21 37 94 24 69 32 89 20

 76 95 31 66]

[37 25 46 29 43 87 36 53 20 19 62 95 60 65 88 40 85 67 64 50 55 91 77 41

 14 44 80 47 81 98 32 93 28 63  0 22 59 73 89 17 10 18 13 86 42 72 76 48

 38 16 34 56 30 54  9 39 11 24 70 79 33 15 52 45 66 23 99 83  7 75 12 84

 92  5 31 69  4  2 82 21 49 96 35 58 71  3 78 26  6  8 27 68 94 74 51  1

 90 97 57 61]

[ 1 90 97 57 61]

[92 94 95 96 98]
---------------------------------------------------------------------------

[37 25 46 29 43 87 36 53 20 19 62 95 60 65 88 40 85 67 64 50 55 91 77 41

 14 44 80 47 81 98 32 93 28 63  0 22 59 73 89 17 10 18 13 86 42 72 76 48

 38 16 34 56 30 54  9 39 11 24 70 79 33 15 52 45 66 23 99 83  7 75 12 84

 92  5 31 69  4  2 82 21 49 96 35 58 71  3 78 26  6  8 27 68 94 74 51  1

 90 97 57 61]

[ 2  4  8 10 11 12 13 13 15 15 17 20 20 21 21 22 23 23 24 24 24 24 24 25

 26 28 29 31 31 31 32 32 33 33 34 34 35 37 37 41 42 42 42 43 44 46 46 47

 48 48 51 51 51 52 54 55 55 56 59 59 59 59 61 62 64 65 66 67 67 67 67 68

 69 69 69 70 72 73 74 75 75 76 76 77 77 81 81 82 84 84 85 87 89 90 91 92

 94 95 96 98]

[92 94 95 96 98]

7.对于二维随机数组中各元素，保留其 2 位小数

Z=np.random.random((5,5))

print(Z)

np.set_printoptions(precision=2)

Z

[[0.45389061 0.00459791 0.42885481 0.87764257 0.66726466]

 [0.79804312 0.54167802 0.67716846 0.3160879  0.2175134 ]

 [0.57729706 0.60136079 0.25779121 0.93762588 0.98816545]

 [0.11628811 0.46043354 0.2167248  0.63628797 0.84759436]

 [0.59625979 0.34086979 0.36992923 0.44203274 0.78498223]]

Out[161]:

array([[0.45, 0.  , 0.43, 0.88, 0.67],

       [0.8 , 0.54, 0.68, 0.32, 0.22],

       [0.58, 0.6 , 0.26, 0.94, 0.99],

       [0.12, 0.46, 0.22, 0.64, 0.85],

       [0.6 , 0.34, 0.37, 0.44, 0.78]])

4使用科学记数法输出 NumPy 数组

Z = np.random.random([5,5])

print(Z)

Z/1e3

[[0.01 0.9  0.64 0.68 0.46]

 [0.61 0.   0.4  0.09 0.02]

 [0.83 0.1  0.72 0.87 0.09]

 [0.49 0.15 0.37 0.43 0.27]

 [0.48 0.87 0.4  0.38 0.57]]

Out[88]:

array([[6.47e-06, 9.04e-04, 6.37e-04, 6.83e-04, 4.62e-04],

       [6.13e-04, 1.82e-06, 4.02e-04, 8.70e-05, 2.10e-05],

       [8.34e-04, 9.52e-05, 7.16e-04, 8.68e-04, 9.34e-05],

       [4.93e-04, 1.49e-04, 3.73e-04, 4.32e-04, 2.73e-04],

       [4.85e-04, 8.66e-04, 4.04e-04, 3.83e-04, 5.70e-04]])

5.使用 NumPy 找出百分位点（25%，50%，75%）

a=np.arange(15)

print(a)

np.percentile(a,q=[25,50,75])

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]

Out[165]:

array([ 3.5,  7. , 10.5])

6.找出数组中缺失值的总数及所在位置

# 生成含缺失值的 2 维数组

Z = np.random.rand(10,10)

Z[np.random.randint(10, size=5), np.random.randint(10, size=5)] = np.nan

Z

array([[0.8 , 0.25, 0.74, 0.05, 0.24, 0.16, 0.63, 0.62, 0.89, 0.85],

       [0.61, 0.76, 0.26, 0.3 , 0.82, 0.74, 0.96, 0.64, 0.58, 0.06],

       [0.78, 0.38, 0.19, 0.68, 0.75, 0.91, 0.13, 0.24, 0.98, 0.21],

       [0.47, 0.12, 0.34, 0.06, 0.46, 0.69, 0.1 ,  nan, 0.27, 0.92],

       [0.83, 0.01, 0.63, 0.15, 0.52, 0.52, 0.02, 0.  , 0.74, 0.59],

       [0.56, 0.66, 0.15,  nan, 0.26, 0.88, 0.15, 0.57, 0.61, 0.35],

       [0.33, 0.58, 0.06, 0.94, 0.58, 0.53, 0.97, 0.02, 0.32,  nan],

       [0.84, 0.71, 0.65, 0.42, 0.44, 0.96, 0.37, 0.65, 0.6 , 0.17],

       [0.04, 0.94, 0.92,  nan, 0.7 , 0.38, 0.28, 0.45, 0.35, 0.93],

       [0.38, 0.69, 0.43, 0.01, 0.67, 0.46, 0.73, 0.99, 0.94, 0.45]]

print("缺失值总数: \n", np.isnan(Z).sum())

print("缺失值索引: \n", np.where(np.isnan(Z)))

缺失值总数:

 4

缺失值索引:

 (array([3, 5, 6, 8]), array([7, 3, 9, 3]))
=>(3,7)(5,3)(6,9)(8,3)

#从随机数组中删除包含缺失值的行

Z[np.sum(np.isnan(Z),axis=1)==0]

6.统计随机数组中的各元素的数量

Z=np.random.randint(0,10,100).reshape(10,10)

print(Z)

np.unique(Z,return_counts=True)

[[0 0 0 8 1 6 2 8 4 4]

 [2 7 8 0 8 5 7 5 6 3]

 [7 0 0 9 3 4 7 5 7 3]

 [8 2 3 3 7 5 6 4 3 2]

 [4 9 9 1 0 4 0 4 7 8]

 [8 0 3 5 5 8 0 5 9 1]

 [4 9 9 1 2 0 7 0 9 0]

 [2 8 1 3 2 1 4 0 9 8]

 [9 9 7 6 7 1 3 5 6 9]

 [2 2 9 9 0 7 3 9 5 3]]

Out[22]:

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),

 array([15,  7,  9, 11,  9,  9,  5, 11, 10, 14]))

7.得到二维随机数组各行的最大值

Z = np.random.randint(1,100, [5,5])

print(Z)

np.amax(Z, axis=1)

[[92 27 63 19 73]

 [96 75 43 50 11]

 [ 5 32 62 92 13]

 [ 7  3 75 68 42]

 [63 27 94 82 88]]

Out[97]:

array([92, 96, 92, 75, 94])

Z=np.random.randint(1,100,[5,5])

print(Z)

np.apply_along_axis(np.min,arr=Z,axis=1)

[[82 92 48 60 13]

 [29 62 23 34 94]

 [55 59 18 62 45]

 [84 19 95 36 24]

 [54 90 44 31 42]]

Out[14]:

array([13, 23, 18, 19, 31])

8.计算两个数组之间的欧氏距离

a=np.array([1,2])

b=np.array([7,8])

print(np.sqrt(np.power((8-2),2)+np.power((7-1),2)))

　　8.48528137423857

9.求解给出矩阵的逆矩阵并验证

matrix = np.array([[1., 2.], [3., 4.]])

inverse_matrix = np.linalg.inv(matrix)

# 验证原矩阵和逆矩阵的点积是否为单位矩阵

assert np.allclose(np.dot(matrix, inverse_matrix), np.eye(2))

inverse_matrix

array([[-2. ,  1. ],

       [ 1.5, -0.5]])

10-12都是数据标准化处理
10.使用 Z-Score 标准化算法对数据进行标准化处理

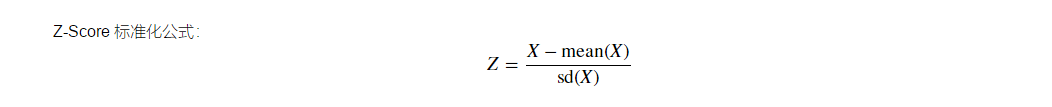
#根据Z-Scor公式定义函数

def zscore(x,axis=None):

    xmean=x.mean(axis=axis,keepdims=True)

    xstd=np.std(x,axis=axis,keepdims=True)

    zscore=(x-xmean)/xstd

    return zscore

#生成随机矩阵

Z=np.random.randint(10,size=(5,5))

print(Z)

zscore(Z)

[[9 7 1 9 6]

 [8 2 8 4 7]

 [2 6 7 1 5]

 [7 6 6 7 0]

 [7 9 5 5 3]]

Out[28]:

array([[ 1.35690061,  0.58593435, -1.72696441,  1.35690061,  0.20045123],

       [ 0.97141748, -1.34148129,  0.97141748, -0.57051503,  0.58593435],

       [-1.34148129,  0.20045123,  0.58593435, -1.72696441, -0.1850319 ],

       [ 0.58593435,  0.20045123,  0.20045123,  0.58593435, -2.11244754],

       [ 0.58593435,  1.35690061, -0.1850319 , -0.1850319 , -0.95599816]])

11.使用 Min-Max 标准化算法对数据进行标准化处理

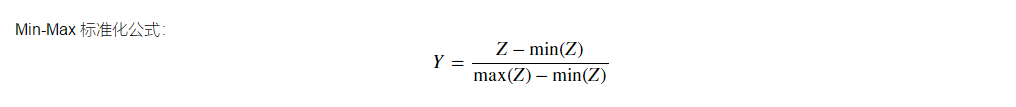
#数据公式熟悉

x=np.array([[1,2],[3,4]])

min=x.min(axis=None,keepdims=True)

mean=x.mean(axis=None,keepdims=True)

print(min)

print(mean)

print(x-min)

[[1]]

[[2.5]]

[[0 1]

 [2 3]]
#定义Min-Max 标准化公式

def min_max(x,axis=None):

    min=x.min(axis=axis,keepdims=True)

    max=x.max(axis=axis,keepdims=True)

    result=(x-min)/(max-min)

    return result

#生成随机数据

Z=np.random.randint(10,size=(5,5))

print(Z)

print(Z.min())

#

print(Z.max())

#
min_max(Z)

[[4 6 8 0 3]

 [9 2 6 3 0]

 [3 0 6 5 9]

 [1 5 2 6 8]

 [4 0 4 3 7]]

0

9

Out[37]:

array([[0.44444444, 0.66666667, 0.88888889, 0.        , 0.33333333],

       [1.        , 0.22222222, 0.66666667, 0.33333333, 0.        ],

       [0.33333333, 0.        , 0.66666667, 0.55555556, 1.        ],

       [0.11111111, 0.55555556, 0.22222222, 0.66666667, 0.88888889],

       [0.44444444, 0.        , 0.44444444, 0.33333333, 0.77777778]])

12.使用 L2 范数对数据进行标准化处理

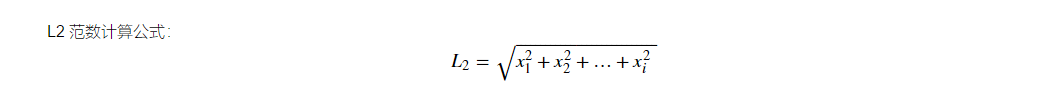
x=np.array([[1,1],
[2,2]])

#axis=1 按列算行
l2 = np.linalg.norm(x, ord = 2, axis=1, keepdims=True)
print(l2)
#非零处理
l2[l2==0]=1
print(l2)

array([[1.41421356],

       [2.82842712]])

array([[1.41421356],

       [2.82842712]])

# 根据l2公式定义函数

def l2_normalize(v, axis=-1, order=2):

    l2 = np.linalg.norm(v, ord = order, axis=axis, keepdims=True)

    l2[l2==0] = 1

    return v/l2

# 生成随机数据

Z = np.random.randint(10, size=(5,5))

print(Z)

l2_normalize(Z)

[[5 6 6 9 7]

 [1 8 5 1 8]

 [6 1 3 5 3]

 [7 1 2 6 0]

 [9 4 0 8 8]]

Out[104]:

array([[0.33, 0.4 , 0.4 , 0.6 , 0.46],

       [0.08, 0.64, 0.4 , 0.08, 0.64],

       [0.67, 0.11, 0.34, 0.56, 0.34],

       [0.74, 0.11, 0.21, 0.63, 0.  ],

       [0.6 , 0.27, 0.  , 0.53, 0.53]])

13 keepdims 属性的含义

import numpy as np

a = np.array([[1,2],[3,4]])

# 按行相加，并且保持其二维特性

print(np.sum(a, axis=1, keepdims=True))

# 按行相加，不保持其二维特性

print(np.sum(a, axis=1))

输出

[[3]

 [7]]
-------

[3 7]


14.计算变量直接的相关性系数

Z = np.array([

    [1, 2, 1, 9, 10, 3, 2, 6, 7], # 特征 A

    [2, 1, 8, 3, 7, 5, 10, 7, 2], # 特征 B

    [2, 1, 1, 8, 9, 4, 3, 5, 7]]) # 特征 C

np.corrcoef(Z)

　　　　 [A]     [B]     [C]

array([[ 1.  , -0.06,  0.97]   [A]

       [-0.06,  1.  , -0.01],  [B]

       [ 0.97, -0.01,  1.  ]]) [C]

相关性系数取值从 0-1 变换，靠近 1 则代表相关性较强。结果如下所示，变量 A 与变量 A 直接的相关性系数为 1，因为是同一个变量；变量 A 与变量 B 之间的相关性系数为 -0.06，说明几乎不相关。变量 A 与变量 C 之间的相关性系数为 0.97，说明相关性较强

15.计算矩阵的特征值和特征向量

M = np.matrix([[1,2,3], [4,5,6], [7,8,9]])

w, v = np.linalg.eig(M)

# w 对应特征值，v 对应特征向量

w, v

(array([ 1.61168440e+01, -1.11684397e+00, -9.75918483e-16]),

 matrix([[-0.23197069, -0.78583024,  0.40824829],

         [-0.52532209, -0.08675134, -0.81649658],

         [-0.8186735 ,  0.61232756,  0.40824829]]))

可以通过 P'AP=M 公式反算，验证是否能得到原矩阵。

v*np.diag(w)*np.linalg.inv(v)

matrix([[1., 2., 3.],

        [4., 5., 6.],

        [7., 8., 9.]])

16.数组连接
　　　按行连接两个数组

M1 = np.array([1, 2, 3])

M2 = np.array([4, 5, 6])

np.r_[M1, M2]

array([1, 2, 3, 4, 5, 6])
　　
　　按列连接两个数组

M1 = np.array([1, 2, 3])

M2 = np.array([4, 5, 6])

np.c_[M1, M2]

array([[1, 4],

       [2, 5],

       [3, 6]])
　　
　　将多个 1 维数组拼合为单个 Ndarray:

Z1=np.arange(3)

Z2=np.arange(3,7)

Z3=np.arange(7,10)

Z=np.array([Z1,Z2,Z3])

print(Z)

np.concatenate(Z)

[array([0, 1, 2]) array([3, 4, 5, 6]) array([7, 8, 9])]

Out[8]:

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np中的温故知新的更多相关文章

np中的随机函数
numpy.random.uniform介绍: 1. 函数原型: numpy.random.uniform(low,high,size) ==>也即其他函数是对该函数的进一步封装功能: ...
转载什么是P问题、NP问题和NPC问题
原文地址http://www.matrix67.com/blog/archives/105 这或许是众多OIer最大的误区之一. 你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这个只有搜 ...
浅谈P NP NPC
P问题:多项式时间内可以找到解的问题,这个解可以在多项式时间内验证. NP问题:有多项式时间内可以验证的解的问题,而并不能保证可以在多项式时间内找到这个解. 比如汉密尔顿回路,如果找到,在多项式时间内 ...
P和NP问题
1. 通俗详细地讲解什么是P和NP问题 http://blog.sciencenet.cn/blog-327757-531546.html NP----非定常多项式(英语:non-determin ...
P问题、NP问题、NPC问题、NP难问题的概念
P问题.NP问题.NPC问题.NP难问题的概念离入职尚有几天时间,闲来无事,将大家常见却又很容易搞糊涂的几个概念进行整理,希望对大家有所帮助.你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这 ...
P问题、NP问题和NPC问题
P问题.NP问题和NPC问题这或许是众多OIer最大的误区之一. 你会经常看到网上出现“这怎么做,这不是NP问题吗”.“这个只有搜了,这已经被证明是NP问题了”之类的话.你要知道,大多数人此时 ...
P==NP？？
注:基础知识见下方下面是关于P==NP ??? 一些讨论,挺好玩的. 1. 首先强调一下数学上还没有证明这个问题!但是我们看看其他角度来看这个问题. 其次,心理上来说,要是可以证明P==NP那么早 ...
（转）什么是P问题、NP问题和NPC问题
这或许是众多OIer最大的误区之一. 你会经常看到网上出现"这怎么做,这不是NP问题吗"."这个只有搜了,这已经被证明是NP问题了"之类的话.你要知道,大 ...
NP完整性| 集1（简介）
我们一直在写关于高效算法来解决复杂问题,如最短路径,欧拉图,最小生成树等.这些都是算法设计者的成功故事. 在这篇文章中,讨论了计算机科学的失败故事. 计算机可以解决所有的计算问题吗? 存在计算问题,即 ...

随机推荐

剑指offer49：把字符串转换成整数
1 题目描述将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能,但是string不符合数字要求时返回0),要求不能使用字符串转换整数的库函数. 数值为0或者字符串不 ...
Python基础第三章使用字符串（1）精简版
所有标准序列操作(索引,切片,乘法,成员资格检查,长度,最小值,最大值)都适于字符串. 但,字符串是不可变得,故所有得元素赋值和切片赋值都是非法的. 1. %s 转换说明符设置字符串格式 %左边指定 ...
Python利用PIL将数值矩阵转化为图像
要求:输入一个n*n的矩阵,矩阵包括从-1到1的浮点数,将其转化为可视化图像调库 from PIL import Image import numpy as np import math 载入图像, ...
C++反汇编第三讲,反汇编中识别继承关系,父类,子类,成员对象
讲解目录: 1.各类在内存中的表现形式备注: 主要复习开发知识,和反汇编没有关系,但是是理解反汇编的前提. 2.子类继承父类 2.1 子类中有虚函数,父类中有虚函数 : 都有的情况下 ...
[Vue]method与计算属性computed、侦听器watch与计算属性computed的区别
一.方法method与计算属性computed的区别方法method:每当触发重新渲染时,调用方法method将总会再次执行函数: 计算属性computed:计算属性computed是基于它们的响应 ...
Windows 编程键盘
键盘对于大家来说可能再也熟悉不过了,它和鼠标是现在最常用的电脑输入设备.虽然在现在的图形界面操作系统下使用鼠标比使用键盘更方便.更广泛,但是鼠标还是一时半会儿取代不了它的老前辈——键盘的地位,尤其是在 ...
mysql 8.0.13开启远程连接配置方式
1:linux登录mysql [root@localhost mysql]# mysql -u root -p Enter password: Welcome to the MySQL monitor ...
路由组件传参-props解耦方式（主要）
在组件中使用 $route 会使之与其对应路由形成高度耦合,从而使组件只能在某些特定的 URL 上使用,限制了其灵活性. 使用 props 将组件和路由解耦: 取代与 $route 的耦合 const ...
Boost,Eigen,Flann—C++标准库预备役
Boost,Eigen,Flann—C++标准库预备役第一预备役:Boost Boost库是为C++语言标准库提供扩展的一些C++程序库的总称. Boost库由Boost社区组织开发.维护 ...
QT Creator 使用SVN的版本号做为编译的版本信息
在使用qt Creator 开发中,如果想使用 svn 的源代码版本号来作为 build 的一个子版本号或者只是为了识别某个发布版本,与源代码的版本信息对应起来,可以方便调试对应的版本代码,我们可以通 ...

np中的温故知新

np中的温故知新的更多相关文章

随机推荐

热门专题