拓扑排序（Toposort）

摘自：https://blog.csdn.net/qq_35644234/article/details/60578189

《图论算法》

1、拓扑排序的介绍

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。
拓扑排序对应施工的流程图具有特别重要的作用，它可以决定哪些子工程必须要先执行，哪些子工程要在某些工程执行后才可以执行。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系，可用一个有向图来表示，图中的顶点代表活动(子工程)，图中的有向边代表活动的先后关系，即有向边的起点的活动是终点活动的前序活动，只有当起点活动完成之后，其终点活动才能进行。

通常，我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network)，简称AOV网。

在AOV网络中，如果存在有向边<u,v>则活动u必须在活动v之前进行，则称u是v的直接前驱(Immediate Predecessor)，v是u的直接后继（Immediate Successor）。如果存在<u,u1,u2,u3,u4,u5...un,v>则称u是v的前驱，v是u的后继。

这种前驱和后继具有传递性，例如v2是v1的前驱，v3是v2的前驱，同样v3也是v1的前驱。另外这种活动不能将自己作为自己的前驱或者后继，这种特性是反自反性质。

一个AOV网应该是一个有向无环图，即不应该带有回路，因为若带有回路，则回路上的所有活动都无法进行（对于数据流来说就是死循环）。在AOV网中，若不存在回路，则所有活动可排列成一个线性序列，使得每个活动的所有前驱活动都排在该活动的前面，我们把此序列叫做拓扑序列(Topological order)，由AOV网构造拓扑序列的过程叫做拓扑排序(Topological sort)。AOV网的拓扑序列不是唯一的，满足上述定义的任一线性序列都称作它的拓扑序列。

2、拓扑排序的实现步骤

在有向图中选一个没有前驱的顶点并且输出
    从图中删除该顶点和所有以它为尾的弧（白话就是：删除所有和它有关的边）
    重复上述两步，直至所有顶点输出，或者当前图中不存在无前驱的顶点为止，后者代表我们的有向图是有环的，因此，也可以通过拓扑排序来判断一个图是否有环。

3、拓扑排序示例手动实现

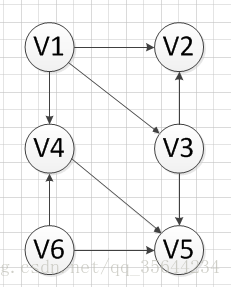
如果我们有如下的一个有向无环图，我们需要对这个图的顶点进行拓扑排序，过程如下：

首先，我们发现V6和v1是没有前驱的，所以我们就随机选去一个输出，我们先输出V6，删除和V6有关的边，得到如下图结果：

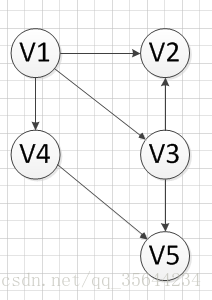
然后，我们继续寻找没有前驱的顶点，发现V1没有前驱，所以输出V1，删除和V1有关的边，得到下图的结果： 

然后，我们又发现V4和V3都是没有前驱的，那么我们就随机选取一个顶点输出（具体看你实现的算法和图存储结构），我们输出V4，得到如下图结果： 

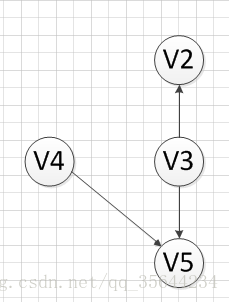
然后，我们输出没有前驱的顶点V3，得到如下结果： 

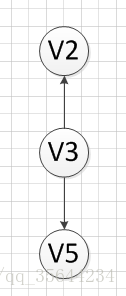
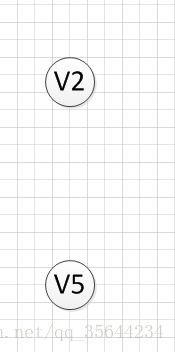
然后，我们分别输出V5和V2，最后全部顶点输出完成，该图的一个拓扑序列为：

v6–>v1—->v4—>v3—>v5—>v2

通过邻接矩阵来实现的代码：

 #include<cstdio>
 #include<cstring>
 int ans[][];///邻接矩阵，记录二者是否有关联
 int n,indegree[];///记录节点个数
 int queue[];///保存拓扑
 void topsort()
 {
     int i,j,top,k=;
     for(j=; j<n; ++j)///遍历n次
     {
         for(i=; i<=n; ++i)
         {
             if(indegree[i]==)///找到入度为0的节点
             {
                 top=i;
                 break;
             }
         }
         queue[k++]=top;///当前第一名入队列，也可以直接输出
         indegree[top]=-;///该节点的入度更新为-1，避免重复入队列
         for(i=; i<=n; ++i)
         {
             if(ans[top][i])///删除与该店关联的边
                 indegree[i]--;
         }
     }
     for(i=; i<k-; ++i)
         printf("%d ",queue[i]);
     printf("%d\n",queue[n-]);
 }

 int main()
 {
     int i,a,b,m;
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         memset(indegree,,sizeof(indegree));///数组初始化为0
         memset(ans,,sizeof(ans));///数组初始化为0
         for(i=; i<m; ++i)
         {
             scanf("%d%d",&a,&b);
             if(ans[a][b]==)
             {
                 ans[a][b]=;///二者有关联
                 indegree[b]++;///记录前驱数量
             }
         }
         topsort();
     }
     return ;
 }