Comet OJ - Contest #2简要题解
Comet OJ - Contest #2简要题解
前言:
我没有小裙子,我太菜了。
A 因自过去而至的残响起舞
https://www.cometoj.com/contest/37/problem/A?problem_id=1528
- 容易发现那玩意增长的飞快,只要模拟就可以了
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
ll n;
ll f[100000];
int main() {
int i;
scanf("%lld",&n);
f[1]=1,f[2]=1;
ll sum=2;
if(n==1) {puts("2"); return 0;}
//if(n==2) {puts("2"); return 0;}
for(i=3;i<=10000;i++) {
f[i]=sum/2;
sum+=f[i];
if(sum>n) {
printf("%d\n",i); return 0;
}
}
}
B 她的想法、他的战斗
https://www.cometoj.com/contest/37/problem/B?problem_id=1529
- 根据期望的线性性,可知\(E(q)=\frac{L+R}{2}\), 那么利润就是\(\frac{p-l}{r-l}(E(q)-p)\)
- 不难发现这东西是个二次函数,直接求最大值就可以了。
- 最优的\(p\)不在\([l,r]\)区间时需要特判。
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
typedef double f2;
ll n;
ll f[100000];
int main() {
f2 l,r,L,R;
scanf("%lf%lf%lf%lf",&l,&r,&L,&R);
f2 q=(L+R)*0.5;
f2 x=(q+l)/2;
if(x<l) {
puts("0.0000"); return 0;
}
f2 ans;
if(x>r) {
ans=q-r;
}
else ans=(-x*x+(q+l)*x-l*q)/(r-l);
if(ans<1e-6) ans=0;
printf("%.4f\n",ans);
}
C 言论的阴影里妄想初萌
https://www.cometoj.com/contest/37/problem/C?problem_id=1530
- 枚举有多少个点即可。
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
using namespace std;
typedef long long ll;
typedef double f2;
#define N 100050
#define mod 998244353
int n;
ll P,fac[N],inv[N];
ll qp(ll x,ll y=mod-2) {
ll re=1; for(;y;y>>=1,x=x*x%mod) if(y&1) re=re*x%mod; return re;
}
ll C(int x,int y) {
return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
int main() {
int i;
ll x,y;
scanf("%d%lld%lld",&n,&x,&y);
P=x*qp(y)%mod;
for(fac[0]=i=1;i<=n;i++) fac[i]=fac[i-1]*i%mod;
inv[n]=qp(fac[n]);
for(i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
ll ans=0;
for(i=0;i<=n;i++) {
ans=(ans+C(n,i)*qp(P,ll(i)*(i-1)/2))%mod;
}
printf("%lld\n",ans);
}
D 错综的光影所迷惑的思念是
https://www.cometoj.com/contest/37/problem/D?problem_id=1531
- 不难想到先枚举点集直径的中点\(x\),那么限制就是距离\(x\)为\(\frac{i}{2}\)的点在不同的子树中至少要选出两个,其他小于\(i\)的可以随意选。
- 是一个类似\(2^{sz(x)}-1-\sum\limits_{t}(2^{sz(t)}-1)\)的一个式子。其中\(sz(t)\)表示以\(x\)为根,\(t\)的子树内有多少距离\(x\)为\(i\)的点。
- 有两个问题,一是点集直径中点可能卡在边上,二是\(i\)可能是奇数,我们在每条边上塞一个点就行了。
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 4050
int n,head[N],to[N<<1],nxt[N<<1],cnt;
ll mi[N],ans[N];
int siz[N],ssiz[N][N];
inline void add(int u,int v) {
to[++cnt]=v; nxt[cnt]=head[u]; head[u]=cnt;
}
void dfs(int x,int y,int d,int t) {
int i;
if(x<=n) {
siz[d]++; ssiz[t][d]++;
}
for(i=head[x];i;i=nxt[i]) if(to[i]!=y) {
dfs(to[i],x,d+1,t);
}
}
int main() {
scanf("%d",&n);
int i,x,y,j;
for(i=1;i<n;i++) scanf("%d%d",&x,&y),add(x,n+i),add(n+i,x),add(y,n+i),add(n+i,y);
int ln=n+n-1;
for(mi[0]=i=1;i<=ln;i++) mi[i]=(mi[i-1]<<1)%mod;
for(x=1;x<=ln;x++) {
int s=0,lst=0;
memset(siz,0,sizeof(siz));
if(x<=n) {
siz[0]++; lst++;
}
for(i=head[x];i;i=nxt[i]) {
s++;
memset(ssiz[s],0,sizeof(ssiz[s]));
dfs(to[i],x,1,s);
}
for(i=1;i<n;i++) {
ll tmp=mi[siz[i]]-1;
for(j=1;j<=s;j++) tmp=(tmp-(mi[ssiz[j][i]]-1))%mod;
ans[i]=(ans[i]+tmp*mi[lst])%mod;
lst+=siz[i];
}
}
for(i=1;i<n;i++) printf("%lld\n",(ans[i]+mod)%mod);
}
E 情报强者追逐事件
https://www.cometoj.com/contest/37/problem/E?problem_id=1532
- 对于不在环上的那些,转移是可以直接合并的,按照拓扑序更新即可,转移类似\(f_x=f_x+(1-f_x)\times f_y\times s_y\)。
- 剩下的对于每个环来考虑,对于\(x\),会被环上的任意一点\(y\)来更新到,如果在某一时刻环上相邻两个点\(u\)和\(v\),且从\(u\)转移出来的概率是\(p\),那么从\(v\)转移出去的概率就是\((1-f_v)\times s_u\times p+f_v\),不难发现这是一个\(ax+b\)的形式,放到线段树上去维护就好了。
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 800050
char buf[100000],*p1,*p2;
int to[N],du[N],Q[N],n;
ll P[N],s[N],f[N];
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int rd() {
int x=0; char s=nc();
while(s<'0'||s>'9') s=nc();
while(s>='0'&&s<='9') x=(((x<<2)+x)<<1)+s-'0',s=nc();
return x;
}
ll qp(ll x,ll y=mod-2) {
ll re=1;for(;y;y>>=1,x=x*x%mod)if(y&1)re=re*x%mod; return re;
}
struct A {
ll x,y;
A() {x=y=0;}
A(ll x_,ll y_) {x=x_,y=y_;}
A operator + (const A &u) const {
return A(x*u.x%mod, (y*u.x+u.y)%mod);
}
}tr[N<<2];
#define ls p<<1
#define rs p<<1|1
int S[N],tp;
void build(int l,int r,int p) {
if(l==r) {
int x=l%tp;
if(!x)x=tp;
x=S[x];
int y=(l-1)%tp;
if(!y)y=tp;
y=S[y];
tr[p]=A((1-f[x])*s[y]%mod,f[x]);
return ;
}
int mid=(l+r)>>1;
build(l,mid,ls); build(mid+1,r,rs);
tr[p]=tr[ls]+tr[rs];
}
A query(int l,int r,int x,int y,int p) {
if(x<=l&&y>=r) return tr[p];
int mid=(l+r)>>1;
if(y<=mid) return query(l,mid,x,y,ls);
else if(x>mid) return query(mid+1,r,x,y,rs);
else return query(l,mid,x,y,ls)+query(mid+1,r,x,y,rs);
}
void dfs(int x) {
if(!x||!du[x]) return ;
S[++tp]=x;
du[x]=0;
dfs(to[x]);
}
int main() {
n=rd();
int i;
ll x,y;
for(i=1;i<=n;i++) {
x=rd(),y=rd();
P[i]=x*qp(y)%mod;
}
for(i=1;i<=n;i++) to[i]=rd();
for(i=1;i<=n;i++) du[to[i]]++;
for(i=1;i<=n;i++) f[i]=P[i];
for(i=1;i<=n;i++) {
x=rd(),y=rd();
s[i]=x*qp(y)%mod;
}
int l=0,r=0;
for(i=1;i<=n;i++) if(!du[i]) {
Q[r++]=i;
}
while(l<r) {
int x=Q[l++];
du[to[x]]--;
f[to[x]] = (f[to[x]]+(1-f[to[x]])*f[x]%mod*s[x])%mod;
if(!du[to[x]]) {
Q[r++]=to[x];
}
}
//printf("%d\n",r);
//for(i=0;i<n;i++) printf("%d\n",Q[i]);
int j;
for(i=1;i<=n;i++) {
if(du[i]) {
//puts("FUCK");
tp=0;
dfs(i);
//puts("FUCK");
build(1,tp<<1,1);
//puts("FUCK");
for(j=1;j<=tp;j++) f[S[j]]=query(1,tp<<1,j+1,tp+j,1).y;
//printf("%d\n",tp);
}
f[i]=(f[i]%mod+mod)%mod;
printf("%lld",f[i]);
if(i!=n) printf(" ");
}
}
F 真实无妄她们的人生之路
比赛时:
woc这个F我会啊,赶紧写赶紧写
woc我怎么写了两个小时还没过啊
woc终于过了,但是我没小裙子了...
https://www.cometoj.com/contest/37/problem/E?problem_id=1532
- 设\(w_i=\frac{P_i}{1-P_i}\),表示选\(i\)产生的概率,最后答案再乘上\(\prod\limits_{i}(1-P_i)\)就可以了。
- 设\(f_j=[x^j](\prod\limits_{i=1}^{n}(w_ix+1))\),也就是选\(j\)个的概率,这个可以分治\(ntt\)求出。
- 那么考虑删掉一个,假设删掉第\(i\)个,设退掉\(i\)之后的背包数组为\(g_j\)就是强制\(i\)不选,选\(j\)个的概率。
- 根据退背包那一套理论,可以得出\(g_j=f_j-g_{j-1}\times w_i\)
- 展开,可得\(g_j=\sum\limits_{k=0}^j(-1)^kw_i^kf_{j-k}\)
- 那么退掉第\(i\)个的答案\(ans_i=\sum\limits_{j=1}^na_j\sum\limits_{k=0}^j(-1)^kw_i^kf_{j-k}\)
- \(ans_i=\sum\limits_{k=0}^n(-1)^kw_i^k\sum\limits_{j=k}^na_jf_{j-k}\)
- 设\(h_k=\sum\limits_{j=k}^na_jf_{j-k}\),这是一个卷积形式。
- 那么\(ans_i=\sum\limits_{k=0}^n(-1)^kw_i^kh_k\), 多点求值即可。
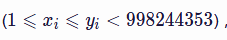
- 把概率为\(1\)的扔掉再把\(a\)数组平移若干位来求其他位置上的答案然后由于那些被扔掉的位置答案都相同所以用一开始的\(f\)和平移(若干位\(-1\))后的\(a\)数组求点积即可。
- 或者把上面的\(w_i\)改成\(\frac{1-P_i}{P_i}\),orzzsy。
//❤ ayaponzu*
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#include <queue>
using namespace std;
typedef long long ll;
#define mod 998244353
#define N 800050
char buf[100000],*p1,*p2;
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int rd() {
int x=0; char s=nc();
while(s<'0'||s>'9') s=nc();
while(s>='0'&&s<='9') x=(((x<<2)+x)<<1)+s-'0',s=nc();
return x;
}
ll mem[N*60],*ptr=mem,fac[N],inv[N];
ll qp(ll x,ll y) {ll re=1;for(;y;y>>=1,x=x*x%mod)if(y&1)re=re*x%mod;return re;}
ll INV(ll x){return qp(x,mod-2);}
void ntt(ll *a,int len,int flg) {
int i,j,k,t; ll tmp,w,wn;
for(i=k=0;i<len;i++) {
if(i>k) swap(a[i],a[k]);
for(j=len>>1;(k^=j)<j;j>>=1) ;
}
for(k=2;k<=len;k<<=1) {
t=k>>1; wn=qp(3,(mod-1)/k);
if(flg==-1) wn=INV(wn);
for(i=0;i<len;i+=k) {
w=1;
for(j=i;j<i+t;j++) {
tmp=a[j+t]*w%mod;
a[j+t]=(a[j]-tmp)%mod;
a[j]=(a[j]+tmp)%mod;
w=w*wn%mod;
}
}
}if(flg==-1)for(tmp=INV(len),i=0;i<len;i++) a[i]=a[i]*tmp%mod;
}
ll A[N],B[N];
struct shion {
ll *a;
int len;
shion() {}
shion(int l) {len=l,a=ptr,ptr+=l;}
void fix(int l) {len=l,a=ptr,ptr+=l;}
void rev() {reverse(a,a+len);}
void get_mod(int l) {int i;for(i=l;i<len;i++)a[i]=0;len=l;}
void kuo(int l) {len=l,ptr=mem+len;}
bool operator < (const shion &u) const {
return len>u.len;
}
shion operator - (const shion &u) const {
shion re(len);int i;
for(i=0;i<len;i++) re.a[i]=(a[i]-u.a[i])%mod;
return re;
}
shion operator + (const shion &u) const {
shion re(max(len,u.len)); int i;
for(i=0;i<re.len;i++) {
re.a[i]=((i<len?a[i]:0)+(i<u.len?u.a[i]:0))%mod;
}return re;
}
shion operator * (const shion &u) const {
shion re(len+u.len-1);
int i,l=1,j;
if(re.len<=200) {
for(i=0;i<len;i++)for(j=0;j<u.len;j++) {
re.a[i+j]=(re.a[i+j]+ll(a[i])*u.a[j])%mod;
}return re;
}
while(l<len+u.len)l<<=1;
memset(A,0,sizeof(ll)*l);
memset(B,0,sizeof(ll)*l);
memcpy(A,a,sizeof(ll)*len);
memcpy(B,u.a,sizeof(ll)*u.len);
ntt(A,l,1),ntt(B,l,1);
for(i=0;i<l;i++) A[i]=ll(A[i])*B[i]%mod;
ntt(A,l,-1);
for(i=0;i<re.len;i++) re.a[i]=A[i];
return re;
}
void get_inv(const shion &u,int len) {
if(len==1) {a[0]=INV(u.a[0]);return ;}
get_inv(u,len>>1);
int l=len<<1,i;
memset(A,0,sizeof(ll)*l);
memset(B,0,sizeof(ll)*l);
memcpy(A,u.a,sizeof(ll)*min(u.len,len));
memcpy(B,a,sizeof(ll)*len);
ntt(A,l,1),ntt(B,l,1);
for(i=0;i<l;i++) A[i]=B[i]*(2-ll(A[i])*B[i]%mod)%mod;
ntt(A,l,-1);
memcpy(a,A,sizeof(ll)*len);
}
shion Get_inv(int l) {
shion re(l); re.get_inv(*this,l); return re;
}
shion operator / (shion u) {
int n=len,m=u.len,l=1;
while(l<(n-m+1))l<<=1;
rev(),u.rev();
shion v=u.Get_inv(l);
v.get_mod(n-m+1);
shion re=*this*v;
rev(),u.rev();
re.get_mod(n-m+1);
re.rev();
return re;
}
shion operator % (shion u) {
shion re=*this-u*(*this/u); re.get_mod(u.len-1); return re;
}
shion Get_dao() {
shion re(len-1);
int i;
for(i=1;i<len;i++) re.a[i-1]=ll(i)*a[i]%mod;
return re;
}
}fq[N<<2];
#define ls p<<1
#define rs p<<1|1
ll RE[N],qx[N];
void build(int l,int r,int p) {
if(l==r) {
fq[p].fix(2);
fq[p].a[0]=-qx[l];
fq[p].a[1]=1;
return ;
}
int mid=(l+r)>>1;
build(l,mid,ls),build(mid+1,r,rs);
fq[p]=fq[ls]*fq[rs];
}
void get_val(shion F,int l,int r,int p,ll *re) {
if(F.len<=450) {
int i,j;
ll t;
for(i=l;i<=r;i++) {
for(j=0,t=1;j<F.len;j++,t=ll(t)*qx[i]%mod) {
re[i]=(re[i]+ll(t)*F.a[j])%mod;
}
}
return ;
}
int mid=(l+r)>>1;
get_val(F%fq[ls],l,mid,ls,re);
get_val(F%fq[rs],mid+1,r,rs,re);
}
priority_queue<shion>q;
int n;
ll P[N],a[N],f[N],g[N],num[N],h[N],tmpa[N];
void geth() {
shion ta(n+1),tb(n+1);
int i;
for(i=0;i<=n;i++) ta.a[i]=a[n-i];
for(i=0;i<=n;i++) tb.a[i]=f[i];
shion tc=ta*tb;
for(i=0;i<=n;i++) h[i]=tc.a[n-i];
}
int is[N],to[N];
int main() {
n=rd();
int i,tot=0,ln=n;
ll x,y;
for(i=0;i<n;i++) a[i]=rd();
for(i=1;i<=ln;i++) {
x=rd(),y=rd();
P[i]=x*INV(y)%mod;
num[i]=INV(1-P[i]);
if(P[i]==1) {
is[i]=1;
}else {
P[++tot]=P[i];
num[tot]=num[i];
to[i]=tot;
}
}
if(!tot) {
for(i=1;i<=n;i++) {
printf("%lld",a[ln-1]);
if(i!=n) printf(" ");
}
return 0;
}
memcpy(tmpa,a,sizeof(a));
for(i=0;i<=n;i++) a[i]=a[i+ln-tot];
n=tot;
for(i=1;i<=n;i++) {
shion t(2);
t.a[0]=1,t.a[1]=P[i]*num[i]%mod;
q.push(t);
}
for(i=1;i<n;i++) {
shion aa=q.top(); q.pop();
shion bb=q.top(); q.pop();
q.push(aa*bb);
}
ll tmp=1;
for(i=1;i<=n;i++) tmp=tmp*(1-P[i])%mod;
shion qwq=q.top();
for(i=0;i<=n;i++) f[i]=qwq.a[i];
geth();
for(i=1;i<=n;i++) qx[i]=P[i]*num[i]%mod;
build(1,n,1);
shion ff(n+1);
for(i=0;i<=n;i++) {
if(i&1) ff.a[i]=mod-h[i];
else ff.a[i]=h[i];
}
get_val(ff,1,n,1,RE);
if(tot!=ln) for(i=0;i<=n;i++) a[i]=tmpa[i+ln-tot-1];
ll OTH=0;
for(i=0;i<=n;i++) {
//printf("%lld\n",a[i]);
OTH=(OTH+a[i]*f[i])%mod;
}
OTH=(OTH*tmp%mod+mod)%mod;
for(i=1;i<=ln;i++) {
if(is[i]) {
printf("%lld",OTH);
}else {
ll ans=RE[to[i]]*num[to[i]]%mod*tmp%mod;
printf("%lld",(ans+mod)%mod);
}
if(i!=ln) printf(" ");
}
}

Comet OJ - Contest #2简要题解的更多相关文章
- Comet OJ - Contest #2 简要题解
Comet OJ - Contest #2 简要题解 cometoj A 模拟,复杂度是对数级的. code B 易知\(p\in[l,r]\),且最终的利润关于\(p\)的表达式为\(\frac{( ...
- Comet OJ - Contest #5 简要题解
好久没更博了,还是象征性地更一次. 依然延续了简要题解的风格. 题目链接 https://cometoj.com/contest/46 题解 A. 迫真字符串 记 \(s_i\) 表示数字 \(i\) ...
- Comet OJ Contest #13 简要题解
C2 首先用并查集维护\(1\)的连通块,然后用另外一个并查集维护第\(i\)行中,第\(j\)列之后的第一个\(0\)的位置,就是如果当前位置是\(1\)那么它的父亲是它右边的格子,否则是它自己. ...
- 【题解】Comet OJ Round 70 简要题解
[题解]Comet OJ Round 70 简要题解 A 将放在地上的书按照从小到大排序后,问题的本质就变成了合并两个序列使得字典序最小.可以直接模拟归并排序.直接用循环和std::merge实现这个 ...
- Comet OJ - Contest #11 题解&赛后总结
Solution of Comet OJ - Contest #11 A.eon -Problem designed by Starria- 在模 10 意义下,答案变为最大数的最低位(即原数数位的最 ...
- Comet OJ - Contest #5
Comet OJ - Contest #5 总有一天,我会拿掉给\(dyj\)的小裙子的. A 显然 \(ans = min(cnt_1/3,cnt_4/2,cnt5)\) B 我们可以感性理解一下, ...
- Comet OJ - Contest #4--前缀和
原题:Comet OJ - Contest #4-B https://www.cometoj.com/contest/39/problem/B?problem_id=1577传送门 一开始就想着暴力打 ...
- Comet OJ - Contest #8
Comet OJ - Contest #8 传送门 A.杀手皇后 签到. Code #include <bits/stdc++.h> using namespace std; typede ...
- Comet OJ - Contest #13-C2
Comet OJ - Contest #13-C2 C2-佛御石之钵 -不碎的意志-」(困难版) 又是一道并查集.最近做过的并查集的题貌似蛮多的. 思路 首先考虑,每次处理矩形只考虑从0变成1的点.这 ...
随机推荐
- 如何配置Smarty模板
<?php //首先包含Smarty类文件 include_once('Smarty/Smarty.class.php'); //实例化Smarty类文件 $smarty=new Smarty( ...
- linux机器之间拷贝和同步文件命令
1 不同机器拷贝文件 scp 文件 登录用户@机器IP:/目录/子目录 scp filename test@10.20.130.202:/home/test/ 2 文件[夹]同步 rsync ...
- 合并两个dt
C#代码中实现两个表(DataTable)的关联查询(JOIN) 之前通常都是使用SQL直接从数据库中取出表1和表2关联查询后的数据,只需要用一个JOIN就可以了,非常方便.近日遇到一种情况,两个 ...
- wpf窗口阴影
https://www.cnblogs.com/yiyan127/p/6362509.html
- 在 Confluence 6 中的 Jira 权限
只读(Read Only) 从你 JIRA 应用服务器上取得的用户,用户组和用户组成员.这些用户的信息只能通过你的 JIRA 服务器进行修改. https://www.cwiki.us/display ...
- Python基础--文件操作和集合
这篇博客来说一下python对文件的操作. 对文件的操作分三步: 1.打开文件获取文件的句柄,句柄就理解为这个文件 2.通过文件句柄操作文件 3.关闭文件. 现有以下文件file.txt: 我们哭了 ...
- Markdown语法笔记
1.文字和图片中怎么让图片换行? 答:在文字和图片之间加入多个空格或者直接按Tab健即可
- Deep Belief Network简介——本质上是在做逐层无监督学习,每次学习一层网络结构再逐步加深网络
from:http://www.cnblogs.com/kemaswill/p/3266026.html 1. 多层神经网络存在的问题 常用的神经网络模型, 一般只包含输入层, 输出层和一个隐藏层: ...
- Mybatis学习总结-----mybatis中refid是什么意思(十)
1.首先定义一个sql标签,一定要定义唯一id<sql id="Base_Column_List" >name,age</sql>2.然后通过id引用< ...
- POJ 1947 Rebuilding Roads 树形dp 难度:2
Rebuilding Roads Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 9105 Accepted: 4122 ...
