改善深层神经网络_优化算法_mini-batch梯度下降、指数加权平均、动量梯度下降、RMSprop、Adam优化、学习率衰减

1.mini-batch梯度下降

在前面学习向量化时，知道了可以将训练样本横向堆叠，形成一个输入矩阵和对应的输出矩阵：

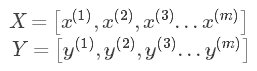
当数据量不是太大时，这样做当然会充分利用向量化的优点，一次训练中就可以将所有训练样本涵盖，速度也会较快。但当数据量急剧增大，达到百万甚至更大的数量级时，组成的矩阵将极其庞大，直接对这么大的的数据作梯度下降，可想而知速度是快不起来的。故这里将训练样本分割成较小的训练子集，子集就叫mini-batch。例如：训练样本数量m=500万，设置mini-batch=1000,则可以将训练样本划分为5000个mini-batch，每个mini-batch中含有1000个样本数据，当然，输出矩阵也要做同样的划分。这张图可以直观的理解：

在实际的训练中，会通过循环来遍历所有的mini-batch，对每一个mini-batch都会做和原来一样的步骤，即：前向传播、计算损失函数、反向传播、更新参数。

这张图可以大致反应两种梯度下降方法其损失函数的变化过程：在batch梯度下降中，由于每次训练迭代都是遍历的整个训练集，故损失函数的曲线应是一个较为平滑的下降过程，如出现明显的抖动，很大程度可能是学习率α过大。但在mini-batch梯度下降中可以看到，并不是每次迭代其损失函数都是下降的，这是因为训练集不完整的原因。但总体趋势还是下降的，抖动程度取决于设置的mini-batch的大小。

综合来说，如果训练集较小，那么直接使用batch梯度下降法，可以快速的处理整个数据集，一般来说是少于2000个样本。如果训练集再大一点，就可以考虑使用mini-batch梯度下降法，一般mini-batch的大小为64 - 512（考虑到电脑内存，设置为2的n次方，运算速度会快些）。另外，当mini-batch设置为1时，又叫做随机梯度下降法

2.指数加权平均

举个例子：下图是一年内某地气温的变化情况：

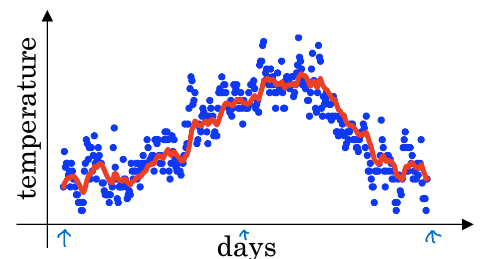
可以看到数据点比较的杂乱，但是大体趋势还是存在的。为了更好的表现气温变化情况，这里做一下这样的处理：

我们看到这个高值的β=0.98得到的曲线要平坦一些,是因为你多平均了几天的温度.所以波动更小,更加平坦.缺点是曲线向右移动,这时因为现在平均的温度值更多,所以会出现一定的延迟.对于β=0.98这个值的理解在于有0.98的权重给了原先的值,只有0.02的权重给了当日的值.我们现在将β=0.5作图运行后得到黄线,由于仅平均了两天的温度,平均的数据太少,所以得到的曲线有更多的噪声,更有可能出现异常值,但是这个曲线能更快的适应温度变化,所以指数加权平均数经常被使用. 在统计学中,它常被称为指数加权移动平均值

3.动量梯度下降

动量梯度下降（Gradient Descent with Momentum）是计算梯度的指数加权平均数，并利用该值来更新参数值。其中的动量衰减参数β一般取0.9进行一般的梯度下降将会得到图中的蓝色曲线，而使用Momentum梯度下降时，通过累加减少了抵达最小值路径上的摆动，加快了收敛，得到图中红色的曲线。当前后梯度方向一致时，Momentum梯度下降能够加速学习；前后梯度方向不一致时，Momentum梯度下降能够抑制震荡。

进行一般的梯度下降将会得到图中的蓝色曲线，由于存在上下波动，减缓了梯度下降的速度，因此只能使用一个较小的学习率进行迭代。如果用较大的学习率，结果可能会像紫色曲线一样偏离函数的范围。而使用动量梯度下降时，通过累加过去的梯度值来减少抵达最小值路径上的波动，加速了收敛，因此在横轴方向下降得更快，从而得到图中红色的曲线。当前后梯度方向一致时，动量梯度下降能够加速学习；而前后梯度方向不一致时，动量梯度下降能够抑制震荡。另外，在 10 次迭代之后，移动平均已经不再是一个具有偏差的预测。因此实际在使用梯度下降法或者动量梯度下降法时，不会同时进行偏差修正。

动量梯度下降法的形象解释

将成本函数想象为一个碗状，从顶部开始运动的小球向下滚，其中 dw，db 想象成球的加速度；而 vdw、vdb 相当于速度。小球在向下滚动的过程中，因为加速度的存在速度会变快，但是由于 β 的存在，其值小于 1，可以认为是摩擦力，所以球不会无限加速下去。最后要说一点，如果你查阅了动量梯度下降法相关资料，你经常会看到 1-β 被删除了，即

vdW[l]=βvdW[l]+dW[l]

vdb[l]=βvdb[l]+db[l]

所以V_dw缩小了1-β倍,所以你要用梯度下降最新值的话，a也要相应变化。实际上这2种方法效果都不错，只会影响到学习率a的最佳值。

4.Adagrad

Adagrad在每一个更新步骤中对于每一个模型参数Wi使用不同的学习速率ηi，

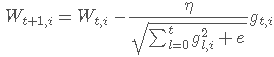
可以看到，式中学习率会除以该权值历史所有梯度的平方根，由于梯度会累加得越来越大，也就可以达到衰减学习率的效果。其中，e是一个平滑参数，为了使得分母不为0(通常e=1e−8)，另外，如果分母不开根号，算法性能会很糟糕。其优点很明显，可以使得学习率越来越小，而且每个权值根据其梯度大小不同可以获得自适应的学习率调整。其缺点在于需要计算参数梯度序列平方和，并且学习速率趋势会较快衰减达到一个非常小的值

5.RMSprop

为了缓解Adagrad学习率衰减过快，首先当然就是想到降低分子里的平方和项，RMSprop是通过将平方和变为加权平方和.也就是说平方和项随着时间不断衰减，过远的梯度将不影响学习率。

RMSprop算法，全称是root mean square prop算法，它也可以加速梯度下降，我们来看看它是如何运作的。你们知道了动量（Momentum）可以加快梯度下降，还有一个叫做RMSprop的算法，全称是root mean square prop算法，它也可以加速梯度下降，我们来看看它是如何运作的。我们来理解一下其原理。我们希望W学习速度快，而在垂直方向，也就是例子中的b方向，我们希望减缓纵轴上的摆动，所以有了和S_dw, S_db .我们希望S_dw会相对较小，所以我们要除以一个较小的数，而希望S_db又较大，所以这里我们要除以较大的数字，这样就可以减缓纵轴上的变化。因为函数的倾斜程度，在纵轴上，也就是b方向上要大于在横轴上，也就是W方向上。db的平方较大，所以S_db也会较大，而相比之下，dw会小一些，亦或平方会小一些，因此S_dw会小一些，结果就是纵轴上的更新要被一个较大的数相除，就能消除摆动，而水平方向的更新则被较小的数相除。RMSprop的影响就是你的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。还有个影响就是，你可以用一个更大学习率，然后加快学习，而无须在纵轴上垂直方向偏离。

6.Adam优化

Adam 优化算法（Adaptive Moment Estimation，自适应矩估计）基本上就是将 Momentum 和 RMSProp 算法结合在一起，通常有超越二者单独时的效果。在深度学习的历史上，包括许多知名研究者在内，提出了优化算法，并很好地解决了一些问题，但随后这些优化算法被指出并不能一般化，并不适用于多种神经网络。

RMSprop以及Adam优化算法，就是少有的经受住人们考验的两种算法，已被证明适用于不同的深度学习结构，这个算法我会毫不犹豫地推荐给你，因为很多人都试过，并且用它很好地解决了许多问题。

Adam 优化算法有很多的超参数，其中

学习率 α：需要尝试一系列的值，来寻找比较合适的；

β1：常用的缺省值为 0.9；

β2：Adam 算法的作者建议为 0.999；

ϵ：不重要，不会影响算法表现，Adam 算法的作者建议为 10−8；

β1、β2、ϵ 通常不需要调试。

7.学习率衰减

为什么要计算学习率衰减?

假设你要使用mini-batch梯度下降法，mini-batch数量不大，大概64或者128个样本，在迭代过程中会有噪音（蓝色线），下降朝向这里的最小值，但是不会精确地收敛，所以你的算法最后在附近摆动，并不会真正收敛，因为你用的α是固定值，不同的mini-batch中有噪音。

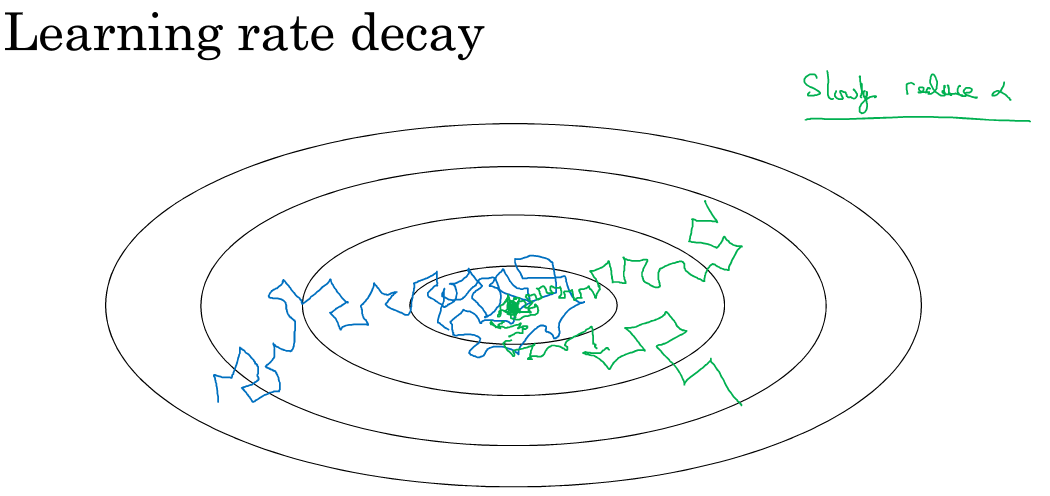
8.局部最优的问题

在低纬度的情形下，我们可能会想象到一个Cost function 如左图所示，存在一些局部最小值点，在初始化参数的时候，如果初始值选取的不得当，会存在陷入局部最优点的可能性。但是，如果我们建立一个神经网络，通常梯度为零的点，并不是如左图中的局部最优点，而是右图中的鞍点（叫鞍点是因为其形状像马鞍的形状）。

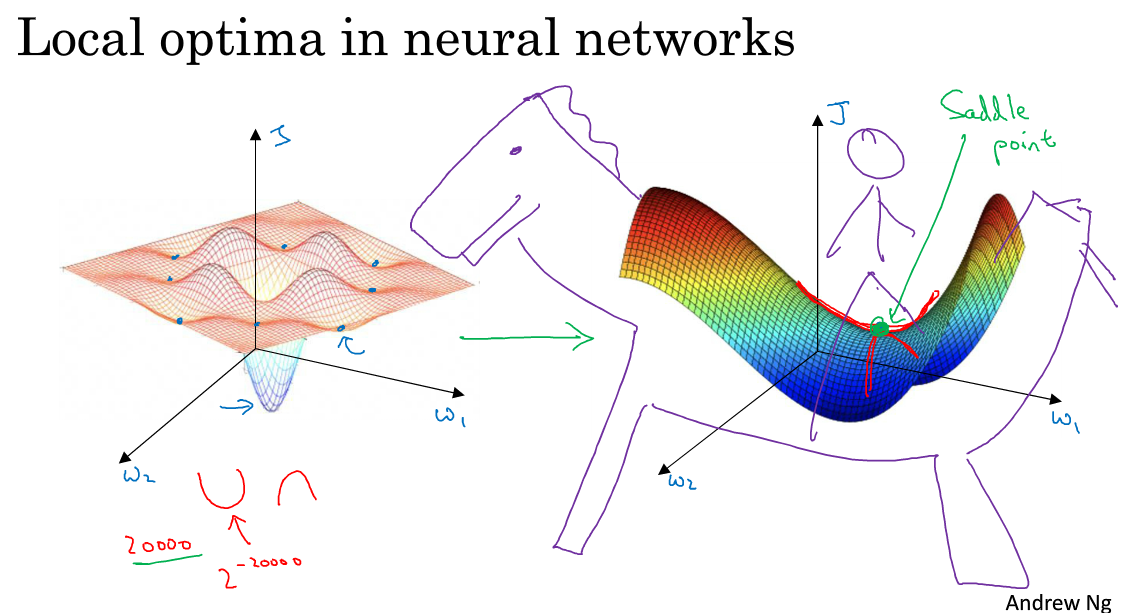
在一个具有高维度空间的函数中，如果梯度为 0，那么在每个方向，Cost function 可能是凸函数，也有可能是凹函数。但如果参数维度为 2万维，想要得到局部最优解，那么所有维度均需要是凹函数，其概率为2^−20000，可能性非常的小。也就是说，在低纬度中的局部最优点的情况，并不适用于高纬度，我们在梯度为 0 的点更有可能是鞍点。

在高纬度的情况下：

几乎不可能陷入局部最小值点；

处于鞍点的停滞区会减缓学习过程，利用如 Adam 等算法进行改善。

参考文献

[1] Optimization Algorithms优化算法

[2] 改善深层神经网络(吴恩达)_优化算法

[3] 动量梯度下降法（Gradient descent with Momentum）-吴恩达深度学习 course2 2.6笔记

[4] 局部最优的问题

[5] 卷积神经网络（五）：SGD、adagrad与RMSprop，梯度下降法总结