Python 矩阵（线性代数）

这里有一份新手友好的线性代数笔记，是和深度学习花书配套，还被Ian Goodfellow老师翻了牌。

笔记来自巴黎高等师范学院的博士生Hadrien Jean，是针对“花书”的线性代数一章，初来乍到的小伙伴可以在笔记的辅佐之下，了解深度学习最常用的数学理论，加以轻松的支配。

把理论和代码搭配食用，疗效更好。笔记里列举的各种例子，可以帮初学者用一种更直观实用的方式学好线代。开始前，你需要准备好Numpy和Python。

然后来看一下，要走怎样一个疗程——

1 标量、向量、矩阵和张量

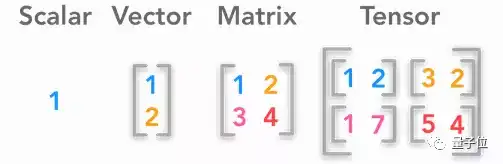△ 标量，向量，矩阵，张量 (左起)

这一课讲了向量和矩阵，以及它们的一些基础运算。另外，这里介绍了Numpy的一些相关函数，也浅浅地谈到了Broadcasting机制。

2 矩阵和向量的乘法

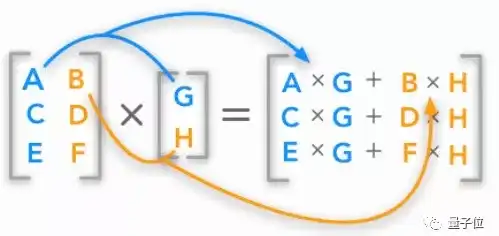△ 矩阵与向量的点乘

本小节主要讨论的是，向量和矩阵的点积，我们可以从中了解矩阵的一些属性。之后，便是用矩阵符号来创建一个线性方程组——这也是日后的学习里，经常要做的事情。

3 单位矩阵和逆矩阵

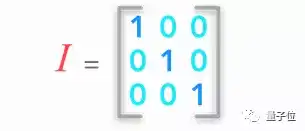△ 单位矩阵长这样

我们要了解这两种矩阵为什么重要，然后知道怎样在Numpy里和它们玩耍。另外，本小节包含用逆矩阵求解线性方程组的一个例题。

4 线性依赖与线性生成空间

线性方程组，除非无解，不然要么有唯一解，要么有无穷多解。

看着图像，我们可能更直观地了解，这件看上去理所当然的事情，背后的道理是什么。

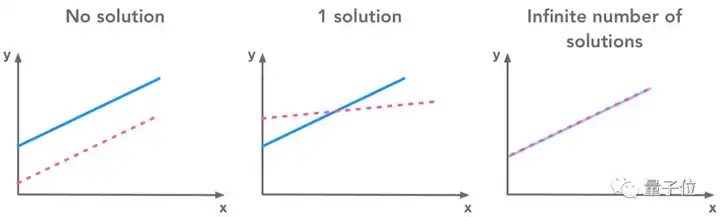△ 无解，一解，无穷多解 (左起)

回到方程组的矩阵形式，感受Gilbert Strang说的“横看成岭侧成峰”——竖看几个方程，横看一个方程里的多个系数。

然后，我们要理解什么是线性组合，还会看到关于超定和欠定方程组的几个例子。

5 范数

向量的范数是个函数，将一个向量输入，我们就得到一个正值——可以把它看做向量的长度。

范数可以用来衡量模型预测值与实际值之间的距离。

6 特殊的矩阵和向量

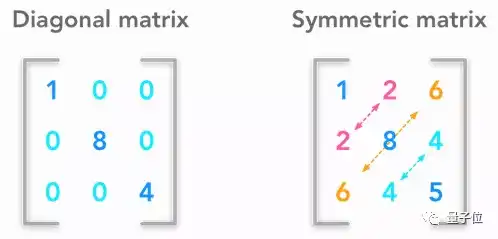△ 对角矩阵 (左) 与对称矩阵 (右)

一些矩阵和向量，会有和普通矩阵/向量不一样的有趣特性。虽然，这个小节不长，但对理解后面的内容会有帮助。

7 特征分解

这里，有线性代数的一些主要概念。我们可以对特征向量和特征值，有一个初步的了解。

大家将会看到，矩阵并不像外表那样单调，它们可以作为线性变换的工具。用一个矩阵对它的特征向量做些加工，便会得到方向相同的新向量。

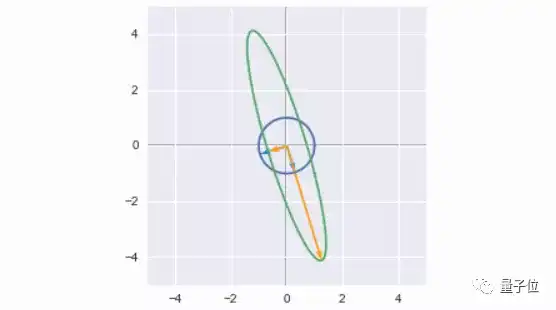△ 特征向量 (蓝箭头) ，线性变换后的向量 (黄箭头)

然后，矩阵还可以用来表示二次函数。利用矩阵的特征分解，可以找到对应函数的最大值和最小值。

坚持读到这个小节，就可以解锁用Python将线性变换可视化的操作。

8 奇异值分解 (SVD)

这是除了特征值分解之外的，另一种矩阵分解方式。SVD是将一个矩阵，分解到三个新矩阵里面。

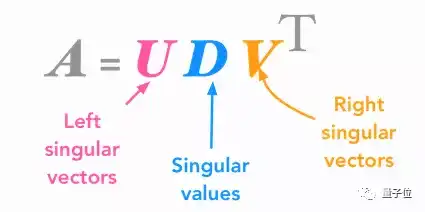△ 一分为三的矩阵A

依照“将矩阵看做空间的线性变换”这一理念，我们可以将这些新的矩阵，当做空间的子变换——变换并非一步达成，而是经过了三个分解动作。

走到这里，就可以捡起“将SVD用于图像处理”的新装备。

9 摩尔-彭若斯伪逆

在研究矩阵的路上，我们会遇到不同的风景。

并不是所有矩阵都有自己的逆矩阵。不幸之处不在于孤独，而在于逆矩阵可以用来解方程组。方程组无解的时候，也就没有逆矩阵。

△ 无解的超定方程组

不过，如果将误差最小化，我们也可以找到一个很像解的东西。伪逆便是用来找假解的。

10 迹

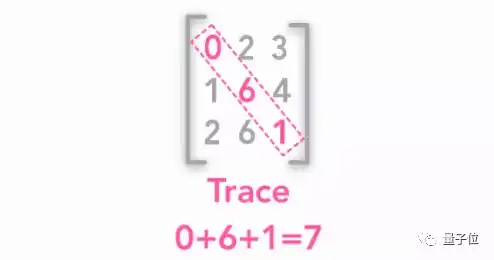△ 矩阵的迹

上图就是矩阵的迹。后面讲到主成分分析 (PCA) 的时候，会需要这个看上去不怎么厉害的东西。

11 行列式

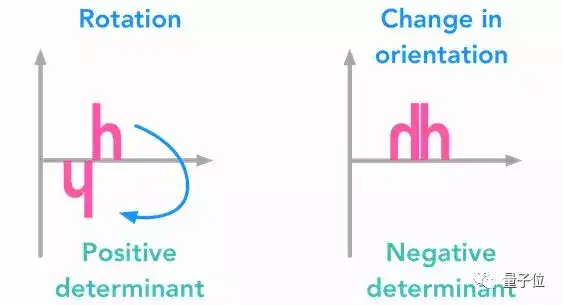△ 有正有负的行列式

行列式是一个奇妙的数值，可以告诉我们关于矩阵的很多秘密。

12 主成分分析 (PCA) 例题

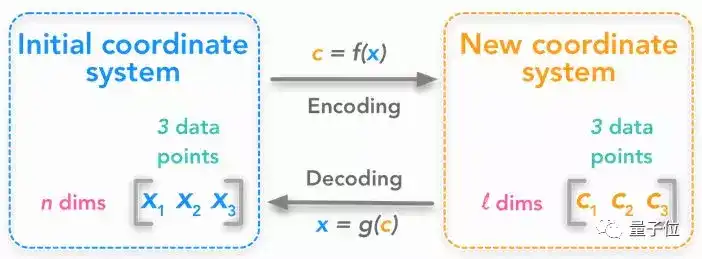△ 要找到编码与解码的方法

恭喜大家来到线性代数的最后一课。

用上前十一课传授的全部技能，便能掌握这个数据分析重要工具的使用方法。

最后说一句，这份笔记看去有几分软妹，图片配色和那些年所见的硬汉画风截然不同，相信初学者的各位也会很有食欲的。

全套笔记真容在此：
https://hadrienj.github.io/posts/

花书线代章节在此：
http://www.deeplearningbook.org/contents/linear_algebra.html