斯坦福【概率与统计】课程笔记（三）：EDA

单个定量变量的直方图表示

大家知道，定量变量是连续型变量，即不会像分类变量那样有明显的分类，那么如何将其画成直方图呢？一般来说，会将其按照某个维度来将其分组（group），举个例子。

我们有15个学生的考试成绩：88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73

如果要画成直方图，X轴是成绩，Y轴是对应的人数，那么X轴可以考虑按“每10分”作为一个group，即[0, 10), [10, 20), [20, 30), ... ,[80, 90), [90, 100)这样组织：

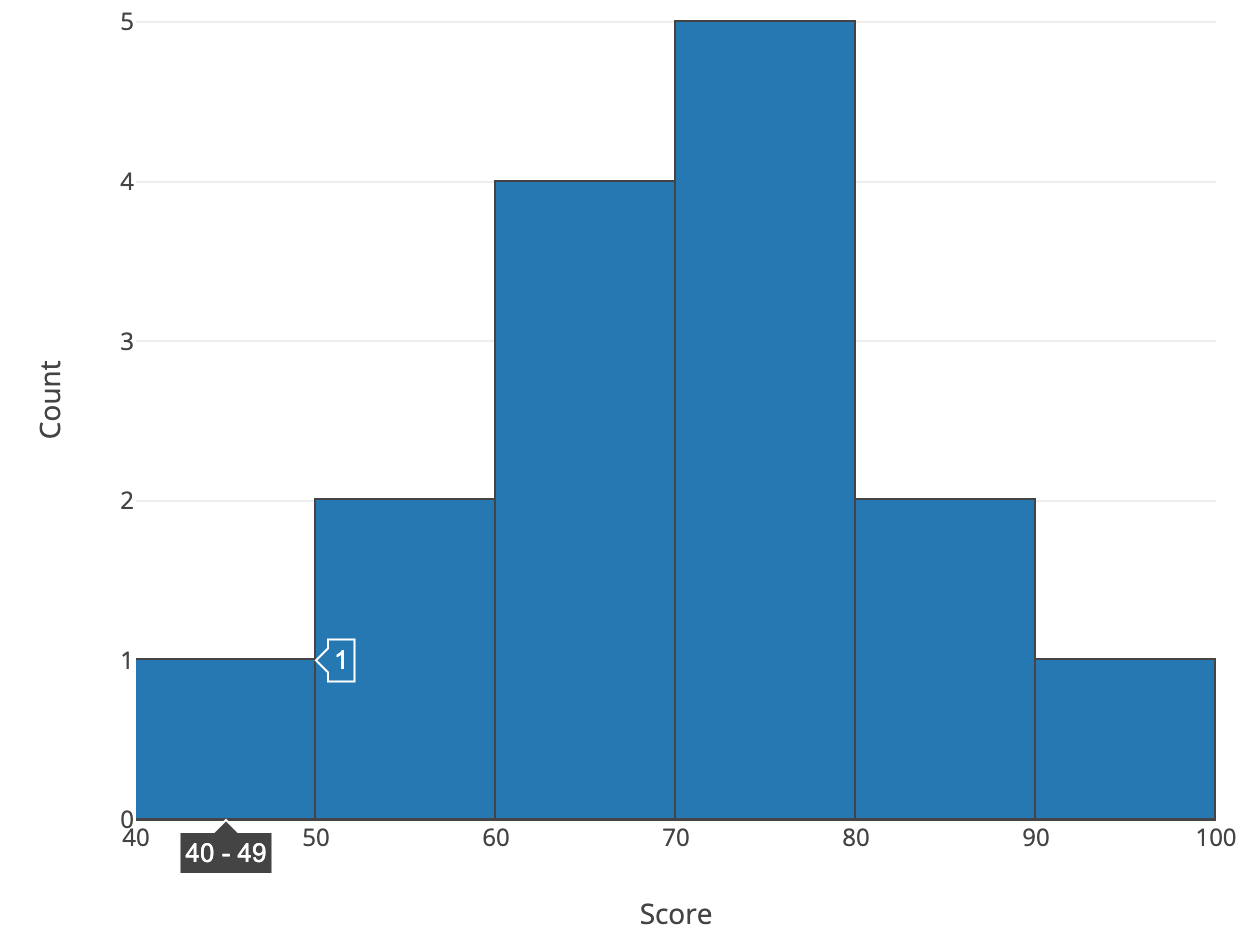
类似分类变量的柱状图，定量变量的直方图的Y轴，也可以将值（value）转换为百分比（percent）

直方图有几个重要的概念是需要掌握的，分别是：shape、center、spread、outliers

shape

shape指从直方图的整体形状来定性其分布特点，一般分为两个维度：

对称（Symmetry）/有偏（skewness）
有峰（Peakedness）/平滑 (modality)

下面分别举几个例子：

上面的直方图，首先是对称的（即Y轴左右基本对称），其次是有峰的（x=10左右的位置有个单峰值），所以是“对称、单峰值分布”

上面的直方图，也是对称的，而且是有双峰的，所以是“对称、双峰值分布”

上面的直方图，没有明显的峰值，所以是“对称、平滑分布”

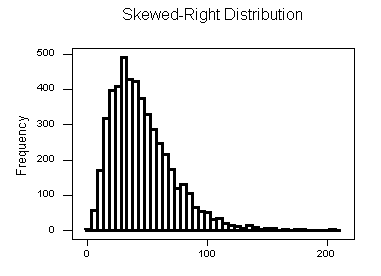
上面的直方图，可以看到右边有很长的长尾数据，所以是“有偏（右偏）、单峰值分布”

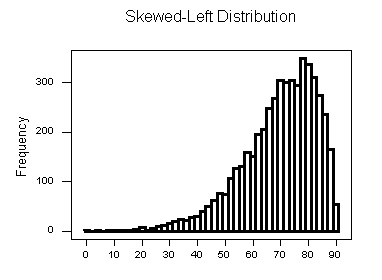
类似地，上面的直方图是“左偏、单峰值分布”

这里可能有个疑惑：为啥峰值偏左的叫右偏，而峰值偏右的叫左偏呢？实际上，这里是根据均值和中位数的相对位置来命名左或右的，下面说完center后会重新提到。

center

直方图的中心可以有很多种定义方法：

mode：即众数，是X轴上Y值最大的那一个group（即直方图上峰值最高的那一个柱子的值）
mean：即（加权）平均值，将所有值加权相加后除以总数
median：即中位数，即将所有样本排序后，所有样本的总数除以2，取中间的1个样本的值（总样本是奇数）或2个样本的值的平均数（总样本是偶数）

举个例子：

我们有15个学生的考试成绩：88, 48, 60, 51, 57, 85, 69, 75, 97, 72, 71, 79, 65, 63, 73

如果按照每10分来划分group，则直方图为：

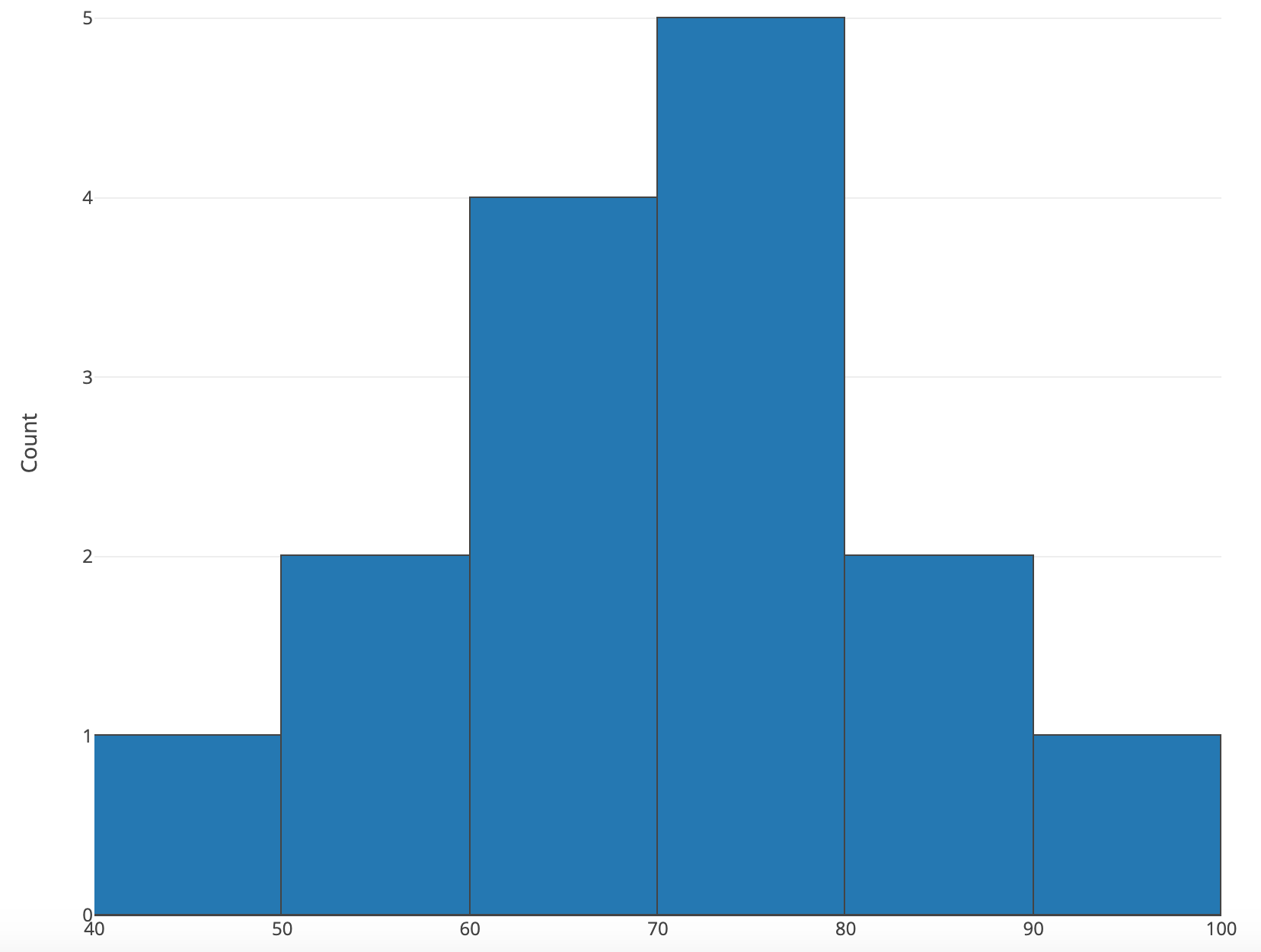
对应上图：

mode：是峰值最高的那个柱子，就是[70, 80)对应的那个柱子的值：5

mean：(88 + 48 + 60 + 51 + 57 + 85 + 69 + 75 + 97 + 72 + 71 + 79 + 65 + 63 + 73) / 15 = 70.2

median：先排序（48, 51, 57, 60, 63, 65, 69, 71, 72, 73, 75, 79, 85, 88, 97），找到中间的值：71

spread

上面提到过，左偏和有偏的问题，这里结合mean和median再进一步阐述下：

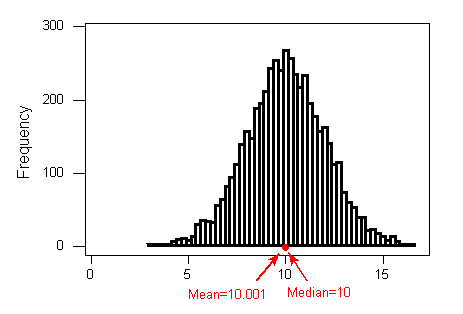
上图是一个对称分布的情况，可见：mean和median基本在一个位置上

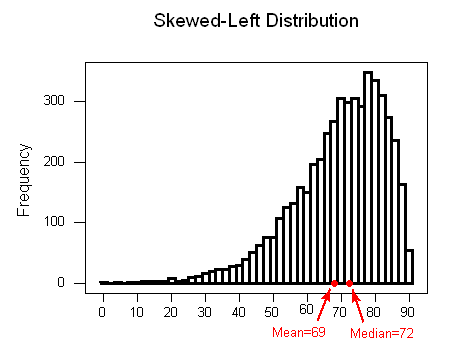
上图是一个左偏的情况，可以看到左侧有很多长尾数据，median受到了长尾数据影响，并没有出现在最高峰值附近而是向左偏移了一点点，但是平均值mean受长尾数据影响更大，其向左偏移的幅度也更大，所以相对对称分布来说，上图中mean和median都向左发生了偏移，所以这种分布叫左偏。

右偏相反理解即可

outliers

即异常值，比如下图：

最右边的值看起来很奇怪，和大部分值都不一样，所以可能会被怀疑为异常值。

一般来说，发现有异常值的时候，需要进一步分析一下其产生的原因，如果是合理的，那么需要保留；如果是不合理的，则需要过滤掉；如果是错误导致的，则需要重新计算。

mode不受异常值影响；median对异常值不敏感；而mean对异常值非常敏感！