[算法]Min_25筛

前言

本篇文章中使用的字母\(p\)，指\(\text{任意的} p \in \text{素数集合}\)

应用场景

若函数\(f(x)\)满足，

1. \(f(x)\)是积性函数
2. \(f(p)\)可以使用多项式表示。
3. 已知\(f(p)\)，要能在常数级的时间内计算\(f(p^x),x \in N^+\)。

Min_25筛可以在\(\Theta(\frac{n^{\frac{3}{4}}}{log_2n})\)的时间复杂度内计算\(f(x)\)的前缀和

或者说\(\Theta(n ^ {1 - \epsilon})\)?个人倾向上面那种。

算法

分类

\[\sum_{i=1}^n f(i)=\sum_{p=1}^nf(p),p \in prime\ + \sum_{q=1}^nf(q) ,q \notin prime
\]

prime指素数集合

辅助函数\(g(x,y)\)的构造与递推

首先线性筛出质数，线性筛就不多说了（如果您线性筛都不会建议先去学习基础算法）

我们从小到大设\(p_i\)为从小到大排列的第i个质数

例如，\(p_1=2,p_2=3,\dots\)

设素数集合为prime，i的最小质因子为\(MPF_i\) (minimal prime fact of i)。

\(||\)为或者，即\(or\); \([a]\)表示a成立是为\(1\)，否则为\(0\)

设函数\(g(x,y)\)，使得

\[g(x,y)=\sum_{i=1}^x[i\in prime\ ||\ MPF_i>p_y]f(i)
\]

考虑埃拉托斯特尼筛法，每次选出一个质数，筛掉它的倍数。

注:埃拉托斯特尼筛法的百度百科

我们发现\(g(x,y)\)有一个神奇的性质，我们的\(g(x,y)\)就是\([1,x]\)运行y次筛法以后剩余所有数之和加上所有的\(f(p),p<x\)的和。

我们所求的(prime为质数集合)

\[\sum_{i=1}^x[i\in prime]
\]

实际上等同于\(g(x,|prime|)\)，|prime|表示\([1,x]\)之内的质数集合的大小。

首先我们要了解\(g(x,y)\)的初值

\(g(x,0)\)表示所有数的和，也就是把所有数带入\(f(x)\)计算出的结果。

那么接下来就是\(g(x,y)\)的递推了。

1. \(p_y^2 > x\)。 此时埃筛的第\(j\)次没有筛去任何质数(理论上第\(y\)次应该筛掉的最小质数为\(p_y^2\))，所以\(g(x,y)=g(x,y-1)\)
2. \(p_y^2 \leq x\)。此时埃筛筛去了所有大于\(p_y\)倍的\(p_y\)的倍数，若我们从\(g(x,y-1)\)递推，显然有多计算的部分，该部分就是

\[f(p_y)\times(g(\frac{x}{p_y},y-1)-\sum_{i=1}^{y-1}f(i))
\]

表示成公式就是:

\[g(x,y) = \left\{ \begin{matrix} g(x,y-1) & p_y^2>x \\ \\ g(x,y-1)-f(p_y)\times(g(\frac{x}{p_y},y-1)-\sum_{i=1}^{y-1}f(i)) & p_y^2 \leq x\end{matrix} \right.
\]

前缀函数\(S(x,y)\)的构造与递推

好了现在我们已经有了一个辅助函数\(g(x,y)\)，但这玩意貌似一点用都没有....

我们设

\[S(x,y)=\sum_{i=1}^x[MPF_p \geq p_y]f(i)
\]

讲人话就是所有最小质因子大于等于\(p_j\)的\(f\)值之和。

如果我们要求\(\sum f(i),i \in [1,n]\)，我们要求的东西是

\[S(n,1)+f(1)
\]

鉴于所有质数对答案的贡献我们已经完成计算，它的贡献是

\[g(n,j)-\sum_{i=1}^{j-1}f(p_i)
\]

(我们要保证最小质因子大于等于\(p_j\)所以要把小于它的质数减去)

考虑合数对答案的贡献，枚举合数的最小质因子和它的出现次数，然后直接计算。

合数对答案的贡献是:

\[\sum_{i=y}^{p_i^2 \leq x} \sum_{j = 1}^{p_i^{j + 1} \leq x}S(\frac{x}{p_i^j},i+1)+f(p_{i}^{j+1})
\]

总结起来就是

\[S(x,y) = g(x,|prime|) - \sum_{i=1}^{y-1}f(p_i) + \sum_{j=y}^{p_j^2 \leq x} \sum_{k = 1}^{p_j^{k + 1} \leq x}S(\frac{x}{p_j^k},j+1)+f(p_{j}^{k+1})
\]

\(prime\)指素数集合，\(||\)表示取当前的最大质因子。

复杂度比较

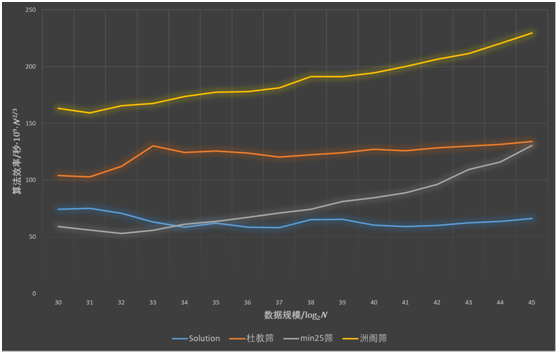
借用一下WC2019课件中的一张图片

例题

[LOJ6053]简单的函数

代码

#include <cstdio>
#include <cmath>
#define ll long long
#define MAXN 1000005
#define MOD 1000000007

long long sqrtn;

ll read(){
    ll x = 0; int zf = 1; char ch = ' ';
    while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
    if (ch == '-') zf = -1, ch = getchar();
    while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}

// the number n, cac the sum of f(i) i belongs to [1, n]
ll n;
// primes   number of primes in total
ll p[MAXN], pcnt;
// g is the function g, the sum of the f(prime).
ll g[MAXN];
// the number of the prime less the pn_i
ll pn[MAXN];
// the id of every helpful number
ll id[2][MAXN];
// prefix of p
ll prep[MAXN];

// the different value of zcfk, or (n/i)
// zcfk -> https://www.cnblogs.com/linzhengmin/p/11061244.html
ll w[MAXN], wcnt;
// is not a prime -> array in the Euler Sieve
bool np[MAXN];

// Euler Sieve
void getPrime(int n){
    np[0] = np[1] = 0;
    for (int i = 2; i <= n; ++i){
        if (!np[i]) p[++pcnt] = i, prep[pcnt] = (prep[pcnt - 1] + i) % MOD;
        for (int j = 1; j <= pcnt && i * p[j] <= n; ++j){
            np[p[j] * i] = 1;
            if (!(i % p[j])) break;
        }
    }
}

// cac function s
int S(ll x, int y){
    if (x <= 1 || p[y] > x) return 0;
    int k = (x <= sqrtn) ? id[0][x] : id[1][n / x];
    int res = (((ll)g[k] - pn[k] - prep[y - 1] + y - 1) % MOD + MOD) % MOD;
    if (y == 1) res += 2;
    for (int i = y; i <= pcnt && (ll)p[i] * p[i] <= x; ++i){
        ll p1 = p[i], p2 = (ll)p[i] * p[i];
        for (int j = 1; p2 <= x; ++j, p1 = p2, p2 *= p[i])
            (res += (1ll * S(x / p1, i + 1) * (p[i] ^ j) % MOD + (p[i] ^ (j + 1))) % MOD) %= MOD;
    }
    return res;
}

int main(){
    n = read(); sqrtn = sqrt(n); getPrime(sqrtn);
    // zcfk -> caculate function g, init array w, id
    for (ll i = 1, j; i <= n; i = j + 1){
        w[++wcnt] = n / i, j = n / w[wcnt];
        (w[wcnt] <= sqrtn) ? id[0][w[wcnt]] = wcnt : id[1][j] = wcnt;
        pn[wcnt] = (w[wcnt] - 1) % MOD, g[wcnt] = (w[wcnt] % MOD) * ((w[wcnt] + 1) % MOD) % MOD;
        if (g[wcnt] & 1) g[wcnt] = g[wcnt] + MOD;
        g[wcnt] >>= 1; g[wcnt]--;
    }
    for (int j = 1; j <= pcnt; ++j)
        for (int i = 1; i <= wcnt && p[j] * p[j] <= w[i]; ++i){
            int k = (w[i] / p[j] <= sqrtn) ? id[0][w[i] / p[j]] : id[1][n/(w[i] / p[j])];
            // minus the extra part
            (g[i] -= (ll)p[j] * (g[k] - prep[j - 1]) % MOD) %= MOD;
            // refresh pn
            (pn[i] -= pn[k] - j + 1) %= MOD;
        }
    // answer is S(n,1) plus f(1) = S(n,1) + 1
    int ans = S(n, 1) + 1;
    printf("%d\n", (ans + MOD) % MOD);
    return 0;
}