P3190 [HNOI2007]神奇游乐园

传送门

第一道插头 $dp$

由于讲不清楚所以假装各位早就会插头 $dp$ 了

首先要的是一个闭合回路，所以可以用括号表示法表示状态，然后大力分类讨论

$1.$ 没有右插头和下插头

那么我们可以啥也不干，或者加一个右插头和下插头

$2.$ 只有下插头没有右插头

那么我们可以要把下插头继续延伸，可以向下或者向右

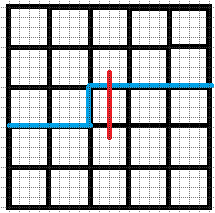
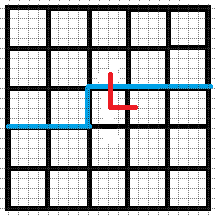
$3.$ 只有右插头没有下插头：

同理我们可以往下或者往右延伸

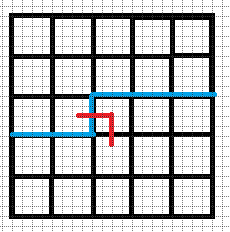
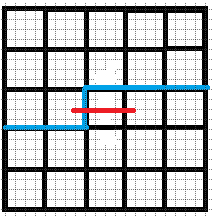
$4.$ 右插头和下插头都有：这个又要分情况讨论

　　$a.$ 插头都是左括号，那么要把两个联通还要把右边原来匹配的右括号改成左括号

　　

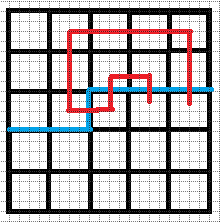
　　$b.$ 插头都是右括号，那么要把两个联通还要把左边原本匹配的左括号改成右括号

　　

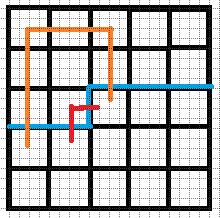
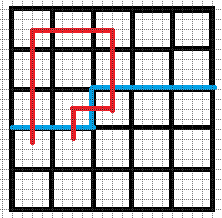
　　$c.$ 右插头是左括号，下插头是右括号，那么直接联通即可，不需要改变其他括号

　　

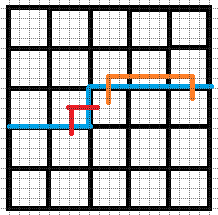
　　$d.$ 右插头是右括号，下插头是左括号，如果联通则一定形成一个闭合回路，那么如果其他地方没有插头则直接把当前状态计入答案，否则此状态不合法，不用延伸状态（右图是一种不合法状态）

　　

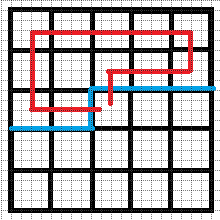
然后根据考虑到的所有状态慢慢转移即可......

因为数据比较大所以用滚动数组和哈希表维护状态，状态在加入哈希表时更新

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=3e5;
const ll INF=1e18;
int n,m,a[][],bit[],cur,pre;
ll f[][N+],Ans=-INF;
int fir[N+],from[N+],to[][N+],cntt[];//哈希表
inline void insert(int sta,ll val)//插入状态并更新f
{
    int p=sta%N;
    for(int i=fir[p];i;i=from[i])
    {
        if(to[cur][i]!=sta) continue;
        f[cur][i]=max(f[cur][i],val); return;
    }
    from[++cntt[cur]]=fir[p]; fir[p]=cntt[cur];
    to[cur][cntt[cur]]=sta; f[cur][cntt[cur]]=val;
}
void DP()
{
    cntt[cur]=; int now,down,right; ll val;
    for(int i=;i<=n;i++)//枚举行
    {
        for(int j=;j<=cntt[cur];j++) to[cur][j]<<=;//每一行末尾,状态统一左移四进制下的一位
        for(int j=;j<=m;j++)//枚举列
        {
            pre=cur; cur^=; cntt[cur]=; memset(fir,,sizeof(fir));//清空哈希表
            for(int k=;k<=cntt[pre];k++)//枚举上一行的状态
            {
                now=to[pre][k]; val=f[pre][k];
                right=(now>>bit[j-])%; down=(now>>bit[j])%;//提出插头状态
                if(!down&&!right)//没有插头
                {
                    insert(now,val);//继续没有插头
                    if(j!=m) insert(now+(<<bit[j-])+((<<bit[j])<<),val+a[i][j]);//多一个右插头和下插头
                }
                if(down&&!right)//只有下插头
                {
                    insert(now-down*(<<bit[j])+down*(<<bit[j-]),val+a[i][j]);//向下延伸
                    if(j!=m) insert(now,val+a[i][j]);//向右延伸
                }
                if(!down&&right)//只有右插头
                {
                    insert(now,val+a[i][j]);//向下延伸
                    if(j!=m) insert(now-right*(<<bit[j-])+right*(<<bit[j]),val+a[i][j]);//向右延伸
                }
                if(down==&&right==)//插头为'(('
                {
                    int cnt=;
                    for(int l=j+;l<=m;l++)//找到右边第一个和当前下插头匹配的')'
                    {
                        if((now>>bit[l])%==) cnt++;
                        if((now>>bit[l])%==) cnt--;
                        if(!cnt)
                        {
                            insert(now-(<<bit[l])-(<<bit[j-])-(<<bit[j]),val+a[i][j]);//联通并改')'为'('
                            break;
                        }
                    }
                }
                if(down==&&right==)//插头为'))'
                {
                    int cnt=;
                    for(int l=j-;l>=;l--)//找到左边第一个和当前右插头匹配的'('
                    {
                        if((now>>bit[l])%==) cnt--;
                        if((now>>bit[l])%==) cnt++;
                        if(!cnt)
                        {
                            insert(now+(<<bit[l])-((<<bit[j-])<<)-((<<bit[j])<<),val+a[i][j]);//联通并改'('为')'
                            break;
                        }
                    }
                }
                if(down==&&right==)//')('
                    insert(now-((<<bit[j-])<<)-(<<bit[j]),val+a[i][j]);//直接联通即可
                if(down==&&right==)//'()'
                    if(now==((<<bit[j])<<)+(<<bit[j-]))//当前状态只有这两个插头
                        Ans=max(Ans,val+a[i][j]);//统计答案
            }
        }
    }
}
int main()
{
    n=read(),m=read();
    for(int i=;i<=;i++) bit[i]=(i<<);
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++) a[i][j]=read();
    DP();
    printf("%lld\n",Ans);
    return ;
}