SPOJ - VLATTICE (莫比乌斯反演)

Consider a N*N*N lattice. One corner is at (0,0,0) and the opposite one is at (N,N,N). How many lattice points are visible from corner at (0,0,0) ?

A point X is visible from point Y iff no other lattice point lies on the segment joining X and Y. 
Input : 
The first line contains the number of test cases T. The next T lines contain an interger N 
Output : 
Output T lines, one corresponding to each test case. 
Sample Input : 
3 
1 
2 
5 
 
Sample Output : 
7 
19 
175 
Constraints : 
T <= 50 
1 <= N <= 1000000

题意就是给你一个三维的地图，坐标为(0,0,0)∼(n,n,n),判断有多少个坐标与原点之间的连线不经过其他的点。

思路:统计答案的点分为三类

1.坐标轴上的点(1,0,0)(0,1,0)(0,0,1) 三个

2.xoy,xoz,xoy面上的点gcd(i,j)==1; 二维很简单

3.其他点 gcd(i,j,k)==1

    

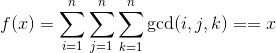
代码如下:

 #include <bits/stdc++.h>
 
 using namespace std;
 typedef long long ll;
 const int maxn = +;
 int p[maxn],mo[maxn],phi[maxn],cnt=;
 bool vis[maxn];
 void init()
 {
     mo[]=;
     phi[]=;
     for(int i=;i<=maxn-;i++){
         if(!vis[i]){
             mo[i]=-;
             phi[i]=i-;
             p[cnt++]=i;
         }
         for(int j=;j<cnt&&(ll)i*p[j]<=maxn-;j++){
             vis[i*p[j]]=true;
             if(i%p[j]==){
                 mo[i*p[j]]=;
                 phi[i*p[j]]=phi[i]*p[j];
                 break;
             }
             mo[i*p[j]]=-mo[i];
             phi[i*p[j]]=phi[i]*(p[j]-);
         }
     }
 }
 int n;
 int main()
 {
     //freopen("de.txt","r",stdin);
     init();
     int T;
     scanf("%d",&T);
     while (T--){
         scanf("%d",&n);
         ll ans = ;
         for (int i=;i<=n;++i){
             ans+=(ll)mo[i]*(n/i)*(n/i)*(n/i);
         }
         for (int i=;i<=n;++i){
             ans+=(ll)mo[i]*(n/i)*(n/i)*;
         }
         printf("%lld\n",ans+);
     }
     return ;
 }