Eversipn STT-MRAM的MJT细胞
业界一直在寻求取代SRAM。其中之一包括自旋转移力矩MRAM(STT-MRAM)。新的存储器带来了一些大胆的主张。例如STT-MRAM具有SRAM的速度和闪存的无波动性,具有无限的耐用性。
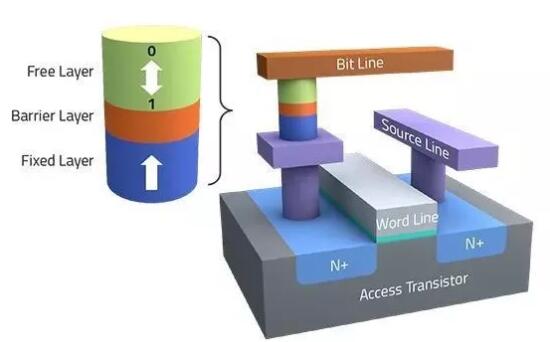
everspin已经为SSD提供SST-MRAM设备。此外一些芯片制造商正专注于嵌入式STT-MRAM,它分为两个市场,嵌入式闪存替代和缓存。
STT-MRAM是具有磁隧道结(MTJ)存储器单元的单晶体管架构。它利用电子自旋的磁性在芯片中提供非挥发性特性。写入和读取功能在MTJ单元中共享相同的并行路径。
为此STT-MRAM正准备取代嵌入式NOR闪存芯片。此外,STT-MRAM旨在取代SRAM,至少用于L3缓存。STT-MRAM正在不断发展,以更密集地嵌入到SoC中,其更小的单元尺寸,更低的待机功率要求和非易失性提供了一个引人注目的价值主张,针对用作通用板载存储器和最后级别的大得多且易变的SRAM缓存。
但STT-MRAM的速度还不足以取代SRAM用于L1和/或L2缓存,还包括稳定性。我们相信STT-MRAM,访问时间将在5ns到10ns之间饱和。当你进入L1和L2缓存时,我们相信你需要去SOT-MRAM。
类似于STT-MRAM,SOT-MRAM仍处于研发阶段。不同之处在于SOT-MRAM在器件下集成了SOT层。根据Imec,它通过在相邻的SOT层中注入面内电流来引起层的切换。
当你切换STT-MRAM,需要通过MTJ推动当前,在内存主任IMEC。在SOT-MRAM中,你有两条路径,一条用于写入,另一条用于读取。读取就像STT。你通读了MTJ。写不是通过MTJ。这是一个很大的好处,因为您可以循环设备并对其进行优化以延长使用寿命。第二大优势是速度。我司Everspin代理不同容量的MRAM存储芯片.
Eversipn STT-MRAM的MJT细胞的更多相关文章
- #include <NOIP2009 Junior> 细胞分裂 ——using namespace wxl;
题目描述 Hanks 博士是 BT (Bio-Tech,生物技术) 领域的知名专家.现在,他正在为一个细胞实 验做准备工作:培养细胞样本. Hanks 博士手里现在有 N 种细胞,编号从 1~N,一个 ...
- NOIP2009普及组细胞分裂(数论)——yhx
题目描述 Hanks 博士是 BT (Bio-Tech,生物技术) 领域的知名专家.现在,他正在为一个细胞实 验做准备工作:培养细胞样本. Hanks 博士手里现在有 N 种细胞,编号从 1~N,一个 ...
- 【OpenCV】基于kmeans的细胞检测方法
问题是这样的,有一幅经过二值化处理之后的图像,我们希望统计其中细胞的个数,和不同粘连情况的细胞个数,比如,下图中有1个细胞组成连通区域的,也有2个细胞组成连通区域的,也有更多个细胞组成连通区域的,我们 ...
- Luogu T7152 细胞(递推,矩阵乘法,快速幂)
Luogu T7152 细胞(递推,矩阵乘法,快速幂) Description 小 X 在上完生物课后对细胞的分裂产生了浓厚的兴趣.于是他决定做实验并 观察细胞分裂的规律. 他选取了一种特别的细胞,每 ...
- Luogu P1451 求细胞数量
题目描述 一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右若还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数.(1<=m,n<=100)? 输入输出格式 输 ...
- 数细胞-swust oj
数细胞(0964) 一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数.编程需要用到的队列及其相关函数已经实现,你只需要完 ...
- 【洛谷T7152】(考试题目)细胞
题面 题目描述 小 X 在上完生物课后对细胞的分裂产生了浓厚的兴趣.于是他决定做实验并 观察细胞分裂的规律. 他选取了一种特别的细胞,每天每个该细胞可以分裂出 x − 1 个新的细胞. 小 X 决定第 ...
- 细胞(cell) 矩阵快速幂
题目描述小 X 在上完生物课后对细胞的分裂产生了浓厚的兴趣.于是他决定做实验并观察细胞分裂的规律.他选取了一种特别的细胞,每天每个该细胞可以分裂出 x 1 个新的细胞.小 X 决定第 i 天向培养皿中 ...
- Python爬虫实例:爬取B站《工作细胞》短评——异步加载信息的爬取
很多网页的信息都是通过异步加载的,本文就举例讨论下此类网页的抓取. <工作细胞>最近比较火,bilibili 上目前的短评已经有17000多条. 先看分析下页面 右边 li 标签中的就是短 ...
随机推荐
- svn subvesion Branch Merge
- 认识JPA以及如何使用JPA(1)
一:JDBC是什么? JDBC统一了Java应用程序访问数据库的标准. 二:什么是JPA? JPA统一了Java应用程序使用使用ORM框架的方式. 配置文件说明: 三:使用JPA的第一个实例. 1.创 ...
- rabbitmq使用总结
rabbitmq 架构图 RabbitMQ 中的 broker 是指什么?cluster 又是指什么 broker 是指一个或多个 erlang node 的逻辑分组,且 node 上运行着 Rabb ...
- 事务管理(ACID)
目录 一.事务管理(ACID) 原子性(Atomicity) 一致性(Consistency) 持久性(Durability) 隔离性(Isolation) 二.事务隔离级别 脏读 不可复读 虚读(幻 ...
- Oracle 数据库 回滚
1.打开Flash存储的权限ALTER TABLE authorization ENABLE row movement ;2.把表还原到指定时间点flashback table authorizati ...
- FFMPEG学习----遍历所支持的封装格式
#include <stdio.h> extern "C" { #include "libavformat/avformat.h" }; int m ...
- 9. HanLP《自然语言处理入门》笔记--9.关键词、关键句和短语提取
笔记转载于GitHub项目:https://github.com/NLP-LOVE/Introduction-NLP 9. 信息抽取 信息抽取是一个宽泛的概念,指的是从非结构化文本中提取结构化信息的一 ...
- excel 2010 如何设置日期选择器
excel 中想输入很多的日期.如果每个日期都直接手动输入太过于繁琐,而且容易出错.想制作一个日期选择器,直接鼠标点选就可以了. 效果如下: 具体实现参考 http://wenku.baidu.com ...
- It is possible and safe to monitor a table DML history on sqlserver
He is my test step: In a test enviroument, I make a table "test"/ demo table:create table ...
- 在 Vs2013中查看类的内部布局
第一步:在Visual Studio中配置命令行环境(Command Prompt) 来自:https://blog.csdn.net/u013553529/article/details/77417 ...
