带你彻底理解RSA算法原理,很简单的

1. 什么是RSA

　　RSA算法是现今使用最广泛的公钥密码算法，也是号称地球上最安全的加密算法。

　　在了解RSA算法之前，先熟悉下几个术语根据密钥的使用方法，可以将密码分为对称密码和公钥密码

　　对称密码：加密和解密使用同一种密钥的方式

　　公钥密码：加密和解密使用不同的密码的方式，因此公钥密码通常也称为非对称密码。

2. RSA加密

RSA的加密过程可以使用一个通式来表达

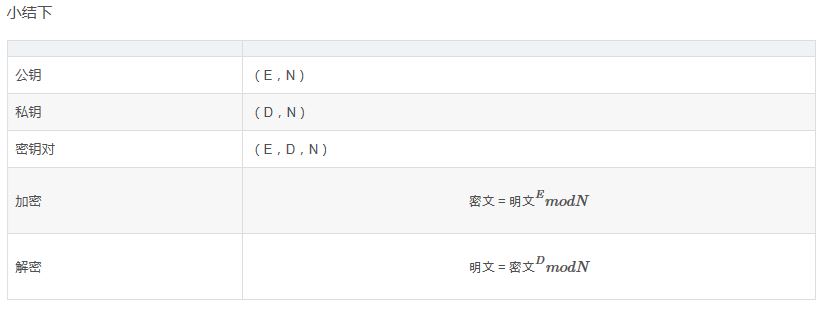
密文＝明文 E modN

也就是说RSA加密是对明文的E次方后除以N后求余数的过程。就这么简单？对，就是这么简单。

从通式可知，只要知道E和N任何人都可以进行RSA加密了，所以说E、N是RSA加密的密钥，也就是说E和N的组合就是公钥，我们用(E,N)来表示公钥

公钥＝(E,N)

不过E和N不并不是随便什么数都可以的，它们都是经过严格的数学计算得出的，关于E和N拥有什么样的要求及其特性后面会讲到。顺便啰嗦一句E是加密（Encryption）的首字母，N是数字（Number）的首字母

3. RSA解密

RSA的解密同样可以使用一个通式来表达

明文＝密文 D modN

也就是说对密文进行D次方后除以N的余数就是明文，这就是RSA解密过程。知道D和N就能进行解密密文了，所以D和N的组合就是私钥

私钥＝(D,N)

从上述可以看出RSA的加密方式和解密方式是相同的，加密是求“E次方的mod N”;解密是求“D次方的mod N” 此处D是解密（Decryption）的首字母；N是数字（Number）的首字母。

4. 生成密钥对

既然公钥是（E，N），私钥是（D，N）所以密钥对即为（E，D，N）但密钥对是怎样生成的？步骤如下：

求N
求L（L为中间过程的中间数）
求E
求D

4.1 求N

准备两个质数p，q。这两个数不能太小，太小则会容易破解，将p乘以q就是N

N=p∗q

4.2 求L

L 是 p－1 和 q－1的最小公倍数，可用如下表达式表示

L=lcm（p－1，q－1）

其中，[数] lowest common multiple (LCM) 最小公倍数

4.3 求E

E必须满足两个条件：E是一个比1大比L小的数，E和L的最大公约数为1 用gcd(X,Y)来表示X，Y的最大公约数则E条件如下：

1 < E < L

gcd（E，L）=1

abbr. 最大公约数（greatest common divisor）；

之所以需要E和L的最大公约数为1是为了保证一定存在解密时需要使用的数D。现在我们已经求出了E和N也就是说我们已经生成了密钥对中的公钥了。

4.4 求D

数D是由数E计算出来的。D、E和L之间必须满足以下关系：

1 < D < L

E＊D mod L ＝ 1

只要D满足上述2个条件，则通过E和N进行加密的密文就可以用D和N进行解密。简单地说条件2是为了保证密文解密后的数据就是明文。现在私钥自然也已经生成了，密钥对也就自然生成了。

5 实践下吧

我们用具体的数字来实践下RSA的密钥对对生成，及其加解密对全过程。为方便我们使用较小数字来模拟。

5.1 求N

我们准备两个很小对质数， p ＝ 17 q ＝ 19 N ＝ p ＊ q ＝ 323

5.2 求L

L ＝ lcm（p－1， q－1）＝ lcm(16，18）＝ 144 144为16和18对最小公倍数

5.3 求E

求E必须要满足2个条件：

1 < E < L ，

gcd（E，L）=1

即1 < E < 144，

gcd（E，144）＝ 1 E和144互为质数，

5显然满足上述2个条件 （实际上 7、11等，也满足以上 2 个条件。） 故E ＝ 5

此时公钥=(E，N）＝（5，323）

5.4 求D

求D也必须满足2个条件：

1 < D < L，

E＊D mod L ＝ 1

即1 < D < 144，

5 ＊ D mod 144 ＝ 1

显然当D＝ 29 时满足上述两个条件

1 < 29 < 144

5＊29 mod 144 ＝ 145 mod 144 ＝ 1

此时私钥＝（D，N）＝（29，323）

5.5 加密

准备的明文必须是小于N的数，因为加密或者解密都要mod N其结果必须小于N

假设明文＝ 123 则密文＝明文 E modN＝123 5 mod323=225

5.6 解密

明文＝密文 D modN＝225 29 mod323=123 解密后的明文为123。

好了至此RSA的算法原理已经讲解完毕.

参考文档： https://blog.csdn.net/dbs1215/article/details/48953589