PAT甲级——A1131 Subway Map【30】

In the big cities, the subway systems always look so complex to the visitors. To give you some sense, the following figure shows the map of Beijing subway. Now you are supposed to help people with your computer skills! Given the starting position of your user, your task is to find the quickest way to his/her destination.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 100), the number of subway lines. Then N lines follow, with the i-th (,) line describes the i-th subway line in the format:

M S[1] S[2] ... S[M]

where M (≤ 100) is the number of stops, and S[i]'s (,) are the indices of the stations (the indices are 4-digit numbers from 0000 to 9999) along the line. It is guaranteed that the stations are given in the correct order -- that is, the train travels between S[i] and S[i+1] (,) without any stop.

Note: It is possible to have loops, but not self-loop (no train starts from S and stops at S without passing through another station). Each station interval belongs to a unique subway line. Although the lines may cross each other at some stations (so called "transfer stations"), no station can be the conjunction of more than 5 lines.

After the description of the subway, another positive integer K (≤ 10) is given. Then K lines follow, each gives a query from your user: the two indices as the starting station and the destination, respectively.

The following figure shows the sample map.

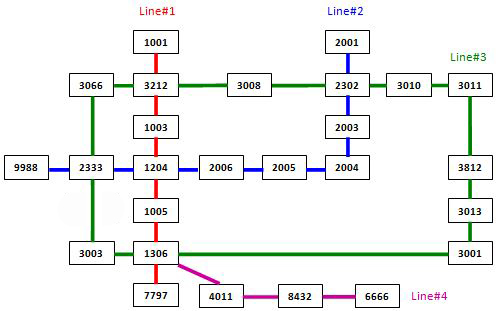
Note: It is guaranteed that all the stations are reachable, and all the queries consist of legal station numbers.

Output Specification:

For each query, first print in a line the minimum number of stops. Then you are supposed to show the optimal path in a friendly format as the following:

Take Line#X1 from S1 to S2.
Take Line#X2 from S2 to S3.
......

where Xi's are the line numbers and Si's are the station indices. Note: Besides the starting and ending stations, only the transfer stations shall be printed.

If the quickest path is not unique, output the one with the minimum number of transfers, which is guaranteed to be unique.

Sample Input:

4
7 1001 3212 1003 1204 1005 1306 7797
9 9988 2333 1204 2006 2005 2004 2003 2302 2001
13 3011 3812 3013 3001 1306 3003 2333 3066 3212 3008 2302 3010 3011
4 6666 8432 4011 1306
3
3011 3013
6666 2001
2004 3001

Sample Output:

2
Take Line#3 from 3011 to 3013.
10
Take Line#4 from 6666 to 1306.
Take Line#3 from 1306 to 2302.
Take Line#2 from 2302 to 2001.
6
Take Line#2 from 2004 to 1204.
Take Line#1 from 1204 to 1306.
Take Line#3 from 1306 to 3001.

题⽬⼤意：找出⼀条路线，使得对任何给定的起点和终点，可以找出中途经停站最少的路线；如果经

停站⼀样多，则取需要换乘线路次数最少的路线～

【很简单的，别跑^_^】

分析：⼀遍DFS即可～DFS过程中要维护两个变量：minCnt-中途经停的最少的站; minTransfer-需要换乘

的最⼩次数～

0.可以这样计算出⼀条线路的换乘次数：在line[10000][10000]的数组中保存每两个相邻站中间的线路是

⼏号线～从头到尾遍历最终保存的路径，preLine为前⼀⼩段的线路编号，如果当前的结点和前⼀个结

点组成的这条路的线路编号和preLine不同，说明有⼀个换乘，就将cnt+1，最后遍历完累加的cnt即是

换乘的次数～ 

update：由于新的PAT系统中会显示原解法有⼀个测试⽤例内存超限，考虑到line[10000][10000]存储的

⽅式太暴⼒了，所以将line换成了unordered_map<int, int> line存储的⽅式，第⼀个int⽤来存储线路，

每次将前四位存储第⼀个线路，后四位存储第⼆个线路，使⽤a[i-1]*10000+a[i]的⽅式存储，第⼆个int

⽤来保存两个相邻中间的线路是⼏号线～

1.可以这样计算出⼀条线路中途停站的次数：在dfs的时候有个变量cnt，表示当前路线是所需乘的第⼏

个站，每次dfs时候将cnt+1表示向下遍历⼀层～cnt就是当前中途停站的次数～

2.可以这样输出结果：和计算线路换乘次数的思路⼀样，每当preLine和当前Line值不同的时候就输出

⼀句话～保存preTransfer表示上⼀个换乘站，最后不要忘记输出preTransfer和最后⼀个站之间的路即使

最后⼀个站并不是换乘站～

喵呜～

 #include <iostream>
 #include <vector>
 #include <unordered_map>
 using namespace std;
 vector<int> route[];
 int visit[], minCnt, minTra, n, m, k, start, end1;
 unordered_map<int, int>line;
 vector<int>path, tempPath;
 int transferCnt(vector<int>a)
 {
     int cnt = -, preLine = ;
     for (int i = ; i < a.size(); ++i)
     {
         if (line[a[i - ] *  + a[i]] != preLine)
         {
             cnt++;//换乘了
             preLine = line[a[i - ] *  + a[i]];
         }
     }
     return cnt;
 }
 void DFS(int node, int cnt)
 {
     if (node == end1 && (cnt < minCnt || (cnt == minCnt && transferCnt(tempPath) < minTra)))
     {
         minCnt = cnt;
         minTra = transferCnt(tempPath);
         path = tempPath;
     }
     if (node == end1)return;
     for (int i = ; i < route[node].size(); ++i)
     {
         if (visit[route[node][i]] == )//未遍历过
         {
             visit[route[node][i]] = ;
             tempPath.push_back(route[node][i]);//保存可行路径
             DFS(route[node][i], cnt + );//经过一站
             visit[route[node][i]] = ;
             tempPath.pop_back();//使用回溯法
         }
     }
 }
 int main()
 {
     cin >> n;
     for (int i = ; i <= n; ++i)
     {
         cin >> m >> start;
         for (int j = ; j < m; ++j)
         {
             cin >> end1;
             route[start].push_back(end1);
             route[end1].push_back(start);
             line[start *  + end1] = line[end1 *  + start] = i;//用pot1*10000+pot来表示这两个站是可行的
             start = end1;
         }
     }
     cin >> k;
     while (k--)
     {
         cin >> start >> end1;
         minCnt = minTra = INT32_MAX-;
         tempPath.clear();
         tempPath.push_back(start);
         visit[start] = ;
         DFS(start, );
         visit[start] = ;
         cout << minCnt << endl;
         int preLine = , preTra = start;
         for (int i = ; i < path.size(); ++i)
         {
             if (line[path[i - ] *  + path[i]] != preLine)//换乘了
             {
                 if (preLine != )
                     printf("Take Line#%d from %04d to %04d.\n", preLine, preTra, path[i - ]);
                 preLine = line[path[i - ] *  + path[i]];
                 preTra = path[i - ];
             }
         }
         printf("Take Line#%d from %04d to %04d.\n", preLine, preTra, end1);
     }
     return ;
 }