吴裕雄--天生自然Numpy库学习笔记：NumPy 线性代数

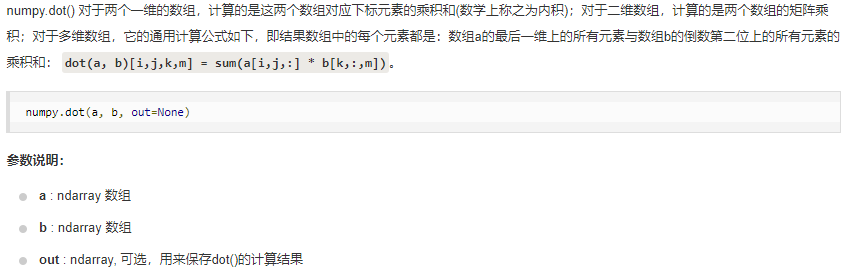
import numpy.matlib
import numpy as np

a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]])
print(np.dot(a,b))

numpy.vdot() 函数是两个向量的点积。 如果第一个参数是复数，那么它的共轭复数会用于计算。 如果参数是多维数组，它会被展开。
import numpy as np 

a = np.array([[1,2],[3,4]])
b = np.array([[11,12],[13,14]]) 

# vdot 将数组展开计算内积
print (np.vdot(a,b))
计算式为：
1*11 + 2*12 + 3*13 + 4*14 = 130

numpy.inner() 函数返回一维数组的向量内积。对于更高的维度，它返回最后一个轴上的和的乘积。
import numpy as np 

print (np.inner(np.array([1,2,3]),np.array([0,1,0])))
# 等价于 1*0+2*1+3*0

import numpy as np
a = np.array([[1,2], [3,4]]) 

print ('数组 a：')
print (a)
b = np.array([[11, 12], [13, 14]]) 

print ('数组 b：')
print (b)

print ('内积：')
print (np.inner(a,b))

内积计算式为：
1*11+2*12, 1*13+2*14
3*11+4*12, 3*13+4*14

numpy.matmul 函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积，但如果任一参数的维数大于2，则将其视为存在于最后两个索引的矩阵的栈，并进行相应广播。
另一方面，如果任一参数是一维数组，则通过在其维度上附加 1 来将其提升为矩阵，并在乘法之后被去除。
对于二维数组，它就是矩阵乘法：
import numpy.matlib
import numpy as np 

a = [[1,0],[0,1]]
b = [[4,1],[2,2]]
print (np.matmul(a,b))

二维和一维运算：
import numpy.matlib
import numpy as np 

a = [[1,0],[0,1]]
b = [1,2]
print (np.matmul(a,b))
print (np.matmul(b,a))

维度大于二的数组 ：
import numpy.matlib
import numpy as np 

a = np.arange(8).reshape(2,2,2)
b = np.arange(4).reshape(2,2)
print (np.matmul(a,b))

numpy.linalg.det() 函数计算输入矩阵的行列式。
行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵，它是左上和右下元素的乘积与其他两个的乘积的差。
换句话说，对于矩阵[[a，b]，[c，d]]，行列式计算为 ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。
import numpy as np
a = np.array([[1,2], [3,4]]) 

print (np.linalg.det(a))

import numpy as np

b = np.array([[6,1,1], [4, -2, 5], [2,8,7]])
print (b)
print (np.linalg.det(b))
print (6*(-2*7 - 5*8) - 1*(4*7 - 5*2) + 1*(4*8 - -2*2))

numpy.linalg.solve() 函数给出了矩阵形式的线性方程的解。
考虑以下线性方程：
x + y + z = 6
2y + 5z = -4
2x + 5y - z = 27
可以使用矩阵表示为：

numpy.linalg.inv() 函数计算矩阵的乘法逆矩阵。
逆矩阵（inverse matrix）：设A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注：E为单位矩阵。
import numpy as np 

x = np.array([[1,2],[3,4]])
y = np.linalg.inv(x)
print (x)
print (y)
print (np.dot(x,y))

现在创建一个矩阵A的逆矩阵:
import numpy as np 

a = np.array([[1,1,1],[0,2,5],[2,5,-1]]) 

print ('数组 a：')
print (a)
ainv = np.linalg.inv(a) 

print ('a 的逆：')
print (ainv)

print ('矩阵 b：')
b = np.array([[6],[-4],[27]])
print (b)

print ('计算：A^(-1)B：')
x = np.linalg.solve(a,b)
print (x)
# 这就是线性方向 x = 5, y = 3, z = -2 的解

结果也可以使用以下函数获取：
x = np.dot(ainv,b)