【BZOJ-2177】曼哈顿最小生成树 Kruskal + 树状数组

2177: 曼哈顿最小生成树

Time Limit: 10 Sec  Memory Limit: 259 MB
Submit: 190  Solved: 77
[Submit][Status][Discuss]

Description

平面坐标系xOy内，给定n个顶点V = (x , y)。对于顶点u、v，u与v之间的距离d定义为|xu – xv| + |yu – yv| 你的任务就是求出这n个顶点的最小生成树。

Input

第一行一个正整数n，表示定点个数。 
接下来n行每行两个正整数x、y，描述一个顶点。

Output

只有一行，为最小生成树的边的距离和。

Sample Input

4
1 0
0 1
0 -1
-1 0

Sample Output

6

HINT

对于100%的数据n <= 50000；

0 <= x, y <= 100000。

Source

Solution

曼哈顿距离最小生成树裸题

那么来说一下曼哈顿距离最小生成树

首先给出$N$个点，求普通的最小生成树，Kruskal的时间复杂度是$O(MlogN)$，显然$M$的级别是$N^{2}$的，但曼哈顿距离最小生成树能做到$O(NlogN)$

先考虑最小生成树的一个性质：如果图中存在一个环，那么把环上最大边删掉，得到的与不删环的MST权和是一样的

利用这个性质，我们构建边的时候，就能大大减少边的数量

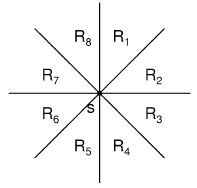
考虑现在在一个点$S$,可以从这个点为中心，把平面分成8份

然后我们发现，在一个象限中，点$S$至多和一个点相连的边是有用的。

先说一个自己的理解但不是很详尽的证明；

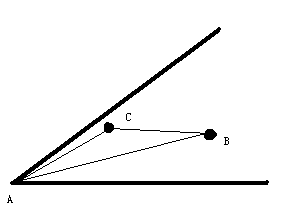
我们考虑，如果全都连边，大概是这样的情况，但是我们发现，$|AC|<|AB| && |CB|<|AB|$

那么考虑环切定理，这样，边AB是可以删去的，所以很容易理解每个点只需要连象限中离他最近的点即可

证明：

八个扇形区域是对称的，我们只考虑R₁。

把s看作原点，R₁里面的点(x,y)都满足：

x≥0,

y>x.

考察R₁里面两个点p和q，不失一般性设x_p≤x_q。

1.       y_p≤y_q

|PQ|=x_q+y_q-(x_p+x_q)

|SP|=x_p+y_p

|SQ|=x_q+y_q

所以|PQ|=|SQ|-|SP|≤|SQ|

可见当y_p≤y_q时，|PQ|不是三角形SPQ的最长边。（在曼哈顿距离下的“最长”）

2.       y_p>y_q­

0≤x_p≤x_q≤y_q<y_p

|PQ|=x_q-x_p+y_p-y_q

|SP|=x_p+y_p

|SQ|=x_q+y_q

即|PQ|= (y_p-x_p)+(x_q-y_q)

因为x_q≤y_q，所以|PQ|≤yp-xp≤yp≤xp+yp=|SP|

也就是说，当y_p>y_q时，|PQ|仍然不是三角形SPQ的最长边。（曼哈顿距离意义下的“最长”）

综上，|PQ|无论如何也不可能是三角形SPQ的最长边。即：在环<s, p, q>中，最大边只可能是|SP|和|SQ|。根据“环切”性质，我们把|SP|和|SQ|中的较长边删除即可。

假设R₁里面有m个顶点：P₁, P₂, …, P_m，假设距离s最近的点是P_k，那么只要在S和P_k之间连边即可。

所谓距离s最近的点，实际上就是x_k+y_k最小的点。

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
int read()
{
    int x=,f=; char ch=getchar();
    while (ch<'' || ch>'') {if (ch=='-') f=-; ch=getchar();}
    while (ch>='' && ch<='') {x=x*+ch-''; ch=getchar();}
    return x*f;
}
#define MAXN 100010
int N;
struct PointNode{int x,y,id;}P[MAXN];
bool cmpP(PointNode A,PointNode B) {return A.x!=B.x? A.x<B.x : A.y<B.y;}
struct UnionFind
{
    int Fa[MAXN];
    void Init() {for (int i=; i<=N; i++) Fa[i]=i;}
    int Find(int x) {if (Fa[x]==x) return x; else return Fa[x]=Find(Fa[x]);}
    bool Merge(int x,int y) {int f1=Find(x),f2=Find(y); if (f1==f2) return ; Fa[f1]=f2; return ;}
}uf;
int Dis(PointNode A,PointNode B) {return abs(A.x-B.x)+abs(A.y-B.y);}
struct EdgeNode{int to,val,from;}edge[MAXN<<];
int cnt;
void AddEdge(int u,int v,int w) {cnt++; edge[cnt].from=u; edge[cnt].to=v; edge[cnt].val=w;}
bool cmpE(EdgeNode A,EdgeNode B) {return A.val<B.val;}
int lowbit(int x) {return x&-x;}
struct BITNode{int minn,pos; void init() {minn=0x7fffffff; pos=-;}}bit[MAXN];
void Update(int x,int val,int pos)
{
    for (int i=x; i; i-=lowbit(i))
        if (val<bit[i].minn) bit[i].minn=val,bit[i].pos=pos;
}
int Query(int x,int M)
{
    int minn=0x7fffffff,pos=-;
    for (int i=x; i<=M; i+=lowbit(i))
        if (bit[i].minn<minn) minn=bit[i].minn,pos=bit[i].pos;
    return pos;
}
int num,Ans;
void MST()
{
    int a[MAXN],b[MAXN];
    for (int k=; k<=; k++)
        {
            if (k== || k==) for (int i=; i<=N; i++) swap(P[i].x,P[i].y);
                else if (k==) for (int i=; i<=N; i++) P[i].x=-P[i].x;
            stable_sort(P+,P+N+,cmpP);
            for (int i=; i<=N; i++)
                a[i]=b[i]=P[i].y-P[i].x;
            stable_sort(b+,b+N+);
            int M=unique(b+,b+N+)-b-;
            for (int i=; i<=M; i++) bit[i].init();
            for (int i=N; i>=; i--)
                {
                    int pos=lower_bound(b+,b+M+,a[i])-b;
                    int ans=Query(pos,M);
                    if (ans!=-) AddEdge(P[i].id,P[ans].id,Dis(P[i],P[ans]));
                    Update(pos,P[i].x+P[i].y,i);
                }
        }
    stable_sort(edge+,edge+cnt+,cmpE);
    uf.Init();
    for (int i=; i<=cnt; i++)
        {
            int u=edge[i].from,v=edge[i].to;
            if (uf.Merge(u,v)) Ans+=edge[i].val,num++;
            if (num==N-) break;
        }
}
int main()
{
    N=read();
    for (int i=; i<=N; i++) P[i].x=read(),P[i].y=read(),P[i].id=i;
    MST();
    printf("%d\n",Ans);
    return ;
}

感觉很愚蠢的代码