Reflect(欧拉函数）

Reflect

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 288    Accepted Submission(s): 174

Problem Description

We send a light from one point on a mirror material circle,it reflects N times and return the original point firstly.Your task is calcuate the number of schemes.

 

Input

First line contains a single integer T(T≤10) which denotes the number of test cases.

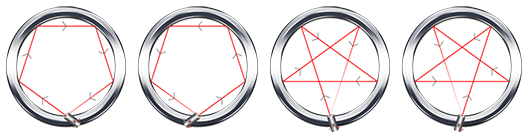
For each test case, there is an positive integer N(N≤106).

 

Output

For each case, output the answer.

 

Sample Input

1
4

 

Sample Output

4

 

Source

BestCoder Round #54 (div.2)

#include<bits/stdc++.h>
using namespace std;
const int M = 1e6+10 ;
int phi[M] , prime[M] ;

int Euler () {
        for (int i = 2 ; i < M ; i ++) {
                if (!phi[i]) {
                        phi[i] = i-1 ;
                        prime[ ++prime[0] ] = i ;
                }
                for (int j = 1 ; j <= prime[0] && 1ll*i*prime[j] < M ; j ++) {
                        if (i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1) ;
                        else {
                                phi[i * prime[j] ] = phi[i] * prime[j] ;
                                break ;
                        }
                }
        }
}

int main () {
        Euler () ;
        int T ;
        scanf ("%d" , &T) ;
        int n ;
        while (T --) {
                scanf ("%d" , &n) ;
                printf ("%d\n" , phi[n+1]) ;
        }
        return 0 ;
}

虽然说标签上写着欧拉，但在分析出之前，并没有什么用。

一开始我是这么想的，如果当前的点数为n。cnt = 0 ;

那么我枚举 i = 1~n/2，如果n % i == 0 ，那么当前这种情况肯定是不行的（这里i可以认为是你隔了i个点连线）,其余情况，我都令cnt++

因为我想如果当前的间隔点数>n/2 , 那么相当于前一半的对称，我最后答案只要cnt*2就ok了。

个人现在仍觉得蛮对的。（但实际上wa了）

但进一步分析：

2θ * n = 2*k*pi ;

θ = k/n * pi ;

所以理论上来说只要k <= n ,都是能回到圆点的。但题目要求要“恰好”

然后我们假设存在三个正整数k，a，b，k=a+b。

那么你很容易证明若 k 与 a 互质 ， 则k 必与 b互质；同样的，k 若与 a 不互质，则k 与 b必定不互质。

所以我在枚举 i = 1~n/2的过程中，若枚举到一个数x ， n%x == 0 ， 那么 n % （n-x） == 0 ，

而且你会发现x ， 和n - x就是个对称的过程。

所以其实我在干的过程就是 寻找与n互质的数的个数 。

所以用欧拉函数完全没问题。