浅谈 LCA

LCA问题

一.概述：

　　在图论与计算科学中，两个节点 v 与 w 在有向无环图( directed acyclic graph , DAG )或树中的最近公共祖先(Lowest common anccestor , LCA ) 是这两个节点 v 与 w 的深度最深的祖先。我们定义，该深度最深的节点为 v 与 w 的最近公共最先，即LCA 。

例如，在下图中

LCA ( A , B ) = F , LCA ( A , G ) = C , LCA ( B , D ) = C , LCA ( C , G ) = C ;

[ATTENTION]:两个节点的LCA在两点间的路径上。

二.求解方法

　　方法一：

　　　　将LCA问题转化为RMQ问题(区间最值问题)。

　　　　1).从任意一个节点开始，对图进行深度优先遍历，记录每个节点的欧拉序，深度，第一次被遍历fst[]时间等信息。

　　　　2).将每个节点的深度按照欧拉序列加入一个数组中，即每次经过一个节点时，都将其加入数组。

　　　　3).如果fst[ v ] < fst[ u ] ,则LCA( v , u ) = RMQ ( fst[ v ] , fst[ u ] )

　　　　　  如果fst[ v ] > fst[ u ] ,则LCA( v , u ) = RMQ ( fst[ u ] , fst[ v ] )

　　　　以上就是主要思路，下面举个栗子：

　　　　

　　　　

　　　　当查询A 与 D 的 LCA 时 ， LCA ( A , D ) = RMQ ( fst[ D ] , fst[ A ] )

　　　　 即，区间 [ fst[ D ] , fst[ A ] ] 的深度最小值 , 这段区间[ 2 , 7 ] ，(2 ，1 ，2 ，1 ，2 ，3)中最小值是1，1对C应的节点是C，则A，D的LCA是C 。

　　　　 [ATTENTION]:区间最值的关键字是深度.

　　　　 那么现在的问题就是解决RMQ问题，通常使用ST算法(RMQ问题之ST算法)或线段树解决,本文使用线段树解决这个问题。

　　　　 核心代码&注释：

 inline void Add_Edge ( int x , int y , int _val ){//邻接表建图
          e[ ++cnt ].to = y ;
          e[ cnt ].val = _val ;
          e[ cnt ].next = head[ x ] ;
          head[ x ] = cnt ;
 }

 void Build_Tree ( int x , int y , int i ) {//线段树建树
          tr[ i ].l = x ; tr[ i ].r = y ;
          if ( x==y ) tr[ i ].mintr = dep[ x ] , tr[ i ].pos = x ;//按照深度建树
          else {
                   QAQ mid = ( tr[ i ].l + tr[ i ].r ) >> ;
                  Build_Tree ( x , mid , i<<);
                  Build_Tree ( mid+ , y , i<<|);
                  if (tr[i<<].mintr > tr[i<<|].mintr )//tr[].mintr表示这个区间最小值 ，tr[].pos表示最小值所在位置
                           tr[ i ].pos = tr[i<<|].pos,tr[ i ].mintr = tr[i<<|].mintr;
                  else
                          tr[ i ].pos = tr[ i<< ].pos,tr[ i ].mintr = tr[ i<< ].mintr;
          }

 }

 void DFS ( int x , int depth ) {
          vis[ x ] = true ;
          ver[ ++dfs_num ] = x ; //欧拉序
          fst[ x ] = dfs_num ; //第一次出现位置
          dep[ dfs_num ] = depth ;//该节点深度
          for ( int i=head[ x ] ; i ; i=e[i].next ) {
                   int temp = e[ i ].to ;
                   if ( !vis[ temp ] ){
                            DFS ( temp , depth +  ) ;
                            ver[ ++dfs_num ] = x ;
                            dep[ dfs_num ] = depth ;
                  }
          }
 }

 void Query_Min ( int q , int w , int i ) {
          if(q <= tr[i].l && w >= tr[i].r ){
                   if (tr[ i ].mintr < min_val ){
                            min_val = tr[i].mintr ;// 记录最小值
                            min_pos = tr[i].pos ;// 记录最小值所在位置
                   }
          }
          else {
                   QAQ mid = (tr[i].l + tr[i].r ) >> ;
                   if(q > mid) {
                           Query_Min ( q , w , i <<  | );
                   }
                   else if(w <= mid) {
                           Query_Min ( q , w , i << );
                   }
                   else {
                           Query_Min ( q , w , i << ) ;
                           Query_Min ( q , w , i <<  | );
                   }
          }
 }

 int LCA ( int x , int y ) {
          int px = fst[ x ] , py = fst[ y ] , tmp ;
          min_val = INF ;//初始化
          if ( py < px ) swap ( px , py ) ;
          Query_Min ( px , py ,  ) ;
          return ver[ min_pos ] ;//最小值在欧拉序中对应节点即为LCA
 }
 int main ( ) {
          int N ,M ;
          scanf ("%d",&N);
          for ( int i= ; i<=N- ; ++i ) {
                   int _x , _y , __ ;
                   scanf("%d %d %d" , &_x , &_y ,&__ ) ;
                   Add_Edge ( _x , _y , __ ) ;
                   Add_Edge ( _y , _x , __ ) ;
          }
          DFS (  ,  ) ;
          Build_Tree (  , dfs_num ,  ) ;
          DEBUG_( dfs_num ) ;
          scanf ("%d",&M);
          for ( int i= ; i<=M ; ++i ) {
                   int u , v ;
                   scanf ( "%d%d" , &u , &v ) ;
                   printf ("%d",LCA ( u , v ) ) ;
                   putchar('\n');
          }
          return  ;
 }

LCA->RMQ

————————————————分割线————————————————

　　方法二：

　　　　　倍增算法求LCA.

　　　　　 倍增算法的核心在于father[][]数组，father[ i ] [ j ] 表示从节点 i 开始，向上第2^j个节点编号。

　　　　　 可以通过以下的式子推出

father[ x ][ i ] = father[ father[ x ][ i - 1 ] ][ i - 1 ] ;

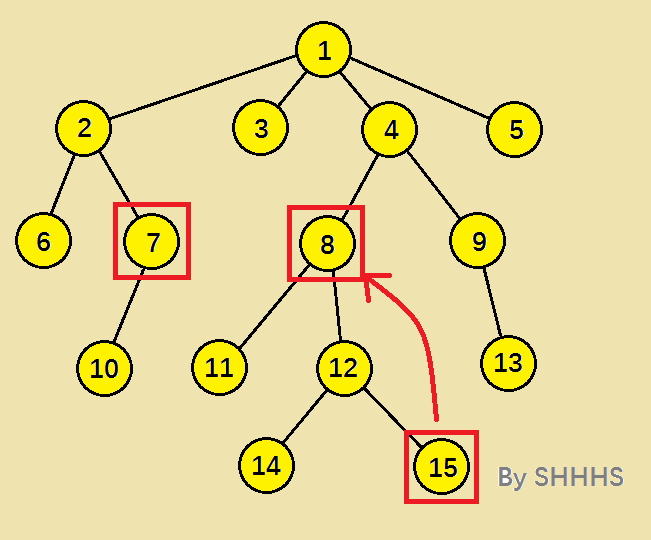
　　　　　 如下图，求节点 7 与 节点 15 的LCA 。

 首先找到深度较深的节点15 ， 让该节点向上移动，因为LCA一定在两节点的路径上。通过倍增思想，让该节点向上移动，使两个节点的深度相同。

if ( dep[ x ] < dep[ y ] )gswap( x , y ) ;
int t = dep[ x ] - dep[ y ] ;
for ( int i= ; i<= ; ++i )
          if( (  << i ) & t )
            x = father[ x ][ i ] ;

这时，两个节点深度相同，仍然通过倍增思想，让两节点以相同的速率向上跳，跳到两个节点的父节点恰好相等。

if( x == y ) return x ;//蜜汁特判
for ( int i= ; i>= ; --i ) {
          if ( father[ x ][ i ] == father[ y ][ i ] ) continue ;//跳多了，换一个小一点的值
          x = father[ x ][ i ] ;//两个节点以相同速率向上跳
          y = father[ y ][ i ] ;//
}

这时，两个节点的父节点就是LCA，直接返回父节点即可，算法结束。

[ATTENTION] : 这里需要加一个特判，如果两个节点调到同一位置直接返回。

核心代码&注释：

 inline void gswap ( int &x , int &y ) { int temp = x ; x = y ; y = temp ; }

 int cnt ;

 void Add_Edge ( const int x , const int y , const int val ) {//建边
         e[ ++cnt ].to = y ;
         e[ cnt ].val = val ;
         e[ cnt ].next = head[ x ] ;
         head[ x ] = cnt ;
 } 

 void DFS ( int x ) {
         vis[ x ] = true ;
         for ( int i= ; i<= ; ++i ) {
                 if ( dep[ x ] < (  << i ) ) break ;
                 father[ x ][ i ] = father[ father[ x ][ i -  ] ][ i -  ] ;//father数组的递推
         }
         for ( int i=head[ x ] ; i ; i=e[ i ].next ) {//图的DFS
                 int temp = e[ i ].to ;
                 if ( vis[ temp ] )continue ;
                 else {
                         Dis [ temp ] = Dis [ x ] + e[ i ].val ;
                         father[ temp ][  ] = x ;
                         dep[ temp ] = dep[ x ] +  ;
                         DFS ( temp ) ;
                 }
         }
 }
 int LCA ( int x , int y ) {
         if ( dep[ x ] < dep[ y ] )gswap( x , y ) ;
         int t = dep[ x ] - dep[ y ] ;//深度差
         for ( int i= ; i<= ; ++i ) if( (  << i ) & t ) x = father[ x ][ i ] ;//让深度较大的节点跳至深度相等
         if( x == y ) return x ;//蜜汁特判
         for ( int i= ; i>= ; --i ) {//两个节点同速率向上跳 到父亲恰好相等
                 if ( father[ x ][ i ] == father[ y ][ i ] ) continue ;
                 x = father[ x ][ i ] ; y = father[ y ][ i ] ;
         }
         return father[ x ][  ] ;// 返回父节点
 }

 int main ( ) {
         int N , Q ;
         scanf ( "%d" , &N ) ;
         for ( int i= ; i<=N- ; ++i ) {//读入建边
                 int _x , _y , _val ;
                 scanf ( "%d%d%d" , &_x , &_y , &_val ) ;
                 Add_Edge ( _x , _y , _val ) ;
                 Add_Edge ( _y , _x , _val ) ;
         }
         dep[  ] =  ;//
         DFS (  ) ;//以1为根节点DFS
         scanf ( "%d" , &Q ) ;
         while ( Q-- ) {
                 int _x , _y ;
                 scanf ( "%d%d" , &_x , &_y ) ;
                 printf ( "%d\n" ,LCA ( _x , _y ) ) ;
         }
 } 

倍增

—————————————分割线—————————————

方法二：

　　　　树的路径剖分算法求LCA。

　　　　(不懂树链剖分点这，树链剖分——精讲)

　　　　

　　　　对于一棵树，我们将其剖分为若干条链，记录每个节点所在链的链头，该节点的父节点。

　　　　当查询两节点LCA时

　　　　伪代码：

　　　　while ( x 与 y 不在同一条链上 )

　　　　　　　　if ( x的DFS序 > y的DFS序 )x = pre [ start[ x ] ] //通过链头跳到另一条链上

　　　　　　　　else if ( x的DFS序 < y的DFS序 )y = pre [ start[ y ] ]

　　　　if ( x的DFS序 > y的DFS序 ) print  ( y )

　　　　if ( x的DFS序 < y的DFS序 ) print  ( x )

算法图示：

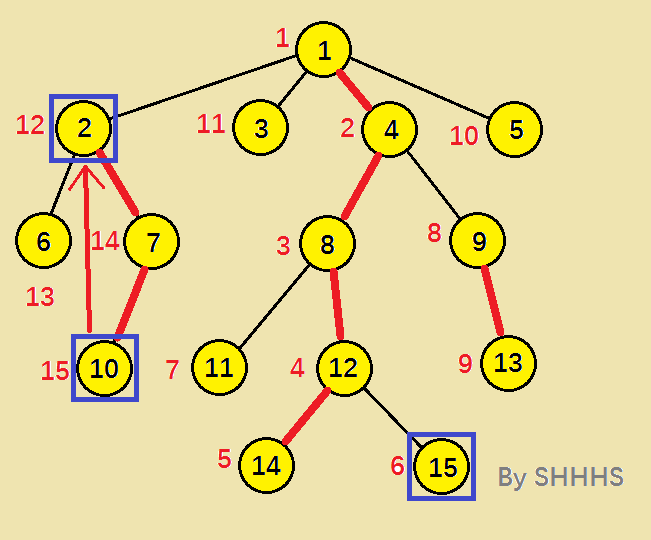
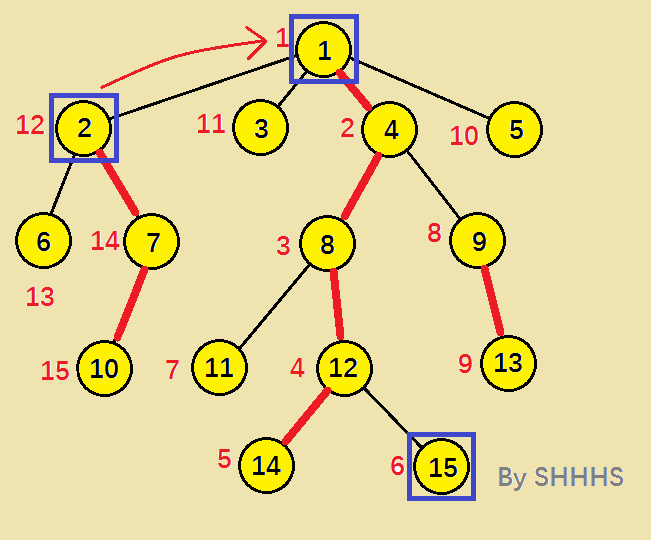
动态图：

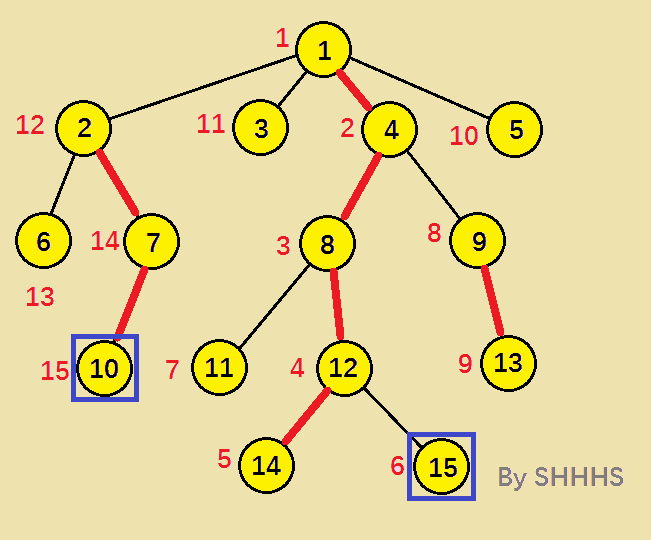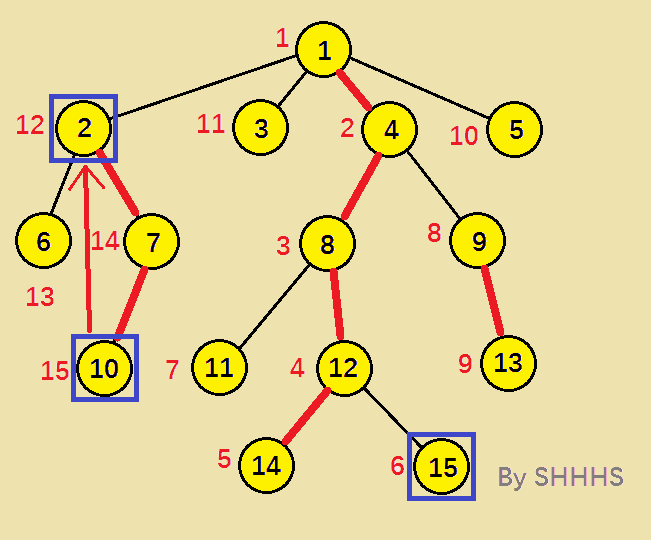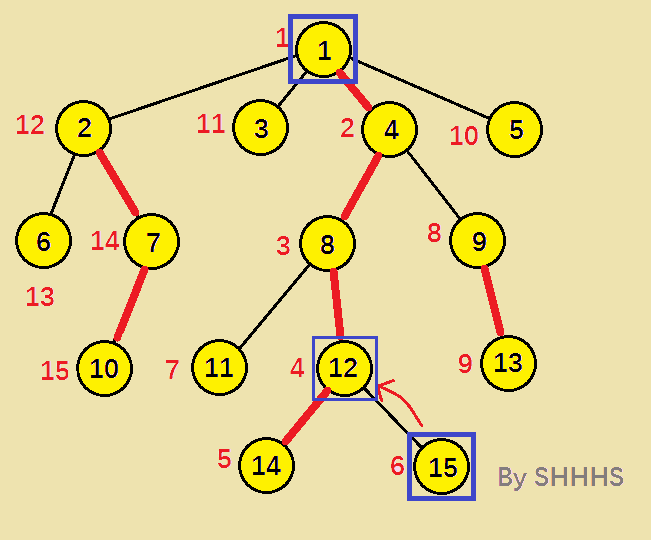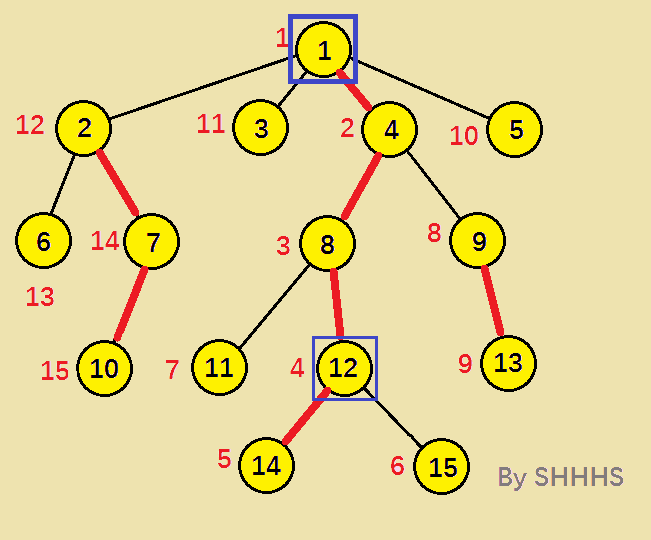
　　　　至此，两个节点在同一条链上，算法结束，DFS序较小的节点 1 即为LCA 。

 算法模板&注释：

 void Add_Edge ( const int _x , const int _y , const int _val ) {
          e[ ++cnt ].to = _y ;
          e[ cnt ].val = _val ;
          e[ cnt ].next = head[ _x ] ;
          head[ _x ] = cnt ;
 }

 int Init_DFS ( const int x , const int father ) {
          int cnt_ , max_ =  ;
          for ( int i=head[ x ] ; i ; i=e[ i ].next ) {
                   int temp = e[ i ].to ;
                   if ( temp==father ) continue ;
                   Dis[ temp ] = Dis[ x ] + e[ i ] .val ;
                   int _ = Init_DFS ( temp , x ) ;
                  if ( _ > max_ ) {max_ = _ ; hv[ x ] = temp ;}
                  cnt_ +=_;
          }
          return cnt_ ;
 }

 void DFS ( const int x , const int father ) {
          if ( !start[ x ] ) start[ x ] = start[ father ] ;
          DFN[ x ] = ++dfs_num ;
          if ( hv[ x ] ) DFS ( hv[ x ] , x ) ;
          for ( int i=head[ x ] ; i ; i =e[ i ].next ) {
                   if ( e[ i ].to != hv[ x ] && e[i].to != father ) {
                            int temp = e[ i ].to ;
                            start[ temp ] = temp ;
                            pre [ temp ] = x ;
                            DFS ( temp , x ) ;
                   }
          }
 }

 int LCA ( const int x , const int y ) {//start[]数组表示该点所在链的链头
          int px = x , py = y ;
          while ( start[ px ] != start[ py ] ) {//不在一条链上
                   if ( DFN[start[px]]>DFN[start[py] ] ) {//DFS序较大的跳
                            px = pre[ start[px] ] ;
                   }
                   else {
                            py = pre[ start[py] ] ;
                   }
          }
          return DFN[ px ] > DFN[ py ] ? py : px ;//返回DFS序较小的节点即为LCA
 }

树链剖分

———————————————分割线———————————————

方法四：

　　　　Tarjan算法求LCA.

　　　　[ATTENTION]:LCA的Tarjan算法与强连通分量的Tarjan算法无关。

2016-10-06 23:01:23

(完)