排序算法(sorting)

学习到的排序算法的总结，包括对COMP20003中排序部分进行总结，部分图片来自COMP20003

有部分内容来自http://www.cnblogs.com/eniac12/p/5329396.html

演示动画：https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html

---

概念：

stable sort: 相同的值排序后相对顺序不变。

Comparison-based sorting is Ω(nlogn).

---

Hash function ---

用数对list中的元素求余，根据余值放入对应的桶(bucket)中，使用素数(prime)能使得分配更为均匀。

Collisions冲突：两个元素的余值相同时发生。当buckets数量<元素数量，则一定发生。1个好的hash function应尽量少出现collison，但不能认为collision不会发生，换言之要做好应对。

Collision Resolution Methods

　　1.Chaining

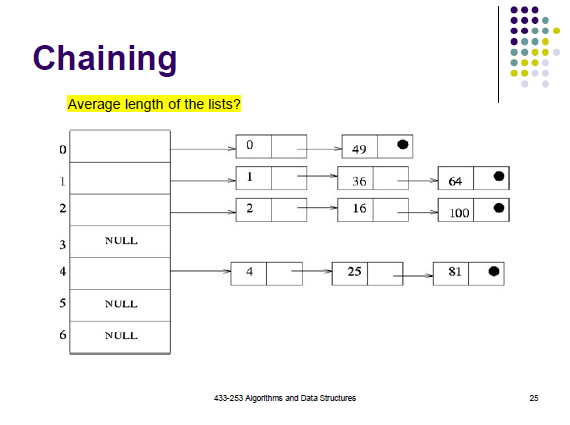
最坏情况：所有值都在同一bucket，实际上为linked list。

2.Open addressing methods

• • Linear probing

当插入位置已有数据时，插入下一空余位置（循环），若全满了，则collision。

• • Double hashing

当插入位置已有数据时，进行第二次求余得出新的位置。注意第二次求余值要+1避免在仍在原地。

---

Distribution counting --- unusual approach to sorting

　　计数排序(Counting sort):

requires: Key values to be within a certain range, lower to upper. 要排序的值在一定范围内。

通过记录所有数中，比该数小的有几个，来安排其位置。可以用辅助数组(auxiliary array)记录范围内比该值小(大)的有几个，也可以用for循环。用于整数排序。

 #include <stdio.h>
 #include <stdlib.h>

 int *countSort(int *n, int size);
 int *countSortIterative(int *n, int size);
 void printArray(int *n, int size);
 int min(int *n, int size);
 int max(int *n, int size);

 int main(int argc, char **argv) {
     int size = ;
     int unsortedArray[] = {,,,,,,,,,,,,,,,};
     int *sortedArray = NULL;
     printArray(unsortedArray, size);
     //sortedArray = countSort(unsortedArray, size);
     sortedArray = countSortIterative(unsortedArray, size);
     printArray(sortedArray, size);
     free(sortedArray);
     return ;
 } 

 void printArray(int *n, int size) {
     int i = ;
     for (i = ; i < size; i++) {
         printf("%d  ", n[i]);
     }
     printf("\n");
 }

 int *countSortIterative(int *n, int size) {
     int i = , j = ;
     int *sortedArray = NULL;
     int count = ;

     if((sortedArray = (int *) calloc(size, sizeof(int))) == NULL) {
         printf("calloc error\n");
         exit(EXIT_FAILURE);
     }

     for (i = ; i < size; i++) {
         for (j = , count = ; j < size; j++) {
             if (i == j) {
                 continue;
             }
             if (n[i] > n[j]) {
                 count++;
             }
             if (i > j && n[i] == n[j]) {
                 count++;
             }
         }
         sortedArray[count] = n[i];
     }
     return sortedArray;
 }

 int *countSort(int *n, int size) {
     int rangeFrom, rangeTo;
     int *cumulativeRecord = NULL;
     int *sortedArray = NULL;
     int i = ;

     rangeFrom = min(n, size);
     rangeTo = max(n, size);
     printf("size is %d, min is %d, max is %d\n", size, rangeFrom, rangeTo);

     if((cumulativeRecord = (int *) calloc(rangeTo - rangeFrom + , sizeof(int))) == NULL) {
         printf("calloc error\n");
         exit(EXIT_FAILURE);
     }
     for (i = ; i < size; i++) {
         cumulativeRecord[n[i] - rangeFrom]++;
     }
     for(i = ; i < rangeTo - rangeFrom + ; i++) {
         if (i == ) {
             continue;
         }
         cumulativeRecord[i] = cumulativeRecord[i] + cumulativeRecord[i - ];
     }
     //printArray(cumulativeRecord, rangeTo - rangeFrom + 1);
     if((sortedArray = (int *)malloc(size * sizeof(int))) == NULL) {
         printf("malloc error\n");
         exit(EXIT_FAILURE);
     } 

     for ( i = ; i < size; i++) {
         sortedArray[cumulativeRecord[n[i] - rangeFrom]-] = n[i];
         cumulativeRecord[n[i] - rangeFrom] --;
     }
     //printArray(sortedArray, size);
     free(cumulativeRecord);
     return sortedArray;
 }

 int min(int *n, int size) {
     int i = ;
     int min = n[];
     for (i = ; i < size; i++) {
         if (min > n[i]) {
             min = n[i];
         }
     }
     return min;
 }
 int max(int *n, int size) {
     int i = ;
     int max = n[];
     for (i = ; i < size; i++) {
         if (max < n[i]) {
             max = n[i];
         }
     }
     return max;
 }

复杂度：O(n)   (non-comparison-based)

---

冒泡排序Bubble sort

使用双循环逐个对相邻元素进行比较，将较大（小）的元素放在后面，经过一次循环，最大（小）的元素被排到末尾。该方法就如名字一般，将较大（小）的浮上来。

worst case: O(n^2)
best case: O(n) 如果设一flag变量检测有无进行元素交换，则在已按顺序排好的list中，第一次循环时，没有进行交换而停止。
average case: O(n^2)
stable sort

 /* sort the array from min to max
     worst case: O(n^2)
     best case: O(n) if set a flag to detect whether swap the elements
     average case: O(n^2)
     stable sort
 */

 #include <stdio.h>

 void swap(int *array, int a, int b) {
     int temp = array[a];
     array[a] = array[b];
     array[b] = temp;
 }

 void bubbleSort(int *array, int size) {
     int i, range, swapFlag = ;

     for (range = size - ; range > ; range--) {
         for (i = ; i < range; i++) {
             if (array[i] > array[i + ]) {
                 swap(array, i, i + );
                 swapFlag = ;
             }
         }
         if (swapFlag == ) {
             break;
         }
     }
 }

 int main(int argc, char **argv) {
     int array[] = {, -, , , , };
     int i;
     bubbleSort(array, );
     for (i = ; i < ; i++) {
         printf("%d  ", array[i]);
     }
     printf("\n");
     return ;
 }

---

选择排序Selection sort

选择排序是一种简单直观的排序算法。它的工作原理很容易理解：初始时在序列中找到最小（大）元素，放到序列的起始位置作为已排序序列；然后，再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

　　注意选择排序与冒泡排序的区别：冒泡排序通过依次交换相邻两个顺序不合法的元素位置，从而将当前最小（大）元素放到合适的位置；而选择排序每遍历一次都记住了当前最小（大）元素的位置，最后仅需一次交换操作即可将其放到合适的位置。

worst case: O(n^2)
best case: O(n^2)
average case: O(n^2)
unstable sort:

　　选择排序是不稳定的排序算法，不稳定发生在最小元素与A[i]交换的时刻。

　　比如序列：{ 5, 8, 5, 2, 9 }，一次选择的最小元素是2，然后把2和第一个5进行交换，从而改变了两个元素5的相对次序。

 #include <stdio.h>

 /* sort the array from min to max
     worst case: O(n^2)
     best case: O(n^2)
     average case: O(n^2)
     unstable sort
 */
 void selectionSort(int *array, int size);
 void swap(int *array, int a, int b);
 void printArray(int *n, int size);

 int main(int argc, char **argv) {
     int array[] = {,,,,,,,,,};
     printArray(array, );
     selectionSort(array, );
     printArray(array, );
     return ;
 }

 /* sort the array from min to max */
 void selectionSort(int *array, int size) {
     int i, j, min;

     for (i = ; i < size - ; i++) {
         min = i;
         for (j = i + ; j < size; j++) {
             if (array[min] > array[j]) {
                 min = j;
             }
         }
         if (i != min) {
             swap(array, i, min);
         }
     }
 }

 void swap(int *array, int a, int b) {
     int temp = array[a];
     array[a] = array[b];
     array[b] = temp;
 }

 void printArray(int *n, int size) {
     int i = ;
     for (i = ; i < size; i++) {
         printf("%d  ", n[i]);
     }
     printf("\n");
 }

---

插入排序Insertion sort

　　类似于打扑克时抽牌时的操作，抽到第n张时，与前一张比较大小，直到前一张的牌比第n张小，则插入此位置。

worst case O(n^2)
average case O(n^2)
best case O(n): 当list已经拍好顺序时。
stable sort

 #include <stdio.h>
 /* sort the array from min to max
     worst case O(n^2)
     average case O(n^2)
     best case O(n)
     stable sort
 */
 void insertionSort(int *array, int size);
 void printArray(int *n, int size);

 int main(int argc, char **argv) {
     int array[] = {-, , , , -, , , , , };
     printArray(array, );
     insertionSort(array, );
     printArray(array, );
     return ;
 }

 void insertionSort(int *array, int size) {
     int i = , j, insertionVal;
     for (i = ; i < size; i++) {
         insertionVal = array[i];
         j = i;
         while( j -  >=  && array[j - ] > insertionVal) {
             array[j] = array[j - ];
             j--;
         }
         array[j] = insertionVal;
     }
 }

 void printArray(int *n, int size) {
     int i = ;
     for (i = ; i < size; i++) {
         printf("%d  ", n[i]);
     }
     printf("\n");
 }

---

分治策略(divide-and-conquer sorting algorithm)：

快速排序(Quicksort)---Hard split, easy join：

　　Partition array:

Pick Pivot, which it is in its final position

Everything larger than pivot has higher index

Everything less than pivot has lower index

选择一个pivot枢纽(？不知道中文该对应哪个)，可以是最左边或最右边等由自己决定，根据pivot的选择不同，会有不同效果。比pivot大的排在pivot右边，小的排在左边，只是如此，在左边的和右边的序列并未按序。

Recursion:

Partition left-half(recursively)

Partition right-half(recursively)

Base case:singletons are already sorted

如此不断递归。

注意：在选择pivot时，最后将pivot放置到正确位置，如选择最左作为pivot，在partition时，最后将从右开始筛选的替换。

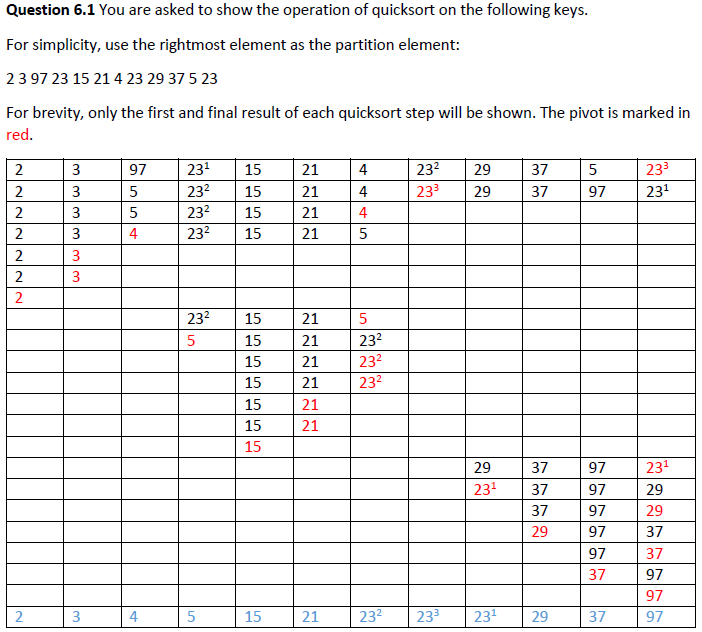
 #include <stdio.h>
 #include <stdlib.h>

 void quicksort(int *n, int l, int r);
 void printArray(int *n, int i);
 int partition(int *n, int l, int r);
 int partitionLeft(int *n, int l, int r);
 int partitionRight(int *n, int l, int r);
 void swap(int *n, int i, int j);

 int main(int argc, char **argv) {
     int *n = (int *) malloc(sizeof(int));
     int i = ;
     int data;
     while (scanf("%d", &data) == ) {
         n = realloc(n, sizeof(int) * (i + ));
         n[i] = data;
         i++;
     }
     printArray(n, i);
     quicksort(n, , i - );

     printArray(n, i);
     free(n);
     return ;
 }

 void printArray(int *n, int i) {
     int j = ;
     for (j = ; j < i; j++) {
         printf("%d   ", n[j]);
     }
     printf("\n");
 }

 void quicksort(int *n, int l, int r) {
     int i;
     if (l >= r) {
         return;
     }
     i = partition(n, l, r);
     quicksort(n, l, i - );
     quicksort(n, i + , r);
 }

 int partition(int *n, int l, int r) {
     return partitionLeft(n, l, r);
     //return partitionRight(n, l, r);
 }

 int partitionLeft(int *n, int l, int r) {
     int pivot = n[l];
     int left = l;
     int right = r + ;
     while() {
         do{
             left++;
         } while(n[left] < pivot);
         do{
             right--;
         } while(n[right] > pivot);

         if (left >= right) {
             break;
         }
         swap(n, left, right);
     }
     swap(n, l, right);
     return right;
 }

 int partitionRight(int *n, int l, int r) {
     int pivot = n[r];
     int left = l - ;
     int right = r;
     while() {
         do{
             left++;
         } while(n[left] < pivot);
         do{
             right--;
         } while(n[right] > pivot);

         if (left >= right) {
             break;
         }
         swap(n, left, right);
     }
     swap(n, r, left);
     return left;
 }

 void swap(int *n, int i, int j) {
     int temp = n[i];
     n[i] = n[j];
     n[j] = temp;
 }

归并排序(Mergesort)---Easy split, hard join：

关键：当有两个已排好顺序的list（array or linked list）要合并(merge)成一个时，使用两个指针分别指向两个lists，比较其大小，小的放入新list，其对应指针指向下一个，直到两个lists都装入新list。

 /* merge two sorted arrays, first -- mid, mid + 1 -- last  */
 void merge(int *array, int first, int mid, int last) {
     int newArray[last - first + ];
     int i, j, k;
     for (i = first, j = mid + , k = ; k < last - first + ; k++) {
         if (i > mid) {
             newArray[k] = array[j++];
             continue;
         }
         if (j > last) {
             newArray[k] = array[i++];
             continue;
         }
         if (array[i] < array[j]) {
             newArray[k] = array[i++];
         } else {
             newArray[k] = array[j++];
         }
     }

     /* paste newArray to array */
     for (i = first, k = ; i <= last ; i++, k++) {
         array[i] = newArray[k];
     }
 }

分为两种：1.Top-down mergesort(recursive)

将list不断一分为二，直到分成单个为止，然后开始合并，使用递归。

 void mergeSortRecursion(int *array, int first, int last) {
     int mid = (first + last) / ;

     if (first == last) {
         return;
     }
     mergeSortRecursion(array, first, mid);
     mergeSortRecursion(array, mid + , last);
     merge(array, first, mid, last);
 }

　　　　　2.Bottom-up mergesort(iterative)

将list看作是由单个元素的lists组成的，两两合并，使用迭代。

 void mergeSortIterative(int *array, int len) {
     int i, first, mid, last;
     for (i = ; i < len; i *= ) {
         first = ;
         while(first + i < len) {
             mid = first + i - ;
             last = mid + i < len ? mid + i : len - ;
             merge(array, first, mid, last);
             printf("first = %d, mid = %d, last = %d\n", first, mid, last);
             first = last + ;
         }
         printArray(array, len);
     }
 }

使用链表完成的bottom-up mergesort(iterative)放在了我的github：https://github.com/Will-Zhu-27/Algorithms-and-Data-Structures/tree/master/sorting/merge%20sort%20in%20linked%20list