主成分分析 SPSS、python实例分析

更新：

　　这次决定用matlab手把手一步一步实现一遍。

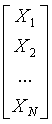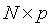令是一个的观测矩阵，观测向量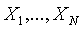的样本均值M，由下式给出：

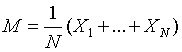
　　Matlab中我们给出矩阵.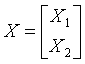

　　　　 　　

　　用a，b度量矩阵X的行列数并分别计算每一列计算M的值

　　　　 

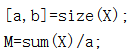
　　样本均值是散列图的中心，对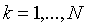，令

　　 

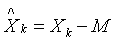
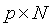矩阵的列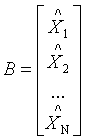

具有零样本均值，这样的B称为平均偏差形式。

　　　　 

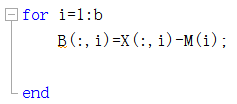
主成分分析的目标是找到一个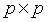正交矩阵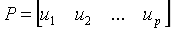,确定一个变量代换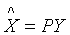,或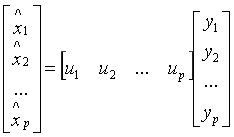并具有新的变量y₁,...,y_p两两无关的性质，且整理后的方差具有递减顺序。

变量的正交变换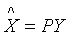说明，每一个观测向量X_k得到一个“新名称”Y_k，使得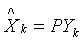，注意到Y_k是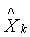相对于以P的列为基的坐标向量。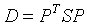为对角形，P记为正交矩阵，它的列是单位特征向量，那么.

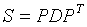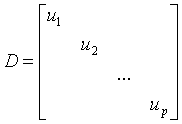
（样本）协方差矩阵是一个矩阵S，其定义为：

　　 

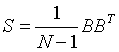
由于任何具有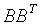形式的矩阵是半正定的，所以S也是半正定的。

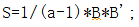
数据的总方差是指S中对角线上方差的综合。一般地，一个方阵S中对角元素之和称为矩阵的迹，记作tr(S),这样

{总方差}=tr{S}

S中的元素称为x_i和x_j的协方差。 　　

　　　　

将特征值从大到小排序，取贡献率到90%的前k个特征。

　　　　

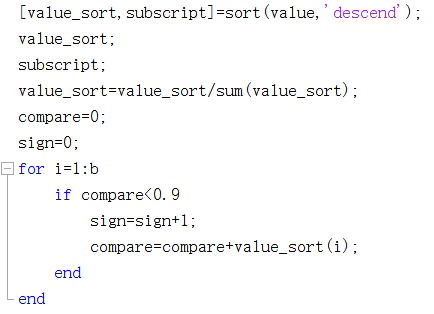
可得到P、D

　　　　

下面贴完整代码:

clc;
clear all;
close all;

X=[2.5 2.4;
   0.5 0.7;
   2.2 2.9;
   1.9 2.2;
   3.1 3.0;
   2.3 2.7;
   2 1.6;
   1 1.1;
   1.5 1.6;
   1.1 0.9;];
X=X'

% X=[74 87 84 88 74 86 69 73 64;
%    85 83 83 77 69 84 74 85 84;
%    83 91 89 85 87 86 83 86 85;
%    69 100 82 96 84 82 97 98 76;
%    97 48 89 36 46 53 88 89 97;
%    59 98 93 94 98 100 79 83 61;];
% X=X';

% X=[2 0 -1.4;
%    2.2 0.2 -1.5;
%    2.4 0.1 -1;
%    1.9 0 -1.2;];
% X=X';
[a,b]=size(X);
M=sum(X)/a;

for i=1:b
    B(:,i)=X(:,i)-M(i);
    %B=zscore(X);
end

S=1/(a-1)*B*B';
[vector,value]=eig(S);
vector
value=diag(value)
varine=sum(value);

[value_sort,subscript]=sort(value,'descend');
value_sort;
subscript;
value_sort=value_sort/sum(value_sort);
compare=0;
sign=0;
for i=1:b
    if compare<0.9
        sign=sign+1;
        compare=compare+value_sort(i);
    end
end

for i=1:sign
    P(:,i)=vector(:,subscript(i));
end
P

D=zeros(sign,sign);
for i=1:sign
    D(i,i)=value(subscript(i));
end
D

　　

---

　　主成分分析（Principal Component Analysis，PCA）， 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。

　　主成分分析，是考察多个变量间相关性一种多元统计方法，研究如何通过少数几个主成分来揭示多个变量间的内部结构，即从原始变量中导出少数几个主成分，使它们尽可能多地保留原始变量的信息，且彼此间互不相关.通常数学上的处理就是将原来P个指标作线性组合，作为新的综合指标。

　　简单说，主成分分析的作用是降维。通过降维将原来多变量解释的问题，映射到更少指标，转换成少变量的可解释性问题。但是注意经过主成分分析后的变量与原变量不存在逻辑关系，仅仅是存在线性组合的关系。[1]

。

 一、算法原理：

---

输入：样本集D={x₁,x_2...x_m}；

　　　低维空间维数d'.

过程：

1.对所有样本进行中心化：

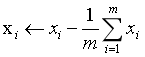
2.计算样本的协方差矩阵XX^T；

3.对协方差矩阵XX^T做特征值分解；

4.取最大的d'个特征值所对应的特征向量w₁，w₂...w_d';

输出：投影矩阵W*=（w₁，w₂...w_d'） .[2]

---

二、PCA原理

　　

　　

　　

三、SPSS进行主成分分析

　　由于SPSS本身就是一个用于数据分析的软件，因此操作简单无需编程，即可直观感受主成分分析带来的效果。

　　先胡乱编制了一些数据：

　　

　　

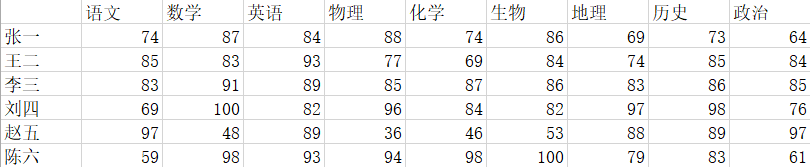
　　在SPSS里，点击分析->降维->因子，在弹出的对话框中，将需要分析的变量都送入变量栏中。根据个人需要在描述、提取、旋转、得分、选项中勾选。此处我们注意在提取中勾选主成分。

　　

点击“确定”：

　　

　　

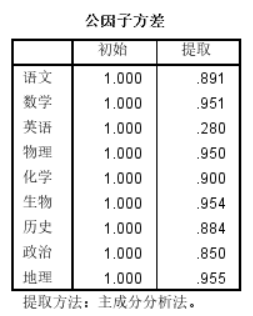
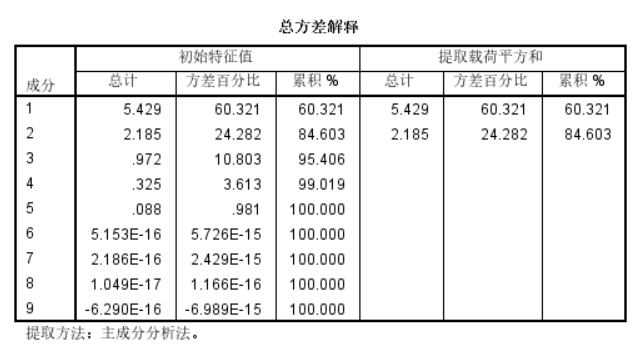
最后我们可以看到提取了两个主成分

　　

　　

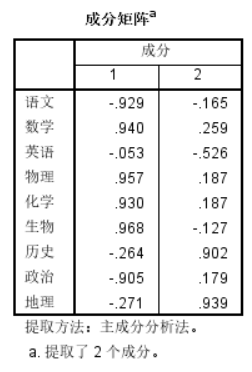
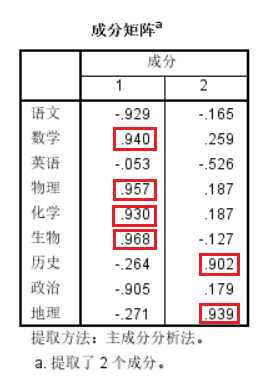
观察两个主成分中的贡献率，我们会发现第一个主成分包含贡献率较高的项为数学、物理、化学、生物，实际意义即理科，第二主成分包含历史、地理，即文科。具有良好解释性。

四、python代码实现主成分分析

pca.py

# -*- coding: utf-8 -*-
"""
Created on Sun Feb 28 10:04:26 2016
PCA source code
@author: liudiwei
"""

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#计算均值,要求输入数据为numpy的矩阵格式，行表示样本数，列表示特征
def meanX(dataX):
    return np.mean(dataX,axis=0)#axis=0表示按照列来求均值，如果输入list,则axis=1

#计算方差,传入的是一个numpy的矩阵格式，行表示样本数，列表示特征
def variance(X):
    m, n = np.shape(X)
    mu = meanX(X)
    muAll = np.tile(mu, (m, 1))
    X1 = X - muAll
    variance = 1./m * np.diag(X1.T * X1)
    return variance

#标准化,传入的是一个numpy的矩阵格式，行表示样本数，列表示特征
def normalize(X):
    m, n = np.shape(X)
    mu = meanX(X)
    muAll = np.tile(mu, (m, 1))
    X1 = X - muAll
    X2 = np.tile(np.diag(X.T * X), (m, 1))
    XNorm = X1/X2
    return XNorm

"""
参数：
	- XMat：传入的是一个numpy的矩阵格式，行表示样本数，列表示特征
	- k：表示取前k个特征值对应的特征向量
返回值：
	- finalData：参数一指的是返回的低维矩阵，对应于输入参数二
	- reconData：参数二对应的是移动坐标轴后的矩阵
"""
def pca(XMat, k):
    average = meanX(XMat)
    m, n = np.shape(XMat)
    data_adjust = []
    avgs = np.tile(average, (m, 1))
    data_adjust = XMat - avgs
    covX = np.cov(data_adjust.T)   #计算协方差矩阵
    featValue, featVec=  np.linalg.eig(covX)  #求解协方差矩阵的特征值和特征向量
    index = np.argsort(-featValue) #按照featValue进行从大到小排序
    finalData = []
    if k > n:
        print("k must lower than feature number")
        return
    else:
        #注意特征向量时列向量，而numpy的二维矩阵(数组)a[m][n]中，a[1]表示第1行值
        selectVec = np.matrix(featVec.T[index[:k]]) #所以这里需要进行转置
        finalData = data_adjust * selectVec.T
        reconData = (finalData * selectVec) + average
    return finalData, reconData

def loaddata(datafile):
    return np.array(pd.read_csv(datafile,sep="\t",header=-1)).astype(np.float)

def plotBestFit(data1, data2):
    dataArr1 = np.array(data1)
    dataArr2 = np.array(data2)

    m = np.shape(dataArr1)[0]
    axis_x1 = []
    axis_y1 = []
    axis_x2 = []
    axis_y2 = []
    for i in range(m):
        axis_x1.append(dataArr1[i,0])
        axis_y1.append(dataArr1[i,1])
        axis_x2.append(dataArr2[i,0])
        axis_y2.append(dataArr2[i,1])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(axis_x1, axis_y1, s=50, c='red', marker='s')
    ax.scatter(axis_x2, axis_y2, s=50, c='blue')
    plt.xlabel('x1'); plt.ylabel('x2');
    plt.savefig("outfile.png")
    plt.show()	

#简单测试
#数据来源：http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html
def test():
    X = [[2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1],
         [2.4, 0.7, 2.9, 2.2, 3.0, 2.7, 1.6, 1.1, 1.6, 0.9]]
    XMat = np.matrix(X).T
    k = 2
    return pca(XMat, k)

#根据数据集data.txt
def main():
    datafile = "data.txt"
    XMat = loaddata(datafile)
    k = 2
    return pca(XMat, k)

if __name__ == "__main__":
    finalData, reconMat = main()
    plotBestFit(finalData, reconMat)

data.txt

5.1	3.5	1.4	0.2
4.9	3.0	1.4	0.2
4.7	3.2	1.3	0.2
4.6	3.1	1.5	0.2
5.0	3.6	1.4	0.2
5.4	3.9	1.7	0.4
4.6	3.4	1.4	0.3
5.0	3.4	1.5	0.2
4.4	2.9	1.4	0.2
4.9	3.1	1.5	0.1
5.4	3.7	1.5	0.2
4.8	3.4	1.6	0.2
4.8	3.0	1.4	0.1
4.3	3.0	1.1	0.1
5.8	4.0	1.2	0.2
5.7	4.4	1.5	0.4
5.4	3.9	1.3	0.4
5.1	3.5	1.4	0.3
5.7	3.8	1.7	0.3
5.1	3.8	1.5	0.3
5.4	3.4	1.7	0.2
5.1	3.7	1.5	0.4
4.6	3.6	1.0	0.2
5.1	3.3	1.7	0.5
4.8	3.4	1.9	0.2
5.0	3.0	1.6	0.2
5.0	3.4	1.6	0.4
5.2	3.5	1.5	0.2
5.2	3.4	1.4	0.2
4.7	3.2	1.6	0.2
4.8	3.1	1.6	0.2
5.4	3.4	1.5	0.4
5.2	4.1	1.5	0.1
5.5	4.2	1.4	0.2
4.9	3.1	1.5	0.1
5.0	3.2	1.2	0.2
5.5	3.5	1.3	0.2
4.9	3.1	1.5	0.1
4.4	3.0	1.3	0.2
5.1	3.4	1.5	0.2
5.0	3.5	1.3	0.3
4.5	2.3	1.3	0.3
4.4	3.2	1.3	0.2
5.0	3.5	1.6	0.6
5.1	3.8	1.9	0.4
4.8	3.0	1.4	0.3
5.1	3.8	1.6	0.2
4.6	3.2	1.4	0.2
5.3	3.7	1.5	0.2
5.0	3.3	1.4	0.2
7.0	3.2	4.7	1.4
6.4	3.2	4.5	1.5
6.9	3.1	4.9	1.5
5.5	2.3	4.0	1.3
6.5	2.8	4.6	1.5
5.7	2.8	4.5	1.3
6.3	3.3	4.7	1.6
4.9	2.4	3.3	1.0
6.6	2.9	4.6	1.3
5.2	2.7	3.9	1.4
5.0	2.0	3.5	1.0
5.9	3.0	4.2	1.5
6.0	2.2	4.0	1.0
6.1	2.9	4.7	1.4
5.6	2.9	3.6	1.3
6.7	3.1	4.4	1.4
5.6	3.0	4.5	1.5
5.8	2.7	4.1	1.0
6.2	2.2	4.5	1.5
5.6	2.5	3.9	1.1
5.9	3.2	4.8	1.8
6.1	2.8	4.0	1.3
6.3	2.5	4.9	1.5
6.1	2.8	4.7	1.2
6.4	2.9	4.3	1.3
6.6	3.0	4.4	1.4
6.8	2.8	4.8	1.4
6.7	3.0	5.0	1.7
6.0	2.9	4.5	1.5
5.7	2.6	3.5	1.0
5.5	2.4	3.8	1.1
5.5	2.4	3.7	1.0
5.8	2.7	3.9	1.2
6.0	2.7	5.1	1.6
5.4	3.0	4.5	1.5
6.0	3.4	4.5	1.6
6.7	3.1	4.7	1.5
6.3	2.3	4.4	1.3
5.6	3.0	4.1	1.3
5.5	2.5	4.0	1.3
5.5	2.6	4.4	1.2
6.1	3.0	4.6	1.4
5.8	2.6	4.0	1.2
5.0	2.3	3.3	1.0
5.6	2.7	4.2	1.3
5.7	3.0	4.2	1.2
5.7	2.9	4.2	1.3
6.2	2.9	4.3	1.3
5.1	2.5	3.0	1.1
5.7	2.8	4.1	1.3
6.3	3.3	6.0	2.5
5.8	2.7	5.1	1.9
7.1	3.0	5.9	2.1
6.3	2.9	5.6	1.8
6.5	3.0	5.8	2.2
7.6	3.0	6.6	2.1
4.9	2.5	4.5	1.7
7.3	2.9	6.3	1.8
6.7	2.5	5.8	1.8
7.2	3.6	6.1	2.5
6.5	3.2	5.1	2.0
6.4	2.7	5.3	1.9
6.8	3.0	5.5	2.1
5.7	2.5	5.0	2.0
5.8	2.8	5.1	2.4
6.4	3.2	5.3	2.3
6.5	3.0	5.5	1.8
7.7	3.8	6.7	2.2
7.7	2.6	6.9	2.3
6.0	2.2	5.0	1.5
6.9	3.2	5.7	2.3
5.6	2.8	4.9	2.0
7.7	2.8	6.7	2.0
6.3	2.7	4.9	1.8
6.7	3.3	5.7	2.1
7.2	3.2	6.0	1.8
6.2	2.8	4.8	1.8
6.1	3.0	4.9	1.8
6.4	2.8	5.6	2.1
7.2	3.0	5.8	1.6
7.4	2.8	6.1	1.9
7.9	3.8	6.4	2.0
6.4	2.8	5.6	2.2
6.3	2.8	5.1	1.5
6.1	2.6	5.6	1.4
7.7	3.0	6.1	2.3
6.3	3.4	5.6	2.4
6.4	3.1	5.5	1.8
6.0	3.0	4.8	1.8
6.9	3.1	5.4	2.1
6.7	3.1	5.6	2.4
6.9	3.1	5.1	2.3
5.8	2.7	5.1	1.9
6.8	3.2	5.9	2.3
6.7	3.3	5.7	2.5
6.7	3.0	5.2	2.3
6.3	2.5	5.0	1.9
6.5	3.0	5.2	2.0
6.2	3.4	5.4	2.3
5.9	3.0	5.1	1.8

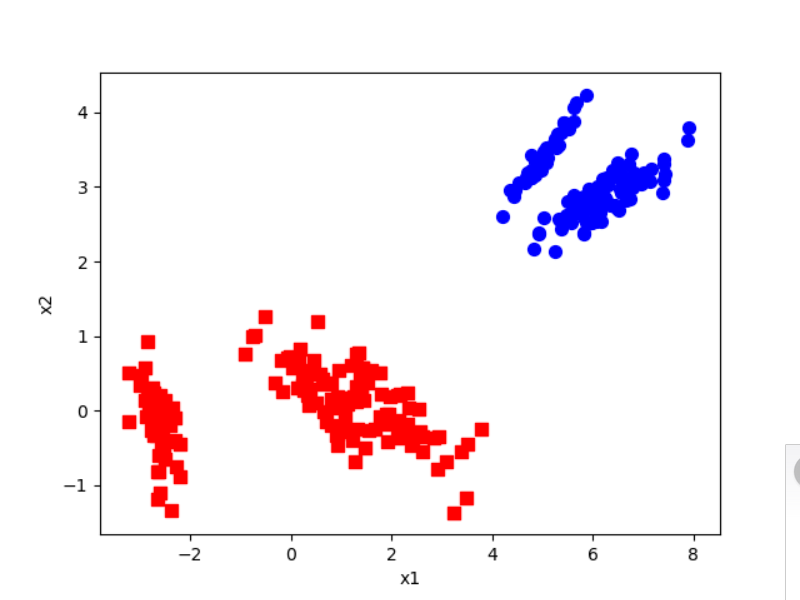
　　代码运行结果：

参考文献：

[1] https://baike.baidu.com/item/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90/829840?fr=aladdin

[2]周志华，机器学习，清华大学出版社，2016年1月1版.

2019-03-09

00:05:40