最小可用id

题目：在非负数组（乱序）中找到最小的可分配的id（从1开始编号），数据量10000000。

题目解读：在一个不重复的乱序的自然数组中找到最小的缺失的那个数，比如1，2，3，6，4，5，8，11。那么最小可用id就为7。

代码：

import java.util.Arrays;

/**
 * 解决最小可用id问题
 */
public class MinFreeId {

    public static void main(String[] args) {

//        int[]arr = {1,5,3,2,6,7,10,9,4};  // 最开始小数据测试
        int []arr = new int[1000*1000];
        for (int i = 0; i < arr.length; i++) {
            // if(i==900000) 那解法一运行时间就太长了
            if (i==90000) {
                arr[i] = arr.length+10;
            }else {
                arr[i] = i+1;
            }
        }
        long now = System.currentTimeMillis();
        System.out.println(find1(arr));
        System.out.println("解法一消耗的时间："+(System.currentTimeMillis()-now)+"ms");

        now = System.currentTimeMillis();
        System.out.println(find2(arr));
        System.out.println("解法二消耗的时间："+(System.currentTimeMillis()-now)+"ms");

        now = System.currentTimeMillis();
        System.out.println(find3(arr));
        System.out.println("解法三消耗的时间："+(System.currentTimeMillis()-now)+"ms");

        now = System.currentTimeMillis();
        System.out.println(find4(arr,0,arr.length-1));
        System.out.println("解法四消耗的时间："+(System.currentTimeMillis()-now)+"ms");

    }

    // O(n^2) 暴力解法：从1开始依次探测每个自然数是否在数组中
    static int find1(int[]arr){
        int i = 1;
        while(true){
            for (int j = 0; j < arr.length;) {
                if (arr[j]==i) {
                    i++;
                    j = 0;
                    continue;
                }else {
                    j++;
                }
            }
            return i;
        }
    }

    // O(nlgn)
    static int find2(int[]arr){
        Arrays.sort(arr);  // O(nlgn)  后续扫描时间O(N) 相比之下 取O(nlgn) 所以时间复杂度为O(nlgn)
        int i = 0;
        while(i<arr.length){
            if (i+1!=arr[i]) {  // 不存在的最小自然数
                return i+1;
            }
            i++;
        }
        return i+1;
    }

    /**
     * 改进1：用辅助空间
     * 有点类似计数排序  O(N)但是浪费空间
     */
    static int find3(int[]arr){
        int n = arr.length;
        int []helper = new int[n+1];
        for (int i = 0; i < n; i++) {  //   O(N)
            if (arr[i]<n+1) {
                helper[arr[i]] = 1;  // 辅助空间的下标也是有用的
            }
        }
        for (int i = 1; i <= n; i++) {  //   O(N)

            if (helper[i] == 0) {
                return i;
            }
        }
        return n+1;
    }

    /**
     * //   O(N)
     * 改进2：分区，递归
     * 问题可转化为：n的正数的数组A,如果存在小于n的数不在数组中，必然存在大于n的数组中，否则数组排列恰好为1到n
     */

    private static int find4(int[] arr, int l, int r) {
        if (l>r) {
            return l+1;
        }
        int midIndex = l+((r-l)>>1);  // 中间下标
        int q = SelectK.selectK(arr, l, r, midIndex-l+1);  // 调用查找第k大的元素的方法
        int t = midIndex + 1;  // 期望值
        if (q==t) {  // 左侧紧密
            return find4(arr,midIndex+1,r);
        }else {  // 左侧稀疏
            return find4(arr, l, midIndex-1);
        }
    }
}

结果：

　　

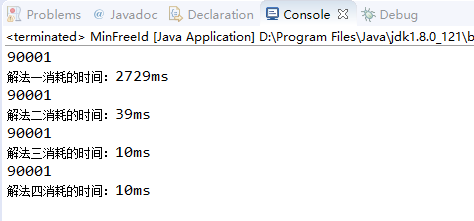
结论：根据每个解法所消耗的时间即可得出哪个解法的效率更高。所以在数据量较大的情况下最好选用O(lgn)和O(N)级别的算法，O(nlgn)次之。