Theano入门神经网络(二) 实现一个XOR门

与非门的图片如下

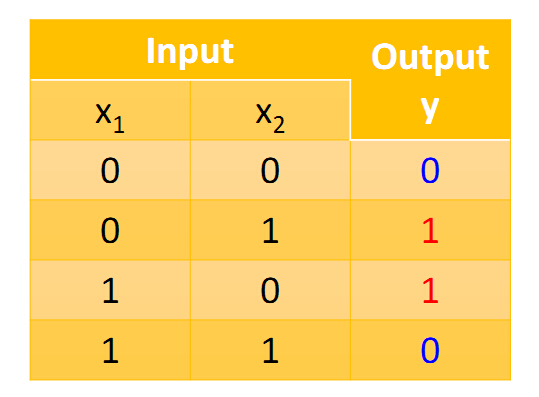
示意图

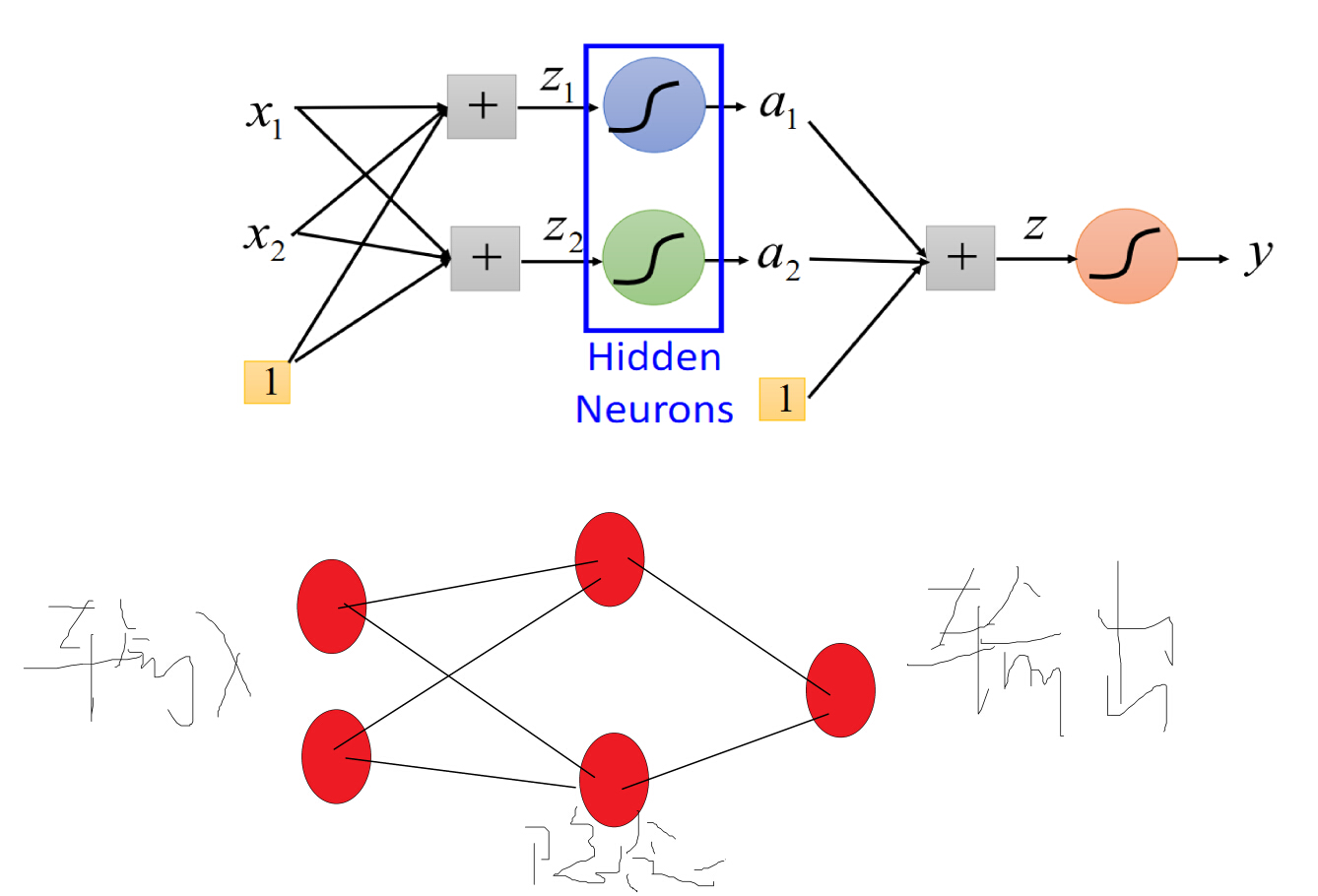
详细解释：

1 定义变量的代码，包括了输入、权值、输出等。其中激活函数采用的是sigmod函数

 # -*- coding: utf-8 -*-
 __author__ = 'Administrator'

 import theano
 import  theano.tensor as T
 import  random
 import  numpy as np
 from itertools import izip

 #定义网络结构
 #定义输入
 x=T.vector()
 #定义权值W1
 w1=theano.shared(np.random.randn(2)) #生成一个1行2列的随机数
 w2=theano.shared(np.random.randn(2))
 b1=theano.shared(np.random.randn(1))
 b2=theano.shared(np.random.randn(1))
 z1=T.dot(w1,x)+b1
 a1=1/(1+T.exp(-z1))
 z2=T.dot(w2,x)+b2
 a2=1/(1+T.exp(-z2))

 w=theano.shared(np.random.randn(2))
 b=theano.shared(np.random.randn(1))
 z=T.dot(w,[a1,a2])+b
 y=1/(1+T.exp(-z))

2 定义目标输出和损失函数计算方式，我们采用的平方损失

 y_hat = T.scalar()#正确输出
 cost = T.sum((y-y_hat)**2) #采用的是平方损失函数

另外也可以采用交叉熵损失函数

cost = - (y_hat*T.log(y)+(1-y_hat)*T.log(1-y)).sum() #采用交叉熵损失函数

3 误差反向传播求导，直接调用theano函数求解，方便快捷

 #误差反向传播求导
 dw,db,dw1,dw2,db1,db2= T.grad(cost,[w,b,w1,w2,b1,b2])

4 权值更新

 #手动定义一个权值更新函数
 def MyUpdate(paramters,gradients):
     mu=0.1 #步长
     paramters_updates= \
     [(p, p-mu*g) for p,g in izip(paramters,gradients)]
     return paramters_updates

 #绑定输入、输出与权值更新函数
 g = theano.function(
     inputs=[x,y_hat],
     outputs=[y,cost],
     updates=MyUpdate([w,b,w1,w2,b1,b2],[dw,db,dw1,dw2,db1,db2])
 )

5 开始训练

 for i in range(50000):
     y1,c1=g([0,0],0)
     y2,c2=g([0,1],1)
     y3,c3=g([1,0],1)
     y4,c4=g([1,1],0)
     print  c1+c2+c3+c4
     print y1,y2,y3,y4

6 结果输出：

0.000541548001074
[ 0.01069522] [ 0.98782012] [ 0.98784247] [ 0.01144574]
0.000541536246431
[ 0.01069511] [ 0.98782025] [ 0.9878426] [ 0.01144562]

可以看到，每一项都接近[0 1 1 0],网络已经成功训练了。

交叉熵的结果输出

0.00187006124627
[ 0.00044582] [ 0.99958399] [ 0.99938235] [ 0.00039013]

相同参数下，很明显交叉熵的结果更好！