【Python】2.13学习笔记 数学函数和随机函数

我死了，今天看课看过头了，忘了发作业，被典明批评

而且化学作业还是瞎搞的，直接就发了

我觉得我已经提前死亡了，现在不死亡，开学也会的

函数

挺容易的，有很多语言之间重合的部分

注意

在使用某些数学函数以前，要使用这一语句

import math

使用随机数前，得调用另一个

import random

\(import\)的作用是调用一个库

例如之前的

import keyword

和\(C++\)里的

#include<bits/stdc++.h>

类似

而且在使用库中的函数时，需要加“库的名称.”

例如开方函数需要写成

math.sqrt()

不加\(math.\)会报错

库：

封装一些功能

同一库里的函数功能相似

绝对值函数

\(abs\)函数，搞竞赛的时候不是很常用（其实是我太菜了

print( abs( -19260817 ) ) #顺带一提，19260817是一个质数

这个函数不在\(math\)库中，它是内建函数

大于小于

真则返回1,假则返回0

不用调用\(math\)库

\(max,min\)函数

\(max\)字面意思，返回给定参数较大值

但是和\(C++\)不一样的是，可以同时比较多个

a1 = 1
a2 = 2
a3 = 3
a4 = 4444  #我又来迫害米4达了
print( max( a1, a2, a3, a4 ) )

返回值是4444

\(min\)同理

不用调用\(math\)

乘方

要计算\(2^5\)

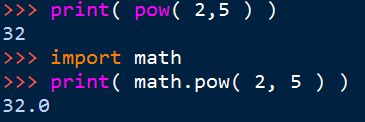
print( pow( 2, 5 ) )

这个有意思了，pow函数有两个

第一个可以直接使用，整数运算

print( pow( 2, 5 ) )

第二个不能直接用，要调用\(math\)库

会保留小数位

print( math.pow( 2, 5 ) )

四舍五入函数

可以规定位数，只要加一个参数就行，但是默认不加的话，就是保留整数位

print( round( 3.14159 ) ) # 输出3
print( round( 3.14159, 2 ) ) # 输出3.14

注意这个函数不在\(math\)库中

元组函数

啥是元组呢，就是整数部分加浮点数部分的形式

print( math.modf( 22.7 ) )

返回的整数部分与浮点数部分都是浮点数

虽然会有鬼畜的精度错误……

开方函数

上面写过了

print( math.sqrt( 16 ) )

返回的依然是浮点数

随机数函数

随机数函数有很多

使用前务必调用\(random\)库

\(choice\)函数

从序列的元素里随机挑选一个

也可以挑字符串，混搭也可以

print( random.choice( [ 1, 3, 5, 7, 9, "屁桃" ] ) )
print( random.choice( range( 5 ) ) )  #range(5) == [ 0, 1, 2, 3, 4 ]

但是需要注意的是，如果写成下面这样，便不会再把这个字符串看成一个元素，而是每个字母都看成一个元素

print( random.choice( "aCutePig" ) )

\(randrange\)函数

从指定范围内，按基数递增选数目

print( random.randrange( 1, 100, 5 ) )

从\(1\)到\(99\)中，选取\(1 + 5n\)的数，例如\(6,11,16,21\)

print( random.randrange( 1, 100, 2 ) )

选取\(1,3,5,7\)等等

开始的范围和基数可以不写，开始默认是0，基数默认是1

\(random\)函数

随机生成一个小于\(1\)大于等于\(0\)的浮点数

print( random.random() )

\(shuffle\)函数

打乱（简明易懂

list = [ 1, 2, 3, 4, 5 ] #生成一个列表
random.shuffle( list ) #打乱列表元素顺序

\(uniform\)函数

生成一个闭区间内的任意实数（浮点数或整数

当然，和无穷无尽的浮点数比起来，整数的个数显得太过可怜

我在\(1\)到\(100\)间生成了\(100\)个数都没有一个整数(不排除人品问题

print( random.uniform( 1, 100 ) )