使用 Helm【转】

Helm 安装成功后，可执行 helm search 查看当前可安装的 chart。

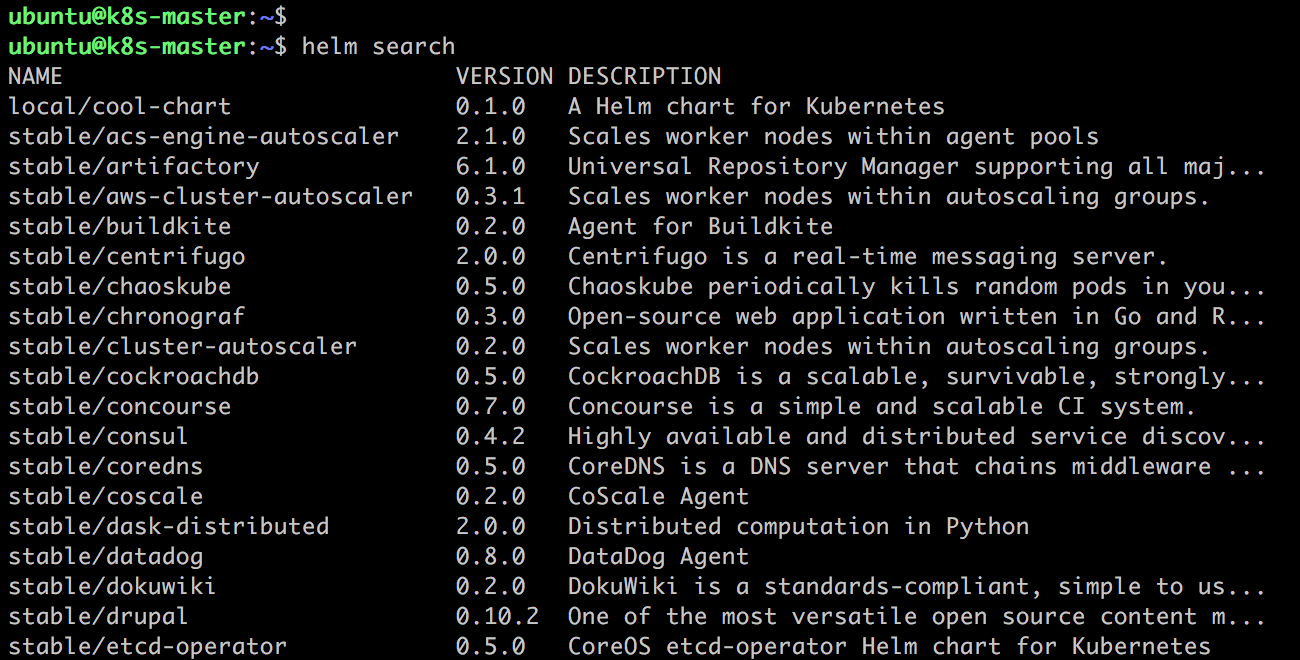
这个列表很长，这里只截取了一部分。大家不禁会问，这些 chart 都是从哪里来的？

前面说过，Helm 可以像 apt 和 yum 管理软件包一样管理 chart。apt 和 yum 的软件包存放在仓库中，同样的，Helm 也有仓库。

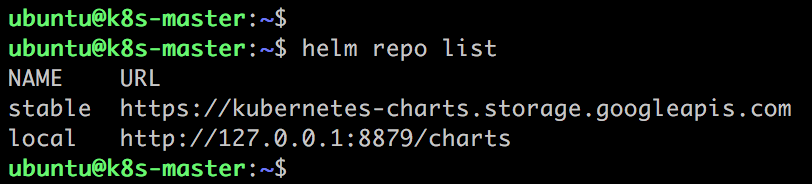
Helm 安装时已经默认配置好了两个仓库：stable 和 local。stable 是官方仓库，local 是用户存放自己开发的 chart 的本地仓库。

helm search 会显示 chart 位于哪个仓库，比如 local/cool-chart 和 stable/acs-engine-autoscaler。

用户可以通过 helm repo add 添加更多的仓库，比如企业的私有仓库，仓库的管理和维护方法请参考官网文档 https://docs.helm.sh

与 apt 和 yum 一样，helm 也支持关键字搜索：

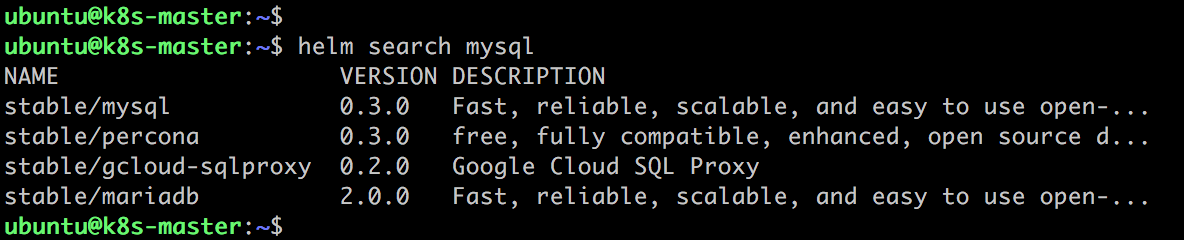
包括 DESCRIPTION 在内的所有信息，只要跟关键字匹配，都会显示在结果列表中。

安装 chart 也很简单，执行如下命令可以安装 MySQL。

helm install stable/mysql

如果看到如下报错，通常是因为 Tiller 服务器的权限不足。

执行如下命名添加权限：

kubectl create serviceaccount --namespace kube-system tiller

kubectl create clusterrolebinding tiller-cluster-rule --clusterrole=cluster-admin --serviceaccount=kube-system:tiller

kubectl patch deploy --namespace kube-system tiller-deploy -p '{"spec":{"template":{"spec":{"serviceAccount":"tiller"}}}}'

然后再次执行

helm install stable/mysql

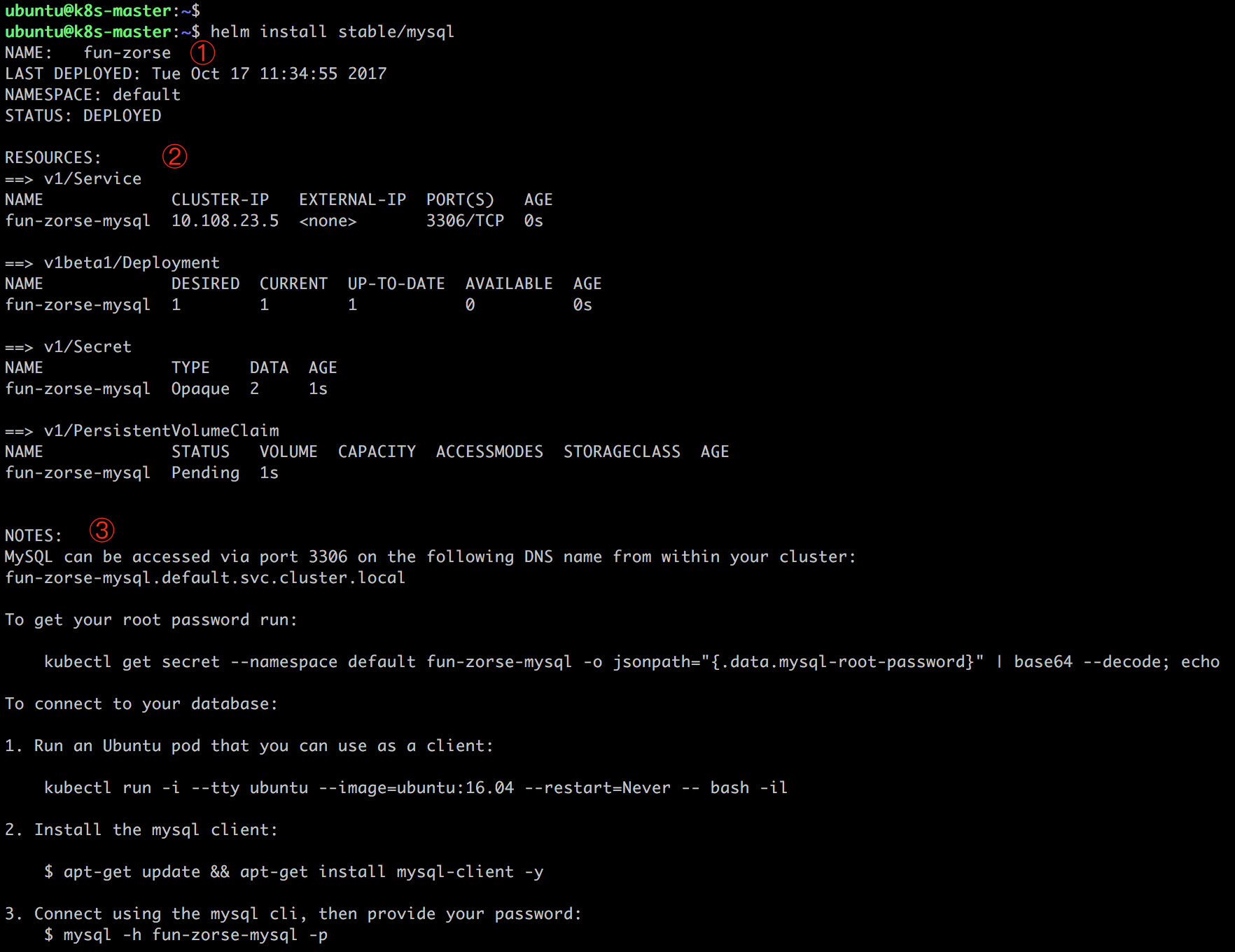
输出分为三部分：

① chart 本次部署的描述信息：

NAME 是 release 的名字，因为我们没用 -n 参数指定，Helm 随机生成了一个，这里是 fun-zorse。

NAMESPACE 是 release 部署的 namespace，默认是 default，也可以通过 --namespace 指定。

STATUS 为 DEPLOYED，表示已经将 chart 部署到集群。

② 当前 release 包含的资源：Service、Deployment、Secret 和 PersistentVolumeClaim，其名字都是 fun-zorse-mysql，命名的格式为 ReleasName-ChartName。

③ NOTES 部分显示的是 release 的使用方法。比如如何访问 Service，如何获取数据库密码，以及如何连接数据库等。

通过 kubectl get 可以查看组成 release 的各个对象：

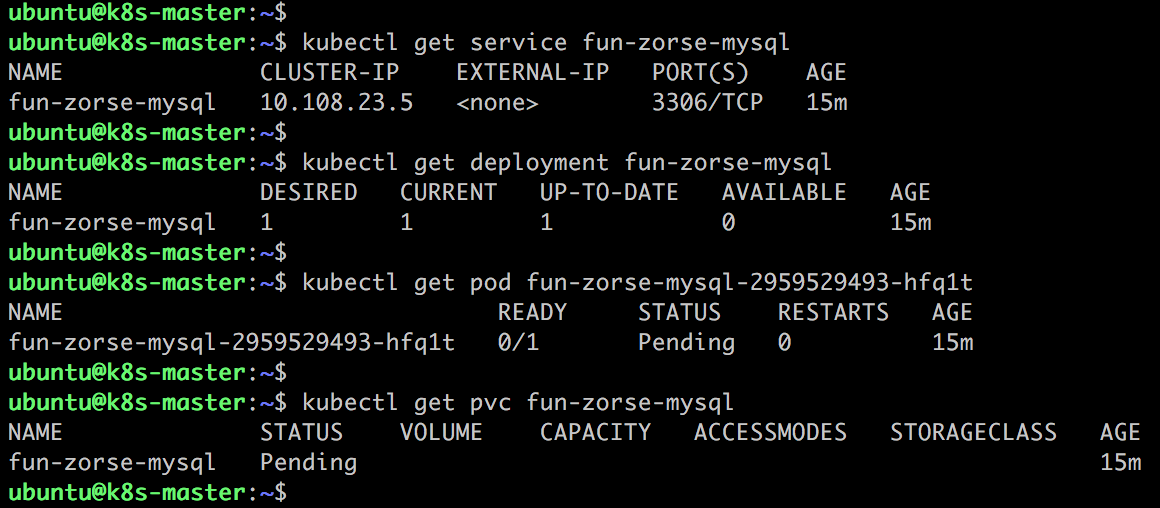
因为我们还没有准备 PersistentVolume，当前 release 还不可用。

helm list 显示已经部署的 release，helm delete 可以删除 release。

Helm 的使用方法像极了 apt 和 yum，用 Helm 来管理 Kubernetes 应用非常方便。

chart 是 Helm 的应用打包格式，下节我们详细介绍。