LQR要点

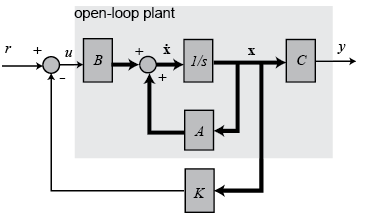
新的“A”变成着了这样：Ac = A - KB

基于对象：状态空间形式的系统

能量函数Ｊ：也称之为目标函数

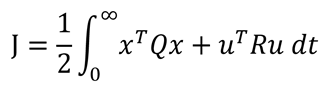
Q：半正定矩阵，对角阵（允许对角元素出现０）

R：正定矩阵，QR其实就是权重

下面这段话可能会加深对LQR的理解：

当ｘ是一维的，Ｊ就变成

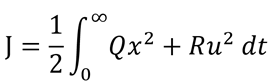
我们的目的是使能量函数J最小，那么Ｑｘ＾２和Ｒｕ＾２都要最小，则t趋近无穷时，x要趋近0，要保证Ｑｘ＾２为一个最小定值那么Ｑ要很大，Ｑ越大ｘ衰减速度也就越快；同理增大Ｒ，ｕ就会变小，对系统的控制变弱，ｘ衰减速度将会变慢

如何选取QR？

无一般规律可寻，一般取决设计者的经验，在这提供几个选择的原则：

1 Q、R都是对称矩阵，Q为正半定矩阵，R为正定矩阵

2 通常选取Q、R为对角矩阵，实际应用，通常将R值固定，通过改变Q的值来调制最优，当控制量只有一个，R就变成一个标量，一般取值1

为了更好的选取Q/R，我进行了一些尝试，发现如下：

假设我们的状态量是x1，x2，现在改变系数，观察对x1的影响

关于Q与R的

1 同时Q=>kQ，R=>kr，对x1无影响；

2 单取Q=>kQ或R=>R/k，产生的影响相同；

3 增大Q，对x1的控制力加强；

关于Q内部的

1 增大x1的系数，对x1的控制力加强；

2 增大x2的系数，x1基本不变；

3 减小x2的系数，对x1控制力减弱，以至到达目标状态的时间变长；（试验中对x1的第一步控制较强，但之后控制力明显减弱，可能是由于我给的初始量不太符合客观现实）

计算反馈矩阵K的步骤：

1 选择QR矩阵

2 求解Riccati方程的P（P是公式推导过程中设的矩阵，目的就是方便求K，在这求出P就能求出K）

3 计算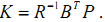（在matlab中给定Ａ，Ｂ，Ｑ，Ｒ用ｌｑｒ函数可直接计算出Ｋ）

（实际控制中我们无法调用lqr函数，求解K本质上属于求解Riccati方程，详见我的随笔：Riccati方程迭代法求解）

ｕ（ｋ）＝－Ｋ＊ｘ（ｋ），ｕ（ｋ）控制完将会得到一个新的ｘ（ｋ＋１），周而复始可不断求出ｕ

调节目标：将状态调节到零，而不是系统误差为零

下面有一个倒立摆控制器的例子

其状态变量是[p p' Θ Θ‘]，p是小车位移。Θ是倒立摆角度

A = [0 1 0 0

0 0 -1 0

0 0 0 1

0 0 9 0];

B = [0;0.1;0;-0.1];

C = [0 0 1 0];   %观测角度

D = 0;

Q = [1 0 0 0

0 1 0 0

0 0 10 0

0 0 0 10   ];

R = 0.1;

%由上面这个系统，可以计算出K

K = lqr(A,B,Q,R);

Ac = A - B*K;

%对系统进行模拟

x0 = [0.1;0;0.1;0]; %初始状态

t = 0:0.05:20;

u = zeros(size(t));

[y,x]=lsim(Ac,B,C,D,u,t,x0);

plot(t,y);

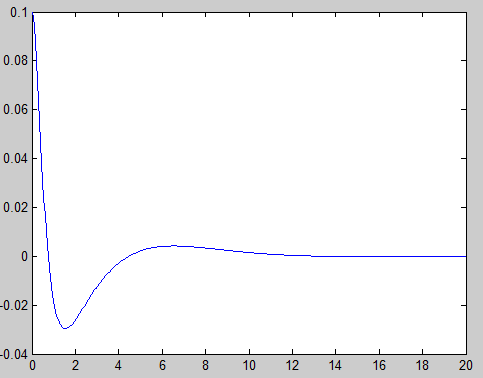
系统的控制效果与系统状态空间的准确度、QR的选取有极大关系！！！

也可采用u(k+1) = -K_lqr * x(k)和x(k+1) = A * x(k) + B * u的方式尝试跑自己的例子