verilog求倒数-ROM实现方法

采用线性逼近法结合32段线性查找表的方式来实现1/z的计算。

首先将1/32-1/64的定点化数据存放到ROM中，ROM中存放的是扩大了2^20 次方的数字四舍五入后的整数部分。n值越大，精度越大，误差越小。这里取n=20；

ROM中存储的数据是1/（32+i）*2^20的四舍五入的整数部分。

32-64间的数据可以通过查表来实现，其他的数据则采用的是线性逼近的方法。

线性逼近的步骤为：

1.确定最高非零比特位的位置

2.对z进行左移或者右移，得到zp

3.zp查找ROM，得到1/zp，以及1/（zp+1），

4.求的1/zp-1/（zp+1），为误差A

5.N=z-zp*2^(m-5)

6.B=A/2^（m-5）*N

7.将扩大的部分缩小回去，或者缩小了的放大回去，那么1/z=(1/zp-B)*(1/2^(m-5))

代码插入：

module top_inv(
    input clk,syn_rst,
    input [:]dataa,
    input [:]datab,
    //input [20:0]ampout,
    output reg [:]inv
   // output reg done
    );
    reg [:] address1;
    reg [: ]address2;
    wire [:] m;
   // wire done;
    reg [:]invr;
    reg [:] ampout_r;
    reg [:] ampout_r1;
    wire [:] ampout;
    reg [:] ampoutr1,ampoutr2,ampoutr3,ampoutr4;
    wire [:] inv_r1;
    wire [:] inv_r2;
    reg [:] diff_r;
    reg [:] diffr;
    reg [:] diff;
    reg [:] N;
    reg [:] N1;
    reg en;

  always @(posedge clk or negedge syn_rst)
  begin
    if(~syn_rst)
    begin
    ampoutr1<='d0;
    ampoutr2<='d0;
    ampoutr3<='d0;
    ampoutr4<='d0;
    end
    else
    ampoutr1<=ampout;
    ampoutr2<=ampoutr1;
    ampoutr3<=ampoutr2;
    ampoutr4<=ampoutr3;
  end
  reg [:] inv_r1t1,inv_r1t2,inv_r1t3;
 always@(posedge clk or negedge syn_rst)
 begin
    if(~syn_rst)
    begin
        inv_r1t1<=;
        inv_r1t2<=;
        inv_r1t3<=;
    end
    else
    begin
        inv_r1t1<=inv_r1;
        inv_r1t2<=inv_r1t1;
        inv_r1t3<=inv_r1t2;
    end
 end
 reg [:] mt1,mt2,mt3,mt4,mt5;
 always@(posedge clk or negedge syn_rst)
 begin
    if(~syn_rst)
    begin
        mt1<=;
        mt2<=;
        mt3<=;
        mt4<=;
        mt5<=;
    end
    else
    begin
        mt1<=m;
        mt2<=mt1;
        mt3<=mt2;
        mt4<=mt3;
        mt5<=mt4;
    end
 end
 reg sel;
 reg selr1,selr2;
  always @(posedge clk or negedge syn_rst)
  begin
      if(~syn_rst)
      begin
         diff<=;
         diffr <= ;
         ampout_r<='b0;
         ampout_r1<=;
         address1<='b0;
         address2<='b0;
         en<=;
         sel<=;
      end
      else
      begin
     // if(done)
      //begin
        if((ampout>=)&&(ampout<=))
            begin
                ampout_r<=;
                ampout_r1<=;
                address1<=ampoutr3-;
                address2<= ;
                diff <= ;
                diffr <= ;
                N <= ;
                N1<= ;
                en<=;//不需要计算m的值
                sel<=;
                selr1<=;
                selr2<=;
            end
        else
            begin
             en<=;//需要计算m的值
             if(m>)
             begin
                // ampoutrr<=ampout;
                 ampout_r<=ampoutr1>>(m-);
                 ampout_r1<=ampout_r;//zp
                 address1<=ampout_r-;///inv_r1
                 address2<=ampout_r-;///inv_r2
                 diff <= inv_r1-inv_r2;
                 diffr <=diff;
                 N1<=ampout_r1<<(mt2-);
                 N<=ampoutr4-N1;
                 selr1<=;
                 selr2 <= selr1;
                 sel <= selr2;
             end
             if(m<)
             begin
                  //ampoutrr<=ampout;
                  ampout_r<=ampoutr1<<(-m);//     mt4   mt3    mt2
                  ampout_r1 <= ampout_r;//          N    N1    ampout_r1
                  address1<=ampout_r-;///mt4                 inv_r1
                  address2<=ampout_r-;//inv_r1t3             inv_r2    mt1
                  diff <= inv_r1-inv_r2;//diff_r<<diffr<<diff<<address<<ampout_r<<  m  <<ampout
                  diffr <=diff;        //                      ampoutr3 ampoutr2  ampoutr1
                  N1<=ampout_r1>>(-mt2);
                  N<=ampoutr4-N1;
                  selr1<=;
                  selr2 <= selr1;
                  sel <= selr2;
              end
          end
          end
     // end
      end
//  assign diff=sel?(inv_r1-inv_r2):'b0;
  //assign N=sel?(ampout-N1):0;
  //assign diff_r = en?(diff*N>>(m-5)):0;
  //assign diff_r = (m>5)?(diff*N>>(m-5)):(diff*N<<(5-m));
 // assign inv = sel?(inv_r1-diff_r)>>(m-5):inv_r1;

  always@(posedge clk or negedge syn_rst)
  begin
      if(~syn_rst)
      begin
        invr<=;
      //  done<=0;
      diff_r<=;
      end
      else
      begin
        if(sel) begin

            if(m>)begin
                diff_r <= diffr*N>>(mt4-);
                invr<=(inv_r1t3-diff_r)>>(mt5-);
         //       done<=1;
                end
            else begin
                diff_r <= diffr*N<<(-mt4);
                invr<=(inv_r1t3-diff_r)<<(-mt5);
         //       done<=1;
                end
            end
        else
        begin
            diff_r<=;
            invr<=inv_r1t3;
        end
      end
  end
 always@(posedge clk or negedge syn_rst)
 begin
    if(~syn_rst)
    begin
        inv<=;
    end
    else
    begin
        if(invr)
            inv<= invr;
        else
            inv<=inv;
    end
 end
 //ROM 核的例化

 rom u_rom(.clk(clk),
           .address1(address1),
           .address2(address2),
           .inv_r1(inv_r1),
           .inv_r2(inv_r2)//,
           //.c(c)
       );
 //例化寻找最高非零位
 not_0 u_not_0 (
 // port map - connection between master ports and signals/registers
     .ampout(ampout),
     .clk(clk),
     .m(m),
     .en(en),
     .syn_rst(syn_rst)
 );
complex_abs u_comlex_abs(
       .clk(clk),
       .syn_rst(~syn_rst),
       .dataa(dataa),
       .datab(datab),
       .ampout(ampout)
       );
endmodule

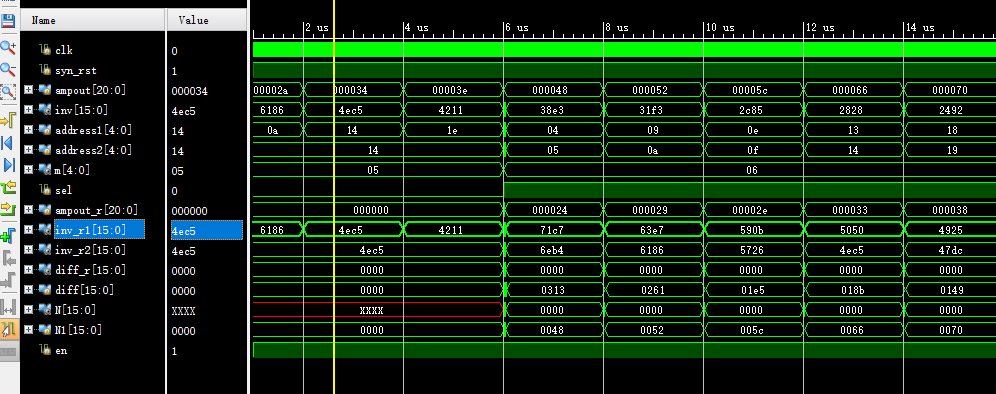
那么最终的仿真结果：如果直接查询的话，结果输出延时一个时钟周期，如果线性逼近的方法得到，延时3-5个时钟周期，这里周期设定为20ns；

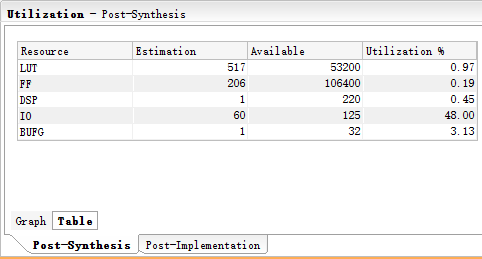
占用资源报告：

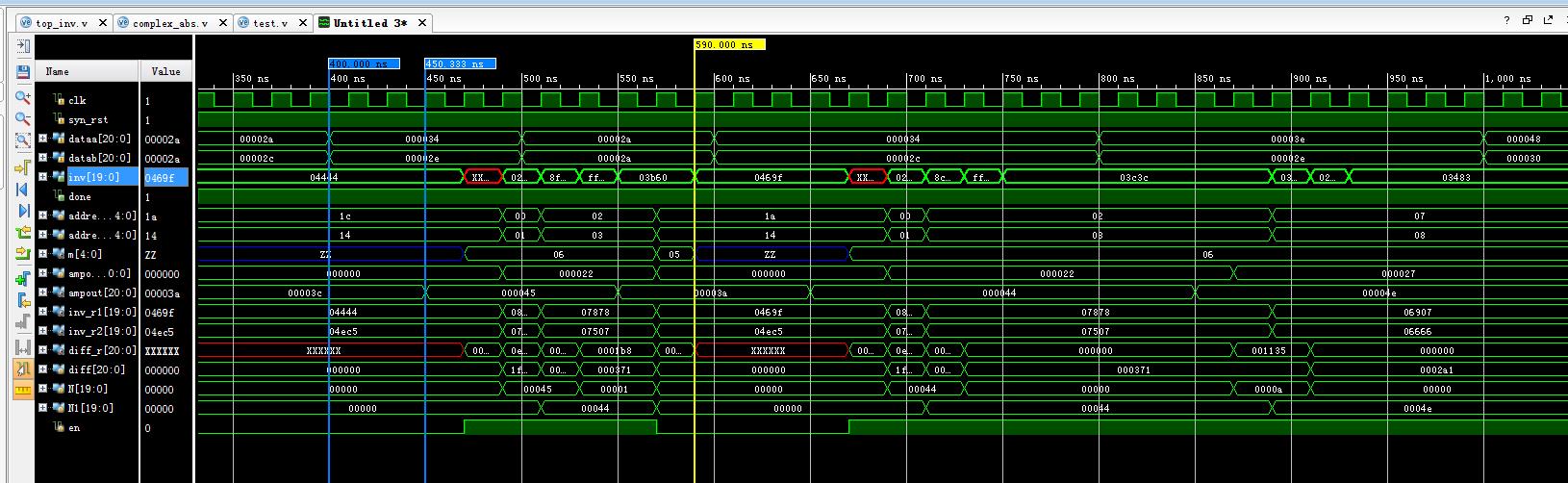
增加一个求平方根的模块以后的仿真结果（数据输入后，一共需要约10个时钟周期才可以计算出一个平方更求导数值）。有一个小疑问就是怎么添加一个标志信号，让我们知道哪里输出的inv 信号是有效的