Miller_Rabin素性测试

1. 为什么需要素性测试？

我们其实已经知道有一些判断素数的方法，比如：

遍历测试：待测试数n与2，3，...√n做除法判断余数是否为零，如果没有任何一个数可以整除n，则说明n为素数

Wilson定理：对于给定的正整数n，n是素数的充要条件为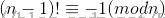，则可以通过判断这个方程是否成立来判断n是否为素数

上面的方法都可以确定的判断出一个数是否为素数，但问题在于对于大整数，这两个算法都需要很大计算量和时间，能不能有一个更快速的判定算法呢？

答案是当前还没有一个更高效且能准确判定素数的方法。但借助随机算法和数论知识，已有可以非常高效且判定错误率很低的素数测试算法，即Millan_Rabin素性测试

2. 需要知道的知识

2.1 Fermat定理

费马定理的前提是a和n互质。当n本身就是素数的时候如果a<n那么a和n始终互素，费马定理是成立的，但n当不是素数，且a和n不互素的话不能用费马定理（也就是说费马定理不一定成立）

需要知道的是满足费马定理是素数的必要条件，但不是充分条件，也就是说是素数一定满足费马定理（如果一个数不满足费马定理就不是素数），但是满足费马定理的数字不一定是素数（称为伪素数，伪素数的数量较少，所以可以通过费马定理以比较大的概率判定一个数是否为素数）

令a=2，不满足2^(n-1) mod n = 1的n一定不是素数；如果满足的话则多半是素数。这样，一个比试除法效率更高的素性判断方法出现了：制作一张伪素数表，记录某个范围内的所有伪素数，那么所有满足2^(n-1) mod n = 1且不在伪素数表中的n就是素数。之所以这种方法更快，是因为我们可以使用二分法快速计算2^(n-1) mod n 的值，这在计算机的帮助下变得非常容易；在计算机中也可以用二分查找有序数列、Hash表开散列、构建Trie树等方法使得查找伪素数表效率更高。

那么伪素数的个数到底有多少？换句话说，如果我只计算2^(n-1) mod n的值，事先不准备伪素数表，那么素性判断出错的概率有多少？统计表明，在前10亿个自然数中共有50847534个素数，而满足2^(n-1) mod n = 1的合数n有5597个。这样算下来，算法出错的可能性约为0.00011。这个概率还是太高了，如果想免去建立伪素数表的工作，我们需要还需要改进素性判断的算法。

最简单的想法就是，我们刚才只考虑了a=2的情况。对于式子a^(n-1) mod n，取不同的a可能导致不同的结果。一个合数可能在a=2时通过了测试，但a=3时的计算结果却排除了素数的可能。于是，人们扩展了伪素数的定义，称满足a^(n-1) mod n = 1的合数n叫做以a为底的伪素数(pseudoprime to base a)。前10亿个自然数中同时以2和3为底的伪素数只有1272个，这个数目不到刚才的1/4。这告诉我们如果同时验证a=2和a=3两种情况，算法出错的概率降到了0.000025。容易想到，选择用来测试的a越多，算法越准确。通常我们的做法是，随机选择若干个小于待测数的正整数作为底数a进行若干次测试，只要有一次没有通过测试就立即把这个数扔回合数的世界。这就是Fermat素性测试。

    人们自然会想，如果考虑了所有小于n的底数a，出错的概率是否就可以降到0呢？没想到的是，居然就有这样的合数，它可以通过所有a的测试（在满足费马定理前提的条件下）。Carmichael第一个发现这样极端的伪素数，他把它们称作Carmichael数。你一定会以为这样的数一定很大。错。第一个Carmichael数小得惊人，仅仅是一个三位数，561。前10亿个自然数中Carmichael数也有600个之多。Carmichael数的存在说明，我们还需要继续加强素性判断的算法。

2.2 二次探测定理

这个定理应该怎么理解呢？其实就是说，(x+1)(x-1)可以整除p，又因为p是素数，不可分割，所以要么是(x-1)这一部分整除了p（因为0<x<p，故x-1<p，所以x-1只能为0才能满足，所以此时x = 1），要么就是(x+1)整除了p（因为0<x<p，则1<x+1<p+1，故只有当x+1=p才能满足，此时x = p-1），所以满足条件的x=1或x=p-1

二次探测定理可以用来对费马定理做一个增强，以更高的概率确定一个数是否为素数，将两者融合，就可以得到Miller_Rabin算法。

3. Miller_Rabin定理

为什么说测试次数为k次，错误概率可降低之(1/4)^k呢？（这还是保守估计）

我的理解是，因为上面我们知道，同时通过2和3的费马测试的伪素数个数不到通过2的费马测试的个数的1/4，这还只是通过了费马测试，这里我们还进行了二次检测，所以错误率应该更低，且数字越大，能够同时通过更多数字费马测试的数越少（推测），所以错误率至少是(1/4)^k，实际中应该比这个还要低很多。

下面举个例子来说明Miller_Rabin算法判断素数的流程，我们来测试341是否为素数。首先可以验证341可以通过以2为底的Fermat测试，因为2^340 mod 341=1。如果341真是素数的话，那么2^170 mod 341只可能是1或340；当算得2^170 mod 341确实等于1时，我们可以继续查看2^85除以341的结果。我们发现，2^85 mod 341=32，这一结果并不满足x = 1或x = 340这一条件，所以和二次探测定理矛盾，这一结果摘掉了341头上的素数皇冠。

    Miller-Rabin素性测试同样是不确定算法，我们把可以通过以a为底的Miller-Rabin测试的合数称作以a为底的强伪素数(strong pseudoprime)。第一个以2为底的强伪素数为2047。第一个以2和3为底的强伪素数则大到1 373 653。所以说Miller_Rabin算法可以看作Fermat测试的一个加强版，可以以更大的概率确定一个数是否为素数。再借助快速幂算法，同时可以加速这个进程，判定速度更快。

4. Miller_Rabin算法C++实现

#include <iostream>
#include <stdlib.h>
typedef long long int ll;
using namespace std;

ll quick_mul (ll a, ll b, ll mod) {
    ll res = ;
    while(b) {
        if(b & ) {
            res = (res + a) % mod;
        }
        a = (a + a) % mod;
        b >>= ;
    }
    return res;
}

ll quick_pow(ll a, ll n, ll mod) {
    ll res = ;
    while(n) {
        if(n & ) {
            res = quick_mul(res, a, mod);
        }
        a = quick_mul(a, a, mod);
        n >>= ;
    }
    return res;
}

bool Miller_Rabin(ll n) {
    if(n == ) {
        return true;
    }
    if(n <  || !(n & )) {
        return false;
    }
    ll m = n-, k = ;
    while(!(m&)) {
        k++;
        m >>= ;
    }
//    printf("m = %lld, k = %lld\n", m, k);
    int iter = ;
    for(int i = ; i < iter; i++) {
        ll a = rand() % (n-) + ;
//        printf("a = %lld\n", a);
        ll x = quick_pow(a, m, n);
//        printf("x = %lld\n", x);
        ll y;
        for(int j = ; j < k; j++) {
            y = quick_pow(x, x, n);
//            printf("y = %lld\n", y);
            if(y ==  && x !=  && x != n-) {
                return false;
            }
            x = y;
        }
        if(y != ) {
            return false;
        }
    }
    return true;
}

int main(void) {
    ll num;
    printf("Please input the num you want to test:\n");
    scanf("%lld", &num);
    printf("%s\n", Miller_Rabin(num) ? "yes" : "no");
}

参考

https://blog.csdn.net/ECNU_LZJ/article/details/72675595

http://www.matrix67.com/blog/archives/234

本文很大程度参考了这两篇博文，都写的很好，值得学习:）