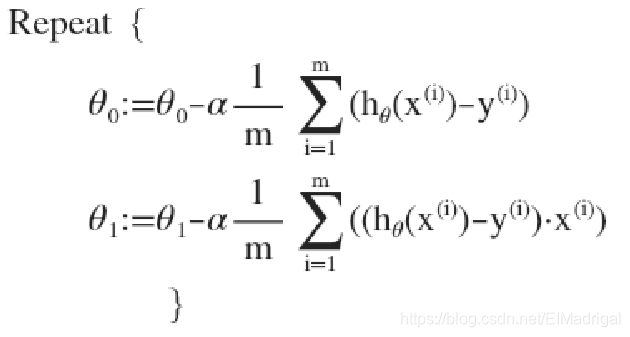#Week2 Linear Regression with One Variable
一、Model Representation
还是以房价预测为例,一图胜千言:
h表示一个从x到y的函数映射。
二、Cost Function
因为是单变量线性回归,所以假设函数是:
\]
所以接下来的问题是怎样确定参数\(\theta_0\)和\(\theta_1\)?
这两个参数会决定我们的模型预测值与训练集的实际数据的差距,这就是建模误差。
那么在回归问题中,代价函数选择如下的平方误差函数比较合理:
\]
m是训练集的样本数目,\(x^{(i)}\)是每个房子的尺寸,\(y^{(i)}\)是实际价格。
只要寻找使得\(J(\theta_0,\theta_1)\)最小的参数即可。
之所以要除以2,主要是为了后续的梯度下降法求导时抵消平方的那个2。
三、Gradient Descent
为了求得代价函数的最小值,采用梯度下降法。
- 用一个随机的参数组合计算\(J\)
- 找到一个使得\(J\)下降最多的参数组合,更新参数,直到找到一个局部最优解
就像下山一样,每次都走一步,每次选择下降最快的方向直到局部最低。
在批量梯度下降算法(所有的训练样本都要用到)中,同步更新所有参数:
\(\alpha\)是学习率,表示每一步走多长。
如果\(\alpha\)太小,那么更新的过程就会很缓慢;如果\(\alpha\)太大,可能跳过最低点,导致发散。
当接近局部最优时,由于斜率会越来越小,所以每一步会自动走得很小,不需要减小学习率\(\alpha\)。
四、Gradient Descent For Linear Regression
对之前得回归模型应用梯度下降算法:
对\(J(\theta_0,\theta_1)\)求关于\(\theta_0\)、\(\theta_1\)的偏导数,带入参数更新公式,有:
#Week2 Linear Regression with One Variable的更多相关文章
- Stanford机器学习---第二讲. 多变量线性回归 Linear Regression with multiple variable
原文:http://blog.csdn.net/abcjennifer/article/details/7700772 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- Stanford机器学习---第一讲. Linear Regression with one variable
原文:http://blog.csdn.net/abcjennifer/article/details/7691571 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回归 ...
- 机器学习笔记1——Linear Regression with One Variable
Linear Regression with One Variable Model Representation Recall that in *regression problems*, we ar ...
- Machine Learning 学习笔记2 - linear regression with one variable(单变量线性回归)
一.Model representation(模型表示) 1.1 训练集 由训练样例(training example)组成的集合就是训练集(training set), 如下图所示, 其中(x,y) ...
- Ng第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 2.4 梯度下降 2.5 梯度下 ...
- 【cs229-Lecture2】Linear Regression with One Variable (Week 1)(含测试数据和源码)
从Ⅱ到Ⅳ都在讲的是线性回归,其中第Ⅱ章讲得是简单线性回归(simple linear regression, SLR)(单变量),第Ⅲ章讲的是线代基础,第Ⅳ章讲的是多元回归(大于一个自变量). 本文的 ...
- MachineLearning ---- lesson 2 Linear Regression with One Variable
Linear Regression with One Variable model Representation 以上篇博文中的房价预测为例,从图中依次来看,m表示训练集的大小,此处即房价样本数量:x ...
- 斯坦福第二课:单变量线性回归(Linear Regression with One Variable)
二.单变量线性回归(Linear Regression with One Variable) 2.1 模型表示 2.2 代价函数 2.3 代价函数的直观理解 I 2.4 代价函数的直观理解 I ...
- 机器学习 (一) 单变量线性回归 Linear Regression with One Variable
文章内容均来自斯坦福大学的Andrew Ng教授讲解的Machine Learning课程,本文是针对该课程的个人学习笔记,如有疏漏,请以原课程所讲述内容为准.感谢博主Rachel Zhang的个人笔 ...
随机推荐
- 家庭记账本app进度之关于tap的相关操作1
今天还主要学习关于怎样制作微信的先关的tap. 今天的主要成果是已经了解了相关的技术,以及相关的思路.代码经过一个下午的编写,基本接近尾声. 更详细的实验代码,以及相关的知识点将在明天完善后进行发表. ...
- Python zipfile模块学习
转载自https://www.j4ml.com/t/15270 import zipfile import os from zipfile import ZipFile class ZipManage ...
- 动态网页D-html
BOM(Browser Object Model)浏览器对象模型 window对象(window – 代表浏览器中打开的一个窗口) 1.alert()方法 – 定义一个消息对话框 window.ale ...
- 【一统江湖的大前端(9)】TensorFlow.js 开箱即用的深度学习工具
示例代码托管在:http://www.github.com/dashnowords/blogs 博客园地址:<大史住在大前端>原创博文目录 目录 一. 上手TensorFlow.js 二. ...
- Threejs从入门到入门
前言threejs官网:https://threejs.org/ github各个版本:https://github.com/mrdoob/three.js/tags 版本更迭很快,我用的时候还是r9 ...
- asp.net core webapi Session 内存缓存
Startup.cs文件中的ConfigureServices方法配置: #region Session内存缓存 services.Configure<CookiePolicyOptions&g ...
- SSH proxycommand 不在同一局域网的机器ssh直连
本地和192.168.1.10不在同一个网络,可以通过jumpserver跳转过去,操作如下 选项 -L 本机端口 -f 后台启用,可以在本机直接执行命令,无需另开新终端 -N 不打开远程shell, ...
- 用scrapy实现模拟登陆
class Test1sSpider(scrapy.Spider): name = 'test1s' allowed_domains = ['yaozh.com'] start_urls = ['ht ...
- vnpy源码阅读学习(9)回到OptionMaster
回到OptionMaster 根据我们对APP调用的代码阅读,我们基本上知道了一个APP是如何被调用,那么我们回到OptionMaster学习下这个APP的实现. 看看结构 class OptionM ...
- 教你如何快速让浏览器兼容es6
写在正文前,本来这一节的内容应该放在第二节更合适,因为当时就有同学问ES6的兼容性如何,如何在浏览器兼容ES6的特性,这节会介绍一个抱砖引玉的操作案例. 为什么ES6会有兼容性问题? 由于广大用户使用 ...