粒子群优化算法(PSO)之基于离散化的特征选择(FS)（三）

作者：Geppetto

前面我们介绍了特征选择(Feature Selection，FS)与离散化数据的重要性，总览的介绍了PSO在FS中的重要性和一些常用的方法，介绍了FS与离散化的背景，介绍本文所采用的基于熵的切割点和最小描述长度原则(MDLP)。今天我们来学习利用PSO来进行离散化特征选择的一些方法。今天我们会介绍EPSO与PPSO。

EPSO和PPSO都遵循图一所示的基本步骤。初始化后，对粒子进行迭代评估和更新，直到满足停止条件为止。为了对粒子进行评价，首先对训练数据进行离散化，并根据进化的切点选择特征。然后将转换后的数据放入学习算法中，计算出适应度。基于这种适应性，pbest和gbest被更新并用于更新粒子的位置。

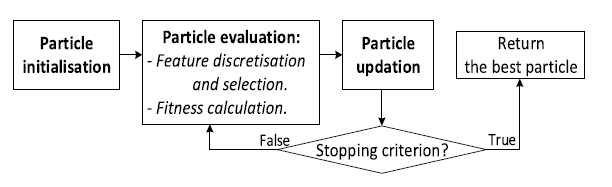
图一

在这两种方法中离散化和FS步骤的工作原理是相同的。为实现离散化，如果特征值小于某个截点，则将其转换为0；否则，它就是1。如果一个特性的所有值都转换为相同的离散值，那么它就被认为是一个无关的特性，因为它不能区分不同类的实例。FS是通过消除这些无用的特性来完成的。在整个离散化数据的分类性能改进的基础上，对剩余的离散特征进行了评价。

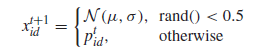
A.EPSO

EPSO的主要思想是使用BBPSO直接演化出一个可以在相应的特征值范围[MinF···MaxF]内任何值的切点。每个粒子的位置表示一个候选解，它是一个与问题的维数相对应的n维的实向量。图二给出了一个粒子位置及其相应候选解的例子。在这个例子中，粒子的第一个维度，表示第一个特性(F1)的切割点，需要在范围内有一个值[8.5,25.7]。如果一个特性F的更新点超出了这个范围，它将被设置到最近的边界。

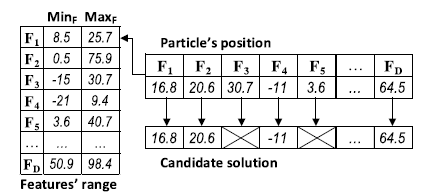
图二

（1）粒子初始化：由于在高维数据上的多变量离散化的搜索空间是巨大的。这意味着对于那些在初始候选方案中未被选中的特性，它们的切点将被设置为相应特性的最大值。对于其他选择的特性，它们的切点是使用满足MDLP的最好的基于熵的切割点初始化的。原则上，它们可以根据对应特性范围内的任何值进行初始化。然而，完全随机的初始切点可能导致收敛速度较慢。此外，特征的最佳切点的信息增益是其相关性的指标。因此，具有较大信息增益的特性在初始化过程中被选择的概率更大。

（2）粒子评价：基于粒子所产生的切点，训练数据转换为离散值的新训练集和较少的特征数，这要归功于消除特征，其切割点等于最小值或最大值。例如，在图2中，F3切割点等于它的最大值，F5的切点等于它的最小值，这两个特征都将被丢弃。

然后根据转换训练集的分类精度，对每个粒子的离散化和FS解进行评估，通过对整个离散数据的评估，提出的方法可以对所有选定特征的分割点进行评估，同时考虑特征交互。适应度函数采用平衡分类精度，如下:

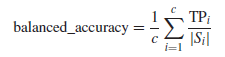
其中c是问题的类数，TPi是i类中正确识别的实例数，|Si|是类i的样本量，所有类的权重均为1/c。

B.PPSO

在EPSO中，BBPSO可以自由地在相应的范围内生成一个剪切点。这可能会导致一个巨大的搜索空间，特别是在多维数据的多变量方法中。因此，为了将搜索空间缩小到高度潜在的区域，在PPSO中，我们使用BBPSO来从每个特性的潜在断点中选择一个切点。潜在的切点是基于熵的切点，它们的信息增益满足前面所讲的MDLP准则。每个特征可能有不同数量的可能的切割点，它们被计算并存储在一个可能的切点表中。图3给出了该表和粒子位置以及相应候选方案的示例。每个粒子位置都是一个整数向量，表示所选的剪切点索引。因此，向量的大小等于原始特征的数量，而进化的值需要介于1和相应特征的潜在的切点数量之间。例如，在图3中，第一个特性(F1)有两个可能的剪切点，索引1和2。因此，粒子的第一个维度需要落在范围[1,2]。如果它是2，那么切割点6.8被选择来离散F1。

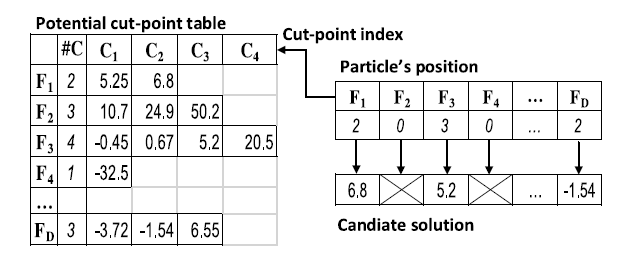
图三

在更新过程中，如果一个维度的更新值不在切点索引范围之外，则将其设置为0，这表明相应的特性没有一个好的切点，因此应该被忽略。

（1）粒子初始化：每个粒子位置都被初始化为一个随机特征子集，其中有一些被选中的特征，它们的切点索引与0不同。选中的特性将会将它们的切点索引设置为最佳MDLP剪切点的索引。与EPSO相似，具有较高信息增益的特性将有更高的选择机会。

为了使PPSO通用到所有的问题，PPSO使用一个限制的大小为所有数据集。然后在进化过程中，当BBPSO似乎卡在局部最优，如果当前的gbest fitness比最后一个gbest fitness至少有10%的优势，BBPSO将被重新设置为更大的尺寸（缩放机制）。这个机制的目的是开始搜索小的特性子集，同时打开更大更好的功能子集的机会。

（2）粒子评估：基于每个特性的选定的切点索引，从潜在的切点表中检索出切点值。然后用它来离散相应的特征。但是，如果一个特性的进化的剪切点索引为0，那么该特性就被认为是未被选中的。因此，在图3中，本例中没有选择F2和F4。

在EPSO中，分类精度被用来作为衡量每个粒子的适应度指标。这可能很难区分类与类之间的边界相当大的情况，使许多不同的模型获得相同的精度。此外，虽然包装器方法能够产生高精度的解决方案，但过滤方法通常更快、更普遍。将这两种方法的强度结合在评价函数中，有望产生更好的解决方案。此外，结合这两种方法，还可以更好地区分特征子集之间的细微差别，提供更平滑的适应度环境以方便搜索过程。然而，简单地结合这些措施在计算上可能是不切实际的。因此，我们需要找到一种聪明的方法来组合它们，而不需要更多的运行时间。在常用的滤波方法中，距离是一种多变量测量方法，可以对特征集的判别能力进行评估，并将其作为KNN的基本测量方法。因此，将该方法与KNN包装方法结合起来不会增加计算时间，因为距离测量只计算一次，但使用两次。

适应度函数使用两种平衡分类精度和距离测量加权系数(μ)与测量的距离,如下所示,用于最大化之间的距离不同的类的实例(DB)和减少之间的距离相同的类的实例(DW)。DB和DW采用以下公式计算:

其中Dis(Vi, Vj)是两个向量Vi和Vj之间的距离。在本文中，我们使用两个二进制向量之间的匹配或重叠的比例作为它们之间的距离。

参考文献：

文章：“A New Representation in PSO for Discretization-Based Feature Selection”

作者：Binh Tran, Student Member, IEEE, Bing Xue, Member, IEEE, and Mengjie Zhang, Senior Member, IEEE