【字符串算法】字典树(Trie树)

什么是字典树

基本概念

字典树，又称为单词查找树或Tire树，是一种树形结构，它是一种哈希树的变种，用于存储字符串及其相关信息。

基本性质

1.根节点不包含字符，除根节点外的每一个子节点都包含一个字符

2.从根节点到某一节点。从根节点到该节点路径上经过的字符连接起来，就是该节点对应的字符串

3.同一个节点的所有子节点包含的字符都不相同

运用方面

典型应用是用于统计，排序和保存大量的字符串(不仅限于字符串)，经常被搜索引擎系统用于文本词频统计。

优点缺点

字典树是经典的空间换时间的数据结构，利用字符串的公共前缀来减少查询时间，最大限度的减少无谓的字符串比较，查询效率据说比哈希树高。

但缺点就很显然了，就是空间比较大……

举个栗子

什么不太了解，没事，让我们来结合栗子来分析一下！

我们首先读入四个字符串

ba

b

band

abc

在没有读入前，我们有一个空空的根节点；

接着我们插入单词ba；

接着插入单词b，由于根节点有连向b的子节点，所以只需路径上的s++就好了；

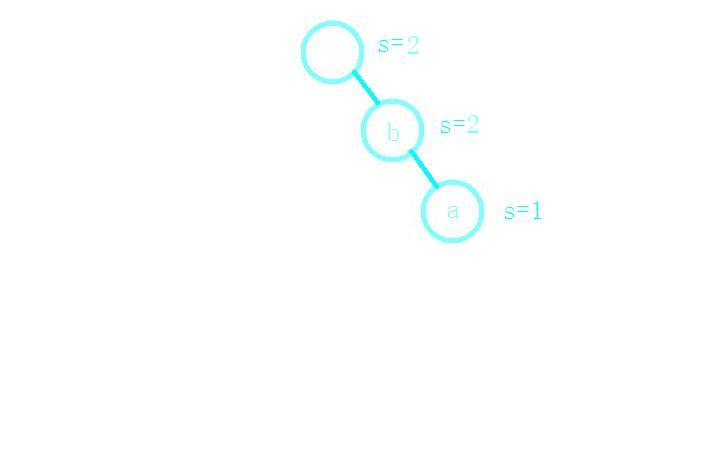
接着插入单词bank，ba之前就有，只需s++，而nk需要在ba后添加子节点完成存储；

最后插入单词abc；

如何构造字典树

我们来结合程序一步一步来构造这棵可爱的字典树吧！！

构造节点

我们需要运用struct来存储字典树上每个节点的信息：

struct node
{
    int s,v[27]，val;
    node()
    {
        s=0;
        memset(v,-1,sizeof(v));
    }
}t[410000];

s是用来存储有多少个单词进过了这个节点，v是用来存储这个点从a到z的儿子节点分别在哪，而val则是存储这个节点的权值，至于权值代表什么，就要依照题目灵活变换了。

构造字典树

我们先抛出程序：

int bt(int root)
{
    int len=strlen(a+1);int x=root;
    for(int i=1;i<=len;i++)
    {
        int y=a[i]-'a'+1;//将a^z转化为1^26
        if(t[x].v[y]==-1)t[x].v[y]=++tot;
        x=t[x].v[y];t[x].s++;
    }
}

首先我们先读入了一个字符串a，它的长度为len；

接着我们对于它的字符进行循环处理，当我们处理到这个字符串的第i个字符的时候，我们要进行分类讨论——

我们用x存储第i-1个字符在字典树中的位置；

当我的前一个字符没有指向我的字符的时候，我就tot++，在字典树中开创一个新的空间，我就把自己放在这个空间里；

如果我的前一个字符有指向我的字符的子节点时，我就放心地走到那个子节点就好了；最后记得更新x的值为当前处理的子节点的位置，并且s++，表示又多了一个单词进过了这个节点，以及完成val的修改之类的工作；

i++，进入下一重循环！

这样一棵完整的字典树就出来了！

模板&&模板题

【caioj 1463】统计前缀

题目描述

【题意】

给出很多个字符串(只有小写字母组成)和很多个提问串，统计出以某个提问串为前缀的字符串数量(单词本身也是自己的前缀).

【输入格式】

输入n,表示有n个字符串(n<=10000)

接下来n行,每行一个字符串,字符串度不超过10

输入m,表示有m个提问(m<=100)

第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.

【输出格式】

对于每个提问,给出以该提问为前缀的字符串的数量.

【样例输入】

5

banana

band

bee

absolute

acm

4

ba

b

band

abc

【样例输出】

2

3

1

0

就是一道裸题，查询时输出对应节点的s就好了；

附上代码：

#include<bits/stdc++.h>
using namespace std;
struct node
{
    int s,v[27];
    node()
    {
        s=0;
        memset(v,-1,sizeof(v));
    }
}t[410000];
char a[410000];
int i,j,k,m,n,tot,js,jl;

int bt(int root)
{
    int len=strlen(a+1);int x=root;
    for(int i=1;i<=len;i++)
    {
        int y=a[i]-'a'+1;
        if(t[x].v[y]==-1)t[x].v[y]=++tot;
        x=t[x].v[y];t[x].s++;
    }
}

int solve(int root)
{
    int len=strlen(a+1);int x=root;
    for(int i=1;i<=len;i++)
    {
        int y=a[i]-'a'+1;
        if(t[x].v[y]==-1)return 0;
        x=t[x].v[y];
    }
    return(t[x].s);
}

int main()
{
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%s",a+1);
        bt(0);
    }

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",a+1);
        printf("%d\n",solve(0));
    }
}

结语

通过这篇BLOG相信你已经掌握了Trie树，那就向着AC自动机前进吧！希望你喜欢这篇BLOG！

字典树练习题：

HDU1251（本题原版）

HDU1075

HDU1800

参考

https://ethsonliu.com/2019/09/trie-tree.html

https://oi-wiki.org/string/trie/