熵权法原理及matlab代码实现

参考原理博客地址https://blog.csdn.net/u013713294/article/details/53407087

一、基本原理

在信息论中，熵是对不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。

根据熵的特性，可以通过计算熵值来判断一个事件的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响（权重）越大，其熵值越小。

二、熵值法步骤

1. 选取n个国家，m个指标，则为第i个国家的第j个指标的数值（i=1,
2…, n; j=1,2,…, m）；

2. 指标的归一化处理：异质指标同质化

由于各项指标的计量单位并不统一，因此在用它们计算综合指标前，先要对它们进行标准化处理，即把指标的绝对值转化为相对值，并令，从而解决各项不同质指标值的同质化问题。而且，由于正向指标和负向指标数值代表的含义不同（正向指标数值越高越好，负向指标数值越低越好），因此，对于高低指标我们用不同的算法进行数据标准化处理。其具体方法如下:

正向指标:

负向指标:

则为第i个国家的第j个指标的数值（i=1, 2…, n; j=1,
2,…, m）。为了方便起见，归一化后的数据仍记为;

3. 计算第j项指标下第i个国家占该指标的比重：

4. 计算第j项指标的熵值：

其中. 满足;

5. 计算信息熵冗余度：

6. 计算各项指标的权值：

7. 计算各国家的综合得分：

注：对正逆指标归一化的时候如果采用的方法不一样，正指标归一化得到的值会大一些，逆指标的归一化得到的值会小一些，然后算权重，逆指标对应的权重也会相应的小，从而逆指标对应的得分也小些，就相当于对逆指标进行了处理。如果对正逆指标归一化采用的方法一样，为了体现逆指标的不利影响，最后应该总分减去逆指标的得分的。两种方法不同，但都是为了体现逆指标对综合得分的不利影响。

matlab代码实现及其注释

https://github.com/wangjiwu/entropy-method-matlab-

只需要更改相应的data 和 指标矩阵即可

main.m 主函数

clc;
load shang_datas  % load the data

%加载数据  列数表示指标数 ， 行数表示评价的个体数
%此数据 7个评价个体 3个评价指标
X = shang_datas 

%说明指标是正向指标还是负向指标
%此数据第一个是负向指标， 其余为正向指标
Ind=[2 1 1]; %Specify the positive or negative direction of each indicator

%S 为分数排名 W为指标权重
[S,W]=shang(X,Ind) % get the score

其他函数请查看github项目地址

运行结果

我使用的数据是 3个指标， 7个待评价个体



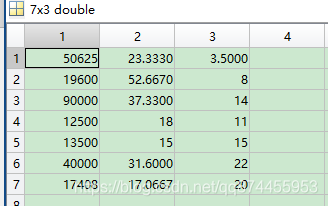
进行处理后得到 7个待评价个体的分数和 指标所占的权重