4.13 省选模拟赛 树 树形dp 卷积 NTT优化dp.

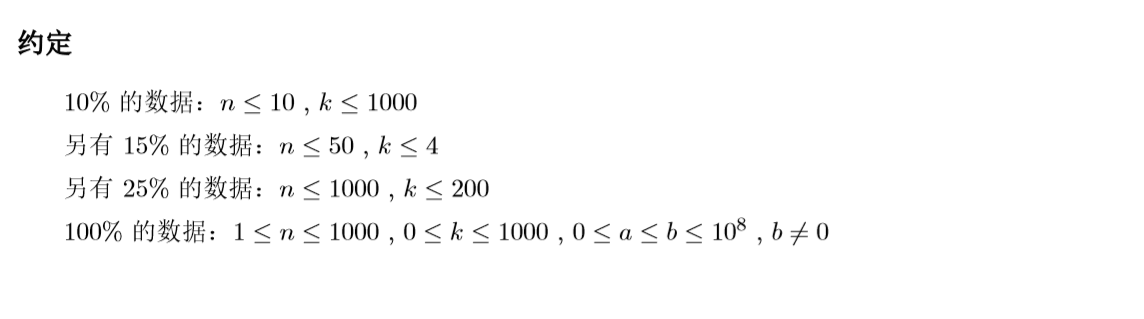
考试的时候 看到概率 看到期望我就怂 推了一波矩阵树推自闭了 发现 边权点权的什么也不是。

想到了树形dp 维护所有边的断开情况 然后发现数联通块的和再k次方过于困难。

这个时候 应该仔细观察一下 和再k次方之后会出现什么 容易发现是一个类似隔板法的东西。

也就是 选出k个点的集合 集合可重 代价为点权之积.

只需要把所有的情况都做出来就行了。

至于联通块考虑一个一个统计贡献。

这也就是说 对于每一个联通块来说我们指定一个根节点来统计 要不然会算重。

不难发现以每个点的子树内部为联通块 可以不重不漏的计算。

设状态 f[i][j]表示 i所在的连通块选出了j个点权的点权积之和.

容易发现转移 \(f[i][j]=(1-p)\cdot f[i][j]+\sum_{k=0}{j}f[x][k]\cdot f[tn][j-k]\cdot C(j,k)\)

为什么 后面要乘一个组合数 显然考虑将k次方展开之后 这其实是一个排列 那么方案数为 j!。

但是 f[x][k]中这k个数已经算了排列的数量了 同理f[tn][j-k]也是 所以可以把他们看成标号相同的点 所以各自要除以各自的阶乘。

显然每个点对答案的贡献为 (1-pfa)*f[x][k].

容易发现转移是一个卷积形式的 NTT优化即可。

const int MAXN=2050,G=3;
int n,k,len,ans,lim;
//int f[MAXN][MAXN]; f[i][j]表示以i为根的子树内 i所在的连通块中选出了j项的权值积之和.
//有 f[i][j]=(1-p)f[i][j]+f[tn][x]*f[i][j-x]*C(j,x) 显然是一个卷积NTT优化.
int f[MAXN][MAXN],b[MAXN],rev[MAXN],g[MAXN];
int fac[MAXN],inv[MAXN],A[MAXN],B[MAXN];
int lin[MAXN<<1],ver[MAXN<<1],nex[MAXN<<1],e[MAXN<<1];
inline int ksm(int b,int p){int cnt=1;while(p){if(p&1)cnt=(ll)cnt*b%mod;p=p>>1;b=(ll)b*b%mod;}return cnt;}
inline void add(int x,int y,int z)
{
	ver[++len]=y;
	nex[len]=lin[x];
	lin[x]=len;
	e[len]=z;
}
inline void NTT(int *a,int op)
{
	rep(0,lim-1,i)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(int len=2;len<=lim;len=len<<1)
	{
		int wn=ksm(G,op==1?(mod-1)/len:mod-1-(mod-1)/len);
		int mid=len>>1;
		for(int j=0;j<lim;j+=len)
		{
			int d=1;
			for(int i=0;i<mid;++i)
			{
				int x=a[i+j],y=(ll)a[i+j+mid]*d%mod;
				a[i+j]=(x+y)%mod;a[i+j+mid]=(x-y+mod)%mod;
				d=(ll)d*wn%mod;
			}
		}
	}
	if(op==-1)
	{
		int inv=ksm(lim,mod-2);
		rep(0,lim-1,i)a[i]=(ll)a[i]*inv%mod;
	}
}
inline void mul(int *a,int *b)
{
	rep(0,lim-1,i)
	{
		A[i]=(ll)a[i]*inv[i]%mod;
		B[i]=(ll)b[i]*inv[i]%mod;
	}
	NTT(A,1);NTT(B,1);
	rep(0,lim-1,i)g[i]=(ll)A[i]*B[i]%mod;
	NTT(g,-1);
}
inline void dp(int x,int fa,int fp)
{
	f[x][0]=1;
	rep(1,k,i)f[x][i]=((ll)f[x][i-1]*b[x])%mod;
	go(x)
	{
		if(tn==fa)continue;
		dp(tn,x,e[i]);
		mul(f[x],f[tn]);
		rep(0,k,j)
		{
			f[x][j]=(ll)(1-e[i]+mod)*f[x][j]%mod;
			f[x][j]=((ll)f[x][j]+(ll)g[j]*fac[j]%mod*e[i]%mod)%mod;
		}
	}
	ans=(ans+(ll)f[x][k]*(1-fp+mod)%mod)%mod;
}
int main()
{
	freopen("1.in","r",stdin);
	get(n);get(k);
	rep(1,n,i)get(b[i]);
	rep(2,n,i)
	{
		int get(x);int get(y);
		int get(a);int get(b);
		a=(ll)a*ksm(b,mod-2)%mod;
		add(x,y,a);add(y,x,a);
	}
	fac[0]=1;
	rep(1,k,i)fac[i]=(ll)fac[i-1]*i%mod;
	inv[k]=ksm(fac[k],mod-2);
	fep(k-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
	lim=1;while(lim<=k+k)lim=lim<<1;
	rep(1,lim-1,i)rev[i]=rev[i>>1]>>1|((i&1)?lim>>1:0);
	dp(1,0,0);put(ans);return 0;
}