4.18 省选模拟赛 无聊的计算器 CRT EXBSGS EXLucas

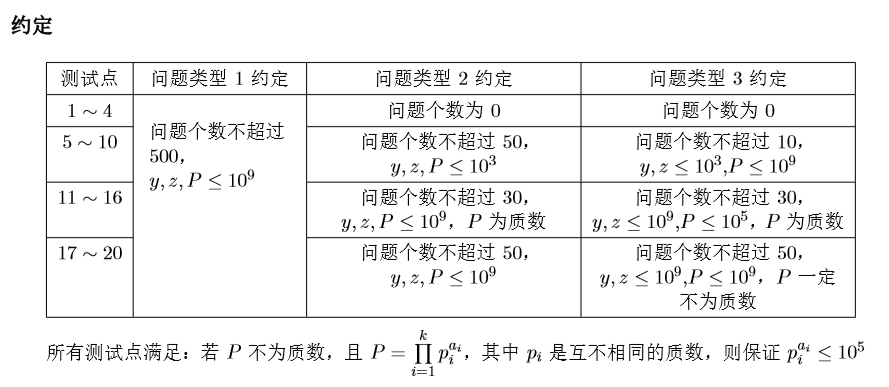
算是一道很毒瘤的题目 考试的时候码+调了3h才搞定。

op==1 显然是快速幂。

op==2 有些点可以使用BSGS 不过后面的点是EXBSGS.

这个以前学过了 考试的时候还是懵逼。(当时还是看着花姐姐的题解学的

为了起到再次复习的作用 我决定 再推导一遍。

对于高次同余方程 \(a^x\equiv b(mod p)\) 朴素的BSGS利用是欧拉定理的应用解决的。此时要求(a,p)=1.

考虑解决(a,p)>1的情况 容易发现我们进行一些操作 使得他们互质就可以继续使用EXBSGS了。

当b%p==1时显然x取0 但是当b%p!=1时x有解必然取的时正整数 原式可以变成 \(a^{x-1}\cdot a+kp=b\)

容易发现 当(a,p)|b 等式才有整数解。

当出现上述情况的时候 容易把式子变为 \(a^{x-1}\cdot \frac{a}{(a,p)}\equiv \frac{b}{(a,p)}(mod \frac{p}{(a,p)})\)

可以发现两个式子求解出x后时等价的。

然后如果x和p'还不互质继续下去。直至互质然后解EXBSGS即可。

最后要加回来一直递归下去的次数 可以发现最多递归log层。

值得注意的是再递归的时候如果发现了某一部(a,p)不整除b了 那么还是无解的注意判断。

最后 关于求逆 不是质数了 注意使用exgcd.

op==3.

裸的EXLucas了 也写过很多遍了。值得一提的是 提前预处理跑的是真的快。

const ll MAXN=200010;
ll Q;
ll op,a,b,p,xx,yy;
map<ll,ll>H;
ll y[MAXN],w[MAXN],jc[MAXN],f[MAXN],inv[MAXN],ans[MAXN];
ll flag;
inline void fj(ll x)
{
	flag=0;
	for(ll i=2;i*i<=x;++i)
	{
		if(x%i==0)
		{
			y[++flag]=i;w[flag]=1;
			while(x%i==0)
			{
				x/=i;
				w[flag]*=i;
			}
		}
	}
	if(x>1)y[++flag]=x,w[flag]=x;
}
inline ll ksm(ll b,ll p,ll mod)
{
	ll cnt=1;
	while(p)
	{
		if(p&1)cnt=cnt*b%mod;
		b=b*b%mod;p=p>>1;
	}
	return cnt;
}
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline void exgcd(ll a,ll b)
{
	if(!b){xx=1;yy=0;return;}
	exgcd(b,a%b);
	ll zz=xx;xx=yy;yy=zz-a/b*yy;
}
inline ll INV(ll a,ll mod)
{
	exgcd(a,mod);
	return (xx%mod+mod)%mod;
}
inline ll BSGS(ll a,ll b,ll mod)//a^x=b(% mod)
{
	a%=mod;b%=mod;
	if(b==1)return 0;
	H.clear();
	ll m=(ll)sqrt(mod*1.0)+1;
	ll w1=1;H[b]=0;
	rep(1,m,i)
	{
		w1=w1*a%mod;
		ll cc=w1*b%mod;
		H[cc]=max(H[cc],i);
	}
	ll cc=1;
	rep(1,m,i)
	{
		cc=cc*w1%mod;
		if(H.find(cc)!=H.end())
			return i*m-H[cc];
	}
	return -1;
}
inline ll exBSGS()
{
	a%=p;b%=p;
	if(b==1)return 0;
	ll k=0;
	ll wp=p,w1=1,g;
	while((g=gcd(a,wp))>1)
	{
		if(b%g)return -1;
		++k;w1=a/g;b=b/g;wp=wp/g;
		b=b*INV(w1,wp)%p;
		if(b==1)return k;
	}
	ll ans=BSGS(a,b,wp);
	return ans<0?ans:ans+k;
}
inline ll C(ll a,ll b,ll mod)
{
	return ((jc[a]*inv[b]%mod)*(inv[a-b]))%mod;
}
inline void prepare(ll mod)
{
	jc[0]=1;
	for(ll i=1;i<mod;++i)jc[i]=jc[i-1]*i%mod;
	inv[mod-1]=ksm(jc[mod-1],mod-2,mod);
	for(ll i=mod-2;i>=0;--i)inv[i]=inv[i+1]*(i+1)%mod;
}
inline ll Lucas(ll a,ll b,ll mod)
{
	if(a<b)return 0;
	if(a<=mod)return C(a,b,mod);
	return (Lucas(a%mod,b%mod,mod)*Lucas(a/mod,b/mod,mod))%mod;
}
inline ll lc(ll x,ll p,ll pp)
{
	if(x<=p)return f[x];
	ll ww=x/pp;
	return ksm(f[pp],ww,pp)*f[x%pp]%pp*lc(x/p,p,pp)%pp;
}
inline ll js(ll x,ll xx,ll xxx,ll mod)
{
	ll w=1;
	ll cnt=0;
	while(x>w)
	{
		w=w*mod;
		cnt+=x/w;
		cnt-=xx/w;
		cnt-=xxx/w;
	}
	return cnt;
}
inline void ycl(ll p,ll pp)
{
	f[0]=1;
	rep(1,pp,i)if(i%p)f[i]=f[i-1]*i%pp;
	else f[i]=f[i-1];
}
inline ll solve(ll a,ll b,ll p,ll pp)
{
	ll k=js(a,b,a-b,p);
	ll ans1,ans2,ans3;
	ans1=lc(a,p,pp);
	ans2=lc(b,p,pp);
	ans3=lc(a-b,p,pp);
	ans2=INV(ans2,pp);
	ans3=INV(ans3,pp);
	ans1=((((ans1*ans2%pp)*ans3)%pp)*ksm(p,k,pp))%pp;
	return ans1;
}
inline ll merge()
{
	ll an=0;
	for(ll i=1;i<=flag;++i)
	{
		ll M=p/w[i];
		ll ww=INV(M,w[i]);
		an=(an+((M*ww%p)*ans[i])%p)%p;
	}
	return an;
}
signed main()
{
	//freopen("1.in","r",stdin);
	freopen("calculator.in","r",stdin);
	freopen("calculator.out","w",stdout);
	get(Q);
	rep(1,Q,i)
	{
		get(op);get(a);get(b);get(p);
		if(op==1)putl(ksm(a,b,p));
		if(op==2)
		{
			fj(p);ll ww;
			if(flag==1&&y[1]==w[1])ww=BSGS(a,b,p);
			else ww=exBSGS();
			if(ww<0)puts("Math Error");
			else putl(ww);
		}
		if(op==3)
		{
			swap(a,b);
			fj(p);
			if(flag==1&&y[1]==w[1])
			{
				prepare(p);
				putl(Lucas(a,b,p));
			}
			else
			{
				rep(1,flag,i)
				{
					ycl(y[i],w[i]);
					ans[i]=solve(a,b,y[i],w[i]);
				}
				putl(merge());
			}
		}
	}
	return 0;
}