NOIP2010pj三国游戏[博弈论]

题目描述

小涵很喜欢电脑游戏，这些天他正在玩一个叫做《三国》的游戏。

在游戏中，小涵和计算机各执一方，组建各自的军队进行对战。游戏中共有 N 位武将（N为偶数且不小于 4），任意两个武将之间有一个“默契值”，表示若此两位武将作为一对组合作战时，该组合的威力有多大。游戏开始前，所有武将都是自由的（称为自由武将，一旦某个自由武将被选中作为某方军队的一员，那么他就不再是自由武将了），换句话说，所谓的自由武将不属于任何一方。

游戏开始，小涵和计算机要从自由武将中挑选武将组成自己的军队，规则如下：小涵先从自由武将中选出一个加入自己的军队，然后计算机也从自由武将中选出一个加入计算机方的军队。接下来一直按照“小涵→计算机→小涵→……”的顺序选择武将，直到所有的武将被双方均分完。然后，程序自动从双方军队中各挑出一对默契值最高

的武将组合代表自己的军队进行二对二比武，拥有更高默契值的一对武将组合获胜，表示两军交战，拥有获胜武将组合的一方获胜。

已知计算机一方选择武将的原则是尽量破坏对手下一步将形成的最强组合，它采取的具体策略如下：任何时刻，轮到计算机挑选时，它会尝试将对手军队中的每个武将与当前每个自由武将进行一一配对，找出所有配对中默契值最高的那对武将组合，并将该组合中的自由武将选入自己的军队。下面举例说明计算机的选将策略，例如，游戏中一共有 6 个武将，他们相互之间的默契值如下表所示：

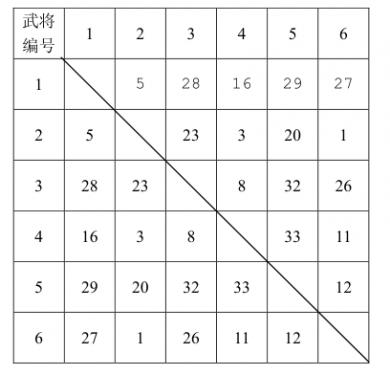
双方选将过程如下所示：

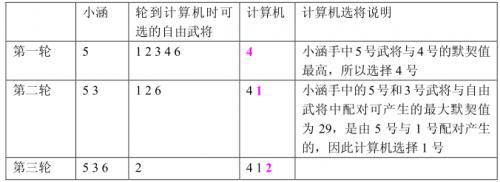
小涵想知道，如果计算机在一局游戏中始终坚持上面这个策略，那么自己有没有可能必

胜？如果有，在所有可能的胜利结局中，自己那对用于比武的武将组合的默契值最大是多

少？假设整个游戏过程中，对战双方任何时候均能看到自由武将队中的武将和对方军队的武将。为了简化问题，保证对于不同的武将组合，其默契值均不相同。

输入输出格式

输入格式：

输入文件名为 sanguo.in，共 N 行。

第一行为一个偶数 N，表示武将的个数。

第 2 行到第 N 行里，第（i+1）行有（Ni）个非负整数，每两个数之间用一个空格隔

开，表示 i 号武将和 i+1，i+2，……，N 号武将之间的默契值（0≤默契值≤1,000,000,000）。

输出格式：

输出文件 sanguo.out 共 1 或 2 行。

若对于给定的游戏输入，存在可以让小涵获胜的选将顺序，则输出 1，并另起一行输出

所有获胜的情况中，小涵最终选出的武将组合的最大默契值。

如果不存在可以让小涵获胜的选将顺序，则输出 0。

输入输出样例

输入样例#1：

【输入样例1】

6

5 28 16 29 27

23 3 20 1

8 32 26

33 11

12

【输入样例2】

8

42 24 10 29 27 12 58

31 8 16 26 80 6

25 3 36 11 5

33 20 17 13

15 77 9

4 50

19

输出样例#1：

【输出样例1】

1

32

【输出样例2】

1

77

说明

【数据范围】

对于 40%的数据有 N≤10。

对于 70%的数据有 N≤18。

对于 100%的数据有 N≤500。

对于任意一个武将 i ，假设与其默契最高的为j，其次为k，那么小涵要想拿到（i，j）是不可能的，拿到（i，k）确实100%的；同理，电脑想要拿到（i，j）与（i，k）都是不可能的。

每行取最大值

以后一定要分析

#include <iostream>

#include <cstdio>

#include <algorithm>

#include <cstring>

#include <cmath>

using namespace std;

const int N=;

inline int read(){

    char c=getchar();int x=,f=;

    while(c<''||c>''){if(c=='-')f=-;c=getchar();}

    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}

    return x*f;

}

int n,m,ans,a[N][N];

int main(){

    n=read();

    for(int i=;i<=n;i++)

        for(int j=i+;j<=n;j++) a[i][j]=a[j][i]=read();

    for(int i=;i<=n;i++){

        int t1=,t2=;

        for(int j=;j<=n;j++){

            if(a[i][j]>t1) t2=t1,t1=a[i][j];

            else if(a[i][j]>t2) t2=a[i][j];

        }

        ans=max(ans,t2);

    }

    printf("1\n%d",ans);

}