FFT原理及C++与MATLAB混合编程详细介绍

一：FFT原理

1.1 DFT计算

在一个周期内的离散傅里叶级数(DFS)变换定义为离散傅里叶变换(DFT)。

\[\begin{cases}
X(k) = \sum_{n=0}^{N-1}x(n)W_N^{kn}, & 0 \le k \le {N-1} \\
x(n) = \frac{1}{N} \sum_{k=0}^{N-1}X(k)W_N^{-kn}, & 0 \le n \le {N-1} \\
\end{cases}
\]

其中，\(W_N = e^{-j\frac{2\pi}{N}}\)。\(X(k)\)是\(x(n)\)的离散傅里叶变换。

用矩阵方程可以更加清楚的看出DFT的变换过程：

\[X = W \cdot x \tag{1}
\]

\(X = \begin{pmatrix}
X(0) \\
X(1) \\
x(2) \\
\vdots \\
X(N-1) \\
\end{pmatrix}\)；\(W = \begin{pmatrix}
1 & 1 & 1 & \cdots & 1 \\
1 & W_N^1 & W_N^2 & \cdots & W_N^{N-1} \\
1 & W_N^2 & W_N^4 & \cdots & W_N^{2(N-1)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & W_N^{N-1} & W_N^{2(N-1)} & \cdots & W_N^{(N-1)(N-1)} \\
\end{pmatrix}\)；\(x = \begin{pmatrix}
x(0) \\
x(1) \\
x(2) \\
\vdots \\
x(N-1) \\
\end{pmatrix}\)

可以看出，长度为\(N\)的有限长序列\(x(n)\)，其离散傅里叶变换\(X(k)\)仍是一个长度为\(N\)的有限长序列。由(1)可看出时间复杂度为\(O(N^2)\)，如果\(N = 1024\)点的话，需要1048576(一百多万)次复数乘法。DFT的计算量实在是太大了，于是有了后面的优化版本：快速傅里叶变换(FFT)。

1.2 FFT计算

1.2.1 性质铺垫

由于系数\(W_N^{nk} = e^{-j\frac{2\pi}{N}nk}\)是一个周期函数，可以用它的性质来改进算法，提高计算效率。

• 性质一：\(W_N^{k + \frac{N}{2}} = -W_N^k\) (对称性)

• 性质二：\(W_N^{nk} = W_1^{\frac{nk}{N}}\) (同除一个常数)

这里主要利用以上两个性质，把长度为N点的大点数的DFT运算依次分解为若干个小点数的DFT。因为DFT的计算量正比于\(N^2\)，\(N\)小计算量也小。

1.2.2 按时间抽取的基2FFT(N点)

假设进行FFT的点数N是2的整次方(基2)，首先将序列分为两组，一组为偶数项，一组为奇数项，然后进行如下的变换，推导如下：

\[\begin{align}
X(k) &= \sum_{n=0}^{N-1}x(n)W_N^{nk} \notag\\
&= \sum_{n=0为偶数}^{N-2}x(n)W_{N}^{nk} + \sum_{n=1为奇数}^{N-2}x(n)W_{N}^{nk} \notag\\
&= \sum_{r=0}^{\frac{N}{2}-1}x(2r)W_{N}^{2rk} + \sum_{r=0}^{\frac{N}{2}-1}x(2r+1)W_{N}^{(2r+1)k} \notag\\
&= \sum_{r=0}^{\frac{N}{2}-1}x(2r)W_{N}^{2rk} + W_N^k \sum_{r=0}^{\frac{N}{2}-1}x(2r+1)W_{N}^{2rk} （由性质二\downarrow）\notag\\
&= \sum_{r=0}^{\frac{N}{2}-1}x(2r)W_{\frac{N}{2}}^{rk} + W_N^k \sum_{r=0}^{\frac{N}{2}-1}x(2r+1)W_{\frac{N}{2}}^{rk} ，0 \le k \le \frac{N}{2} - 1 \tag{2}
\end{align}
\]

可以看出求\(x(n)\)的DFT变成了求其偶数项的DFT和奇数项的DFT的组合，但注意这只计算出了前一半的DFT值，后一半由如下性质得到：

由性质一\(\downarrow\)

\[X(k + \frac{N}{2}) = \sum_{r=0}^{\frac{N}{2}-1}x(2r)W_{\frac{N}{2}}^{rk} - W_N^k \sum_{r=0}^{\frac{N}{2}-1}x(2r+1)W_{\frac{N}{2}}^{rk} ，0 \le k \le \frac{N}{2} - 1 \tag{3}
\]

这样一来，我们就计算出了完整的\(x(n)\)的DFT值，其实这就是FFT的核心思想了，接下来我们用蝶形图让上面的计算步骤更直观形象一些。

1.3 蝶形信号流图

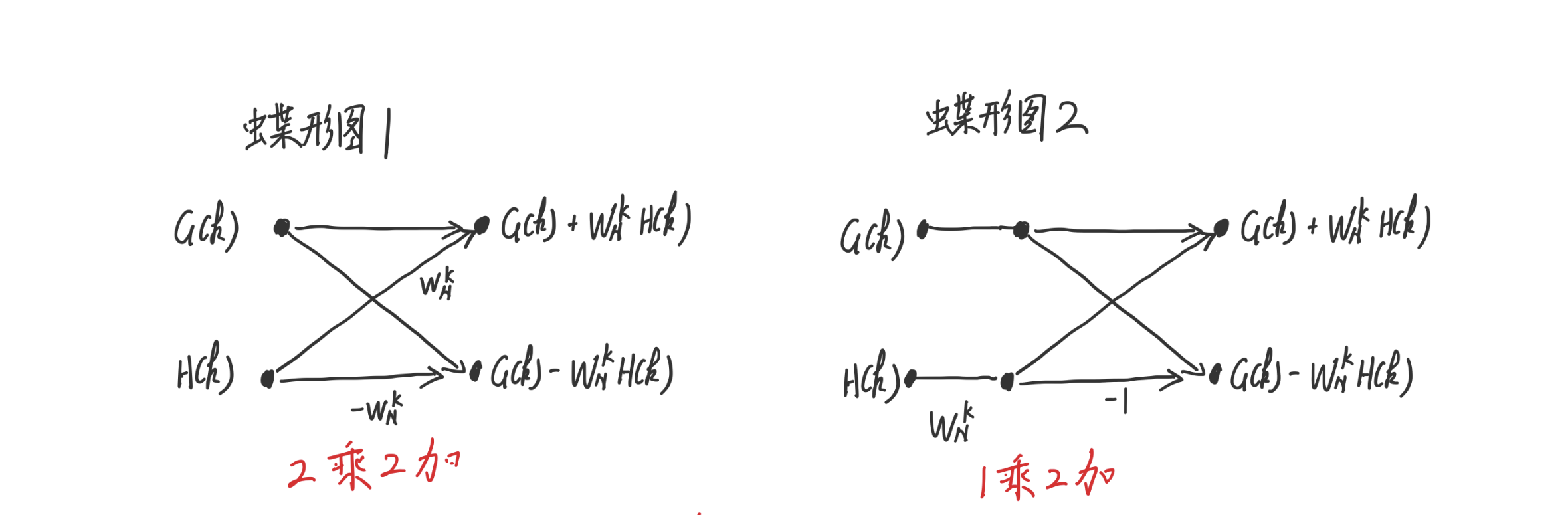
用\(G(k)\)代替偶数项DFT，用\(H(k)\)代替奇数项DFT，则整理公式(2)、(3)为：

\[\begin{cases}
X(k) = G(k) + W_N^k H(k)，& 0 \le k \le \frac{N}{2} - 1\\
X(k + \frac{N}{2}) = G(k) - W_N^k H(k), & 0 \le k \le \frac{N}{2} - 1 \tag{4} \\
\end{cases}
\]

其中

\[\begin{cases}
G(k) = \sum_{r=0}^{\frac{N}{2}-1}x(2r)W_{\frac{N}{2}}^{rk}\\
H(k) = \sum_{r=0}^{\frac{N}{2}-1}x(2r+1)W_{\frac{N}{2}}^{rk} \tag{5} \\
\end{cases}
\]

从（4）和（5）可以看出，我们可以把一串时域数据分成偶数部分和奇数部分来计算\(G(K)\)和\(H(k)\)，同样也可以再把偶数部分再分成偶数部分和奇数部分计算，直到分到最后只剩下两个数据，再递归计算出FFT结果，具体直观点的流程见下面经典的N点蝶形图：

---

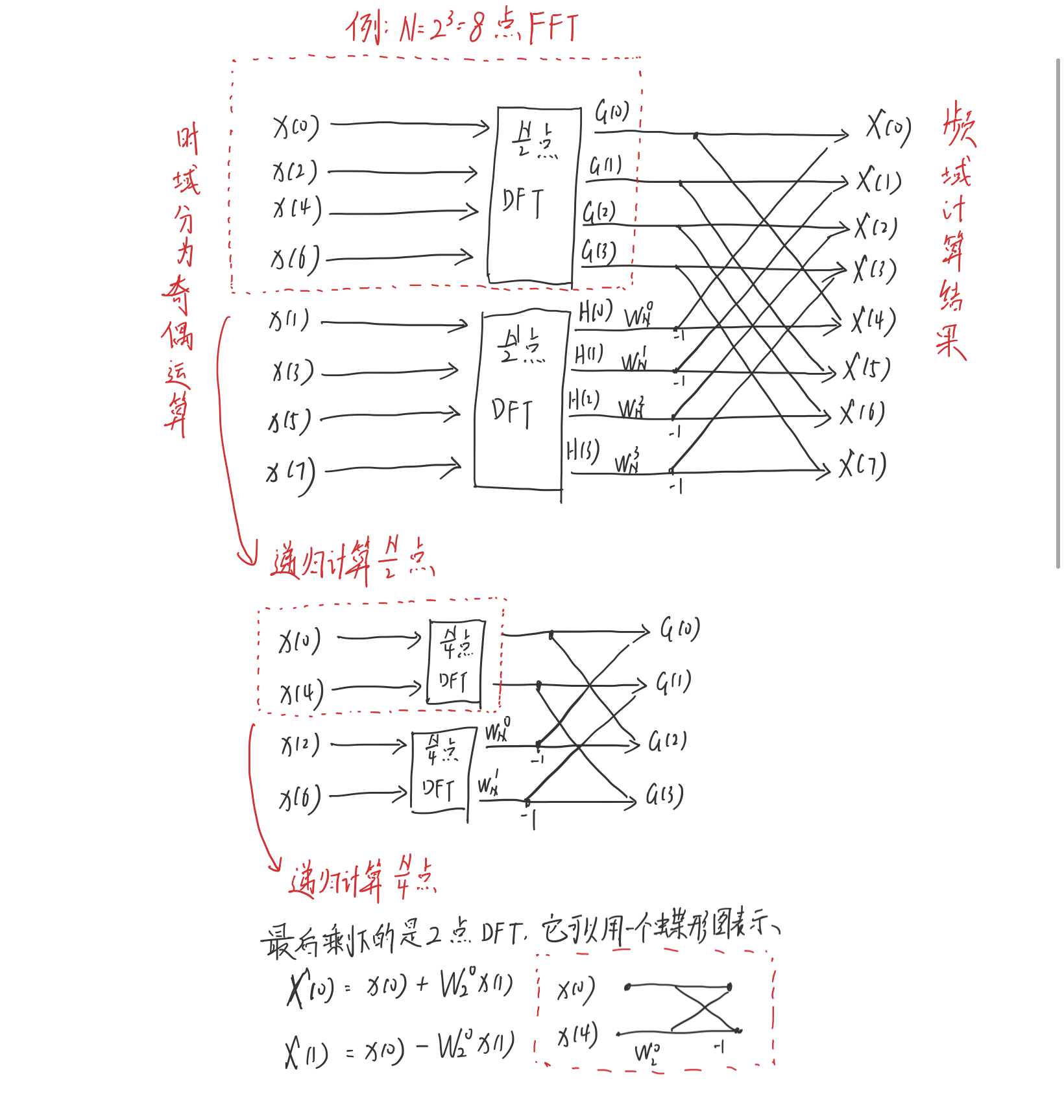
二：FFT的C++实现

#include <iostream> // fft算法实现，基2时间抽取
#include <vector>
#include <ctime>
using namespace std;

const double PI = acos(-1); // pi值

struct Cpx // 定义一个复数结构体和复数运算法则
{
	double r, i;
	Cpx() : r(0), i(0) {}
	Cpx(double _r, double _i) : r(_r), i(_i) {}
};
Cpx operator + (Cpx a, Cpx b) { return Cpx(a.r + b.r, a.i + b.i); }
Cpx operator - (Cpx a, Cpx b) { return Cpx(a.r - b.r, a.i - b.i); }
Cpx operator * (Cpx a, Cpx b) { return Cpx(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r); }

void fft(vector<Cpx>& a, int lim, int opt)
{
	if (lim == 1) return;
	vector<Cpx> a0(lim >> 1), a1(lim >> 1); // 初始化一半大小，存放偶数和奇数部分
	for (int i = 0; i < lim; i += 2)
		a0[i >> 1] = a[i], a1[i >> 1] = a[i + 1]; // 分成偶数部分和奇数部分

	fft(a0, lim >> 1, opt); // 递归计算偶数部分
	fft(a1, lim >> 1, opt); // 递归计算偶数部分

	Cpx wn(cos(2 * PI / lim), opt * -sin(2 * PI / lim)); //等于WN
	Cpx w(1, 0);
	for (int k = 0; k < (lim >> 1); k++) // 见蝶形图1运算过程
	{
		a[k] = a0[k] + w * a1[k];
		a[k + (lim >> 1)] = a0[k] - w * a1[k];
		w = w * wn;
	}

	//for (int k = 0; k < (lim >> 1); k++) // 见蝶形图2，小优化一下，少一次乘法
	//{
	//	Cpx t = w * a1[k];
	//	a[k] = a0[k] + t;
	//	a[k + (lim >> 1)] = a0[k] - t;
	//	w = w * wn;
	//}

}

int main()
{
	int opt = 1; // 1为FFT，-1为IFFT
	vector<Cpx> a(16); // 这里固定为16点，可以改变
	for (int i = 0; i < 16; i++) // 随机生成16个数作为待处理的数据
	{
		Cpx c = Cpx(cos(0.2 * PI * i), 0);
		a[i] = c;
	}

	if (1 == opt)
		fft(a, 16, opt); // a数组成为FFT过后的值
	else if (-1 == opt)
	{
		fft(a, 16, opt); // a数组成为IFFT过后的值
		for (int i = 0; i < 512; i++) a[i].r /= 512, a[i].i /= -512;// IFFT要除以长度
	}
	else;

	return 0;
}

---

三：MATLAB与C++混合编程

在工程上有的时候为了使数据处理更快或者支持某些定点运算，而选择将某些处理步骤用C/C++来处理，其实一般工程用MATLAB处理速度已经足够了，混合编程也全当是复习一下C++吧。

MATLAB与C++混合编程分为MATLAB中调用C++和C++中调用MATLAB，这里我们讨论的是前者。MATLAB与C++混合编程不是简单的把两种语言写在一起就行，而是需要遵循一种接口规范，具体在3.2中讨论。

3.1 混合编程步骤

从MATLAB的编译器配置到最后程序跳转到VS中打断点调试，在整个混合编程的过程中遇到了不少的困难，网上能找的资料多但是也杂乱，这里总结一下我从开始到最后所做的步骤。

① 我是用的是MATLAB2019b和VS2019，之前用的MATLAB2016，然后下载什么2019支持文件，修改注册表等等搞了很久也没弄好，索性直接换MATLAB2019b。

② MATLAB中运行mex -setup C++与mbuild -setup C++，如果不成功那就是当前版本的MATLAB不支持当前版本的Visual Studio，建议把MATLAB版本升高。不建议把VS的版本降低，会有兼容问题。

③ 不需要创建工程，直接创建一个xx.cpp文件按照mex接口定义写一个C++程序（具体程序之后讨论）。之前创建工程捣鼓了很久VS里面的配置问题，比如链接extern库等等，但感觉最后也并不需要创建工程，所以并不需要配置这些外部链接库？直接写xx.cpp文件就好了？（我也不太确定，也可能有用）

④ 程序写好之后在MATLAB中运行mex -g xx.cpp，如果xx.cpp程序写的符合规范的话，就会mex成功，生成xx.mexw64和xx.pdb文件；如果mex失败的话根据MATLAB返回的警告去修改代码。注意为了之后能进入到VS2019里断点调试，要加-g。

⑤ 在MATLAB脚本中写相应的测试程序，设置断点运行停在xx()函数处。

⑥ 用VS2019打开xx.cpp文件，在‘调试’一栏找到‘添加到进程’，进去 选择‘本机’，然后把MATLAB添加到进程。在你想停的地方设置断点。

⑦ MATLAB继续运行，则进入到VS2019中的相应断点处。（最后两步有可能进不去，其实我也是有时候能进去有时候不能，暂时也没有什么好的解决办法）

3.2 接口使用

mex文件是MATLAB中.m文件与VS中.cpp文件的桥梁，mex接口好坏关系到我们的MATLAB数据能不能正确地在C++程序中运行。

其中最重要的头文件和接口主函数如下，写法是固定的。

#include "mex.h"

void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])

int nrhs：输入参数的个数

mxArray *prhs[]:输入参数的指针数组

int nlhs：输出参数的个数

const mxArray *plhs[]：输出参数的指针数组

注意输入和输出都是以指针的形式传输的，可以理解成MATLAB把它的参数放到了某个地址处，然后C++中根据这个参数的长度去相应地址处读取相应长度的数据，就完成了参数的传递过程。相反最后再传递回去。

下面总结几个常用的mex函数：

读取参数时会用到的函数：

// 复数单值读取
double Nr1 = *mxGetPr(prhs[0]); // 读取第一个参数的实部
double Ni2 = *mxGetPr(prhs[1]); // 读取第二个参数的虚部

// 地址读取
double* Pr1 = mxGetPr(prhs[0]); // 读取第一个参数的实部地址
double* Pi2 = mxGetPi(prhs[0]); // 读取第一个参数的虚部地址

// 矩阵维度读取
int M = mxGetM(prhs[2]); // 读取第三个参数的行数
int N = mxGetN(prhs[2]); // 读取第三个参数的列数

待补充

输出参数时会用到的函数：

// 输出复矩阵
plhs[0] = mxCreateDoubleMatrix(M, N, mxCOMPLEX); // 创建M*N的复矩阵
double* outPr = mxGetPr(plhs[0]);
double* outPi = mxGetPi(plhs[0]);

待补充

3.3 FFT的MATLAB/C++混合实现

先将第二章中FFT的代码用mex接口改写成如下形式：

# include "mex.h"
# include <vector>
# include <ctime>

const double PI = acos(-1); // pi

struct Cpx // 定义一个复数结构体和复数运算法则
{
	double r, i;
	Cpx() : r(0), i(0) {}
	Cpx(double _r, double _i) : r(_r), i(_i) {}
};
Cpx operator + (Cpx a, Cpx b) { return Cpx(a.r + b.r, a.i + b.i); }
Cpx operator - (Cpx a, Cpx b) { return Cpx(a.r - b.r, a.i - b.i); }
Cpx operator * (Cpx a, Cpx b) { return Cpx(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r); }

void fft(std::vector<Cpx>& a, int lim, int opt)
{
	if (lim == 1) return;
	std::vector<Cpx> a0(lim >> 1), a1(lim >> 1);
	for (int i = 0; i < lim; i += 2)
		a0[i >> 1] = a[i], a1[i >> 1] = a[i + 1]; // 分成偶数部分和奇数部分

	fft(a0, lim >> 1, opt);
	fft(a1, lim >> 1, opt);

	Cpx wn(cos(2 * PI / lim), opt * -sin(2 * PI / lim));
	Cpx w(1, 0);
	for (int k = 0; k < (lim >> 1); k++) // 蝶形运算过程
	{
		a[k] = a0[k] + w * a1[k];
		a[k + (lim >> 1)] = a0[k] - w * a1[k];
		w = w * wn;
	}
}

void mexFunction(int nlhs, mxArray* plhs[], int nrhs, const mxArray* prhs[]) // mex主函数
{
	int M = mxGetM(prhs[0]); // 输入矩阵行数
	int N = mxGetN(prhs[0]); // 输入矩阵列数
	double* xpr = mxGetPr(prhs[0]); // 输入矩阵实部指针
	double* xpi = mxGetPi(prhs[0]); // 输入矩阵虚部指针
	int lim = *mxGetPr(prhs[1]); // 输入参数，长度，这里输入的为行向量，所以lim = N，M = 1
	int opt = *mxGetPr(prhs[2]); // 输入参数，选择， 1为FFT，-1为IFFT

	plhs[0] = mxCreateDoubleMatrix(M, N, mxCOMPLEX); // 输出矩阵创建（重要）
	double* ypr = mxGetPr(plhs[0]); // 输出矩阵实部指针
	double* ypi = mxGetPi(plhs[0]); // 输出矩阵虚部指针

	std::vector<Cpx> a(lim); // 用vector存储数据
	for (int i = 0; i < lim; i++) // 输入向量传入
	{
		a[i].r = xpr[i];
		a[i].i = xpi[i];
	}

	if (1 == opt)
		fft(a, lim, opt); // a数组变为FFT过后的值
	else if (-1 == opt)
	{
		fft(a, lim, opt); // a数组变为IFFT过后的值
		for (int i = 0; i < lim; i++) a[i].r /= lim, a[i].i /= lim;// IFFT要除以长度
	}
	else;

	for (int i = 0; i < lim; i++) // 输出向量传出
	{
		ypr[i] = a[i].r;
		ypi[i] = a[i].i;
	}

	return;
}

再在MATLAB脚本中写如下程序：

clear all
mex fftxx.cpp -g
a = randn(1, 16) + 1i * randn(1, 16); % 随机生成16个复数数据
fftsize = 16;
b = fftxx(a, fftsize, 1)   % 传入C++中进行FFT处理
b1 = fft(a,fftsize)         % MATLAB系统函数进行FFT处理

c = fftxx(b, fftsize, -1)  % 传入C++中进行IFFT处理
c1 = ifft(b, fftsize)       % MATLAB系统函数进行IFFT处理

最后运行该.m程序，在MATLAB命令行窗口中可以看到b和b1，c和c1输出结果完全一致。