Why系统：0.1 + 0.2 != 0.3

为了知道更多一点，打算自己来一个why系列。

面试官：同学，请问 0.1 + 0.2 等于多少
同学：不等于0.3，因为精度问题
面试官：能更深入的说一下嘛
同学：......

上面的同学，就是曾今的我！

所以，干！

来解决 0.1 + 0.2 这个小学生都会的题目，大致分三个步骤

进制转换

十进制转二进制
二进制转十进制

IEEE 754浮点数标准
浮点数计算
0.1 + 0.2

进制转换

十进制转二进制

整数：采用 除2取余，逆序排列法。具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
小数：采用乘2取整，顺序排列法。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。

我们依旧使用 9.375 来分析，

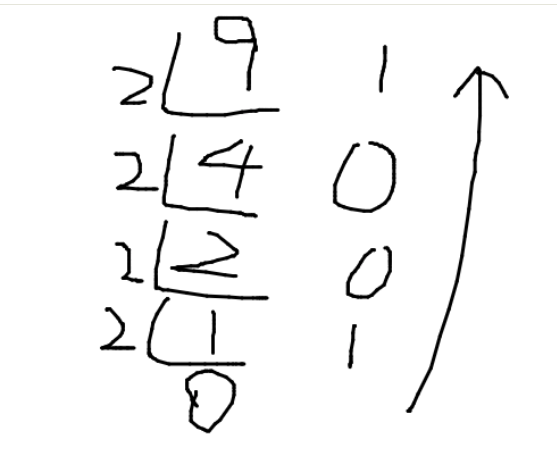
先看整数部分：9, 按照规则，除2取余，逆序排列，

结果为： 1001

再看小数部分： 0.375 ,按照规则 采用乘2取整，顺序排列

结果为： 011

结合起来 9.375 = 整数₂ + 小数₂ = 1001 + .011 = 1001.011

验证：

(9.375).toString(2)  // 1001.011

Number.prototype.toString.call(9.375, 2)  // 1001.011

Number.prototype.toString.call( Number(9.375), 2) // 1001.011

二进制转十进制

小数点前或者整数要从右到左用二进制的每个数去乘以2的相应次方并递增
小数点后则是从左往右乘以二的相应负次方并递减。

例如：二进制数1001.011转化成十进制

整数部分：1001 = 1 * 2⁰ + 0 * 2¹ + 0 * 2² + 1 * 2³ = 1 + 0 + 0 + 8 = 9

小数部分：011 = 0 * 2^-1 + 1 * 2^-2 + + 1 * 2^-3 = 0 + 0.25 + 0.125 = 0.375

1001.011₂ = 整数部分 + 小数部分 = 9₁₀ + 0.375 ₁₀ = 9.375

当然我们怎么验证结果了，调用Number.prototype.toString

(9.375).toString(2)  // 1001.011

Number.prototype.toString.call(9.375, 2)  // 1001.011

Number.prototype.toString.call( Number(9.375), 2) // 1001.011

IEEE 754浮点数标准

以双精度浮点格式为例，如上图，三个参数 S E M:

名称                        长度        比特位置

符号位    Sign  （S）      : 1bit        （b63）

指数部分Exponent （E）     : 11bit      （b62-b52）

尾数部分Mantissa   （M）   : 52bit      （b51-b0）

双精度的指数部分（E）采用的偏置码为1023

S=1表示负数 S=0表示正数

求值公式 (-1)^S*(1.M)*2^(E-1023)

这里有一个额外的参数，偏移码 1023，更多可以参考IEEE 754浮点数标准中64位浮点数为什么指数偏移量是1023

结合公司来看，各个参数是怎么工作的：

二进制可能不好理解，我们先看一个10进制的数，比如 1001.125, 我们可以写成

1001.125
100.1125*10¹
10.01125*10²
1.001125*10³

上面的(-1)^S*(1.M)*2^(E-1023) 同 1.001125*10³ 只不过使用的是二进制而已。

如果是小数了，同理 0.0000125 就是 1.25 * 10^-5

我们来看看一个二进制的例子，比如 103.0625

S 符号位

因为正数，所以 S为0
E 指数位
1. 转为二进制为 1100111.0001
2. 规范化 1.1001110001 * 2⁶, 6 = E - 1023 , E = 1029
3. E = 1029 , 转为二进制 10000000101
M 尾数位

对于 1.1001110001 ， M的值为 1001110001, 因为长度有52位，后面补充0就行，结果为

1001110001000000000000000000000000000000000000000000

拼接来 0-10000000101-1001110001000000000000000000000000000000000000000000

至于如何验证对不对，可以去IEEE 754 64位转换工具验证一下。

大家知道，十进制有无限循坏小数，二进制也是存在的。遇到这种情况，10进制是四舍五入，那二进制呢。只有0和1，那么是1就入吧。

当然 IEEE 754 是有好几种舍入误差的模式的，更多细节可以阅读 IEEE 754浮点数标准详解。

我们看看 1.1, 最后尾数部分 0001100110011001100110011001100110011001100110011001₅₂ (11001)_循环，53位是1，那就进位吧，

结果为 0001100110011001100110011001100110011001100110011010

这里知道十进制，怎么转换为二进制的浮点数存储了，下面就可以进行运算。

浮点数计算

浮点数的加减运算一般由以下五个步骤完成：对阶、尾数运算、规格化、舍入处理、溢出判断。更多细节，可以阅读浮点数的运算步骤。

1.对阶

这里的阶，就是指数位数，简单说，就是指数位保持一致。即⊿E＝E x-E y，将小阶码加上⊿E，使之与大阶码相等。

拿是十进制举例， 123.5 + 1426.00456

等价于 1.235*10² + 1.42600456 * 10³
和指数高的对齐，高的为3 ，变成 0.1235*10³ + 1.42600456 * 10³

123.5 + 1426.00456 = 0.1235*10³ + 1.42600456 * 10³ = (0.125 + 1.42600456) * 10³ = 1.54950456 * 10³ = 1549.50456

举例是十进制，计算机执行的是二进制而已。这个过程可能会有几个问题。

小阶对大阶的时候，会右移动，因为指数部分，最多保留52位，就可能丢。
相加或者相减，值可能溢出，就有了后面的溢出判断。

2.尾数运算

尾数运算就是进行完成对阶后的尾数相加减。

3.结果规格化

在机器中，为保证浮点数表示的唯一性，浮点数在机器中都是以规格化形式存储的。对于IEEE754标准的浮点数来说，就是尾数必须是1.M的形式。

再拿十进制举例。

80.5 + 90 = 8.05*10¹ + 9.0*10¹ = 17.05¹

尾数必须是1.M的形式，规格化 => 1.705 ²

4.舍入处理

浮点运算在对阶或右规时，尾数需要右移，被右移出去的位会被丢掉，从而造成运算结果精度的损失。为了减少这种精度损失，可以将一定位数的移出位先保留起来，称为保护位，在规格化后用于舍入处理。

IEEE754标准列出了四种可选的舍入处理方法，默认使用四舍五入。

5.溢出判断

与定点数运算不同的是，浮点数的溢出是以其运算结果的阶码的值是否产生溢出来判断的。

若阶码的值超过了阶码所能表示的最大正数，则为上溢，进一步，若此时浮点数为正数，则为正上溢，记为+∞，若浮点数为负数，则为负上溢，记为-∞；若阶码的值超过了阶码所能表示的最小负数，则为下溢，进一步，若此时浮点数为正数，则为正下溢，若浮点数为负数，则为负下溢。正下溢和负下溢都作为0处理

0.1 + 0.2 != 0.3

换算成 IEEE 754 标准的二进制数据结构

在如上基础之类，我们再开始我们的议题0.1 + 0.2 != 0.3, 计算机首先会把十进制转为二进制，然后进行加法。

0.1 转二进制为, 终止条件是 直到积中的小数部分为零，但是从下面的结果来看, 所以简单表示为

0.0 0011 0011 (0011)_无限循环，无限循环，这可不行，这次轮到 IEEE 754标准 出场了，IEEE 754标准定义了单精度和双精度浮点格式

2 * 0.1

2 * 0.2        0

2 * 0.4        0

2 * 0.8        0

2 * 1.6        1

2 * 1.2        1

2 * 0.4        0

2 * 0.8        0

2 * 1.6        1

2 * 1.2        1

2 * 0.4        0

2 * 0.8        0

2 * 1.6        1

2 * 1.2        1

.....无限循环0011....

我们以0.1为例，开始计算

符号位S

因为是正数，那么符号位为 0 。
指数部分E

首先我们将0.1转为2进制数0.0 0011 0011 (0011)_无限循环，因为是正数，那么符号位为 0。然后我们根据正规化的二进制浮点数表达，那么它以1.bbbbb...这种形式表示, 为：1.1001 1001 (1001)_无限循环 x 2^-4。

E-1023 = -4 那么 E = 1019, 1019的二进制表示为 1111111011, 因为有11位，前面加0，为01111111011
尾数部分M, 无限循环

1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001_无限循环

当64bit的存储空间无法存储完整的无限循环小数，而IEEE 754 Floating-point采用round to nearest, tie to even的舍入模式。

1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 ~~1001~~ 就进位为

1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1010

最终

0-01111111011-1001100110011001100110011001100110011001100110011010

你也可使用 IEEE 754 64位转换工具来验证自己的结果是否正确。

同理0.2的最终结果为

0-01111111100-1001100110011001100110011001100110011001100110011010

接下来，进行标准的浮点数运算

对阶

小阶对大阶。

0.1 的指数 01111111011 = 1019

0.2 的指数 01111111100 = 1020

0.2 的指数大，0.1的调整指数位为 01111111100，同时位数部分右移一位，如下：

0.1    0-01111111100-11001100110011001100110011001100110011001100110011010

0.2    0-01111111100-1001100110011001100110011001100110011001100110011010

尾数运算

可以看到有进位

    0.11001100110011001100110011001100110011001100110011010    ---0.1尾数

    1.1001100110011001100110011001100110011001100110011010     ---0.2尾数

-----------------------------------------------------------------------------

   10.01100110011001100110011001100110011001100110011001110     

         结果

结果规格化

需要右移一位， E+1 = 1020 + 1 = 1021 = 1111111101

1.M = 1.001100110011001100110011001100110011001100110011001110

舍入处理

尾数小数部分 0011001100110011001100110011001100110011001100110011 10 长度为54，

四舍五入 0011001100110011001100110011001100110011001100110100

溢出检查

指数没有溢出

结果计算：：

E 为 1021, S为0

计算值： (-1)^S*(1.M)*2^(E-1023) => (1.0011001100110011001100110011001100110011001100110100)*2^(-2)

=> 0.010011001100110011001100110011001100110011001100110100

通过在线进制转换, 结果为 0.30000000000000004。

话外

既然有这个问题，那么我们怎么老保证结果的正确性呢。

比如钱，明确的知道最多两位小数，那么不妨先 *100
与一个非常小的值对比。比如 Number.EPSILON

浮点数的运算步骤

 IEEE 754-维基百科

 IEEE 754浮点数标准详解

 JS魔法堂：彻底理解0.1 + 0.2 === 0.30000000000000004的背后

 IEEE 754 64位转换工具