最小生成树（Prim算法，Kruskal算法 ）

声明：图片及内容基于https://www.bilibili.com/video/BV1yp4y1Q74o?from=articleDetail

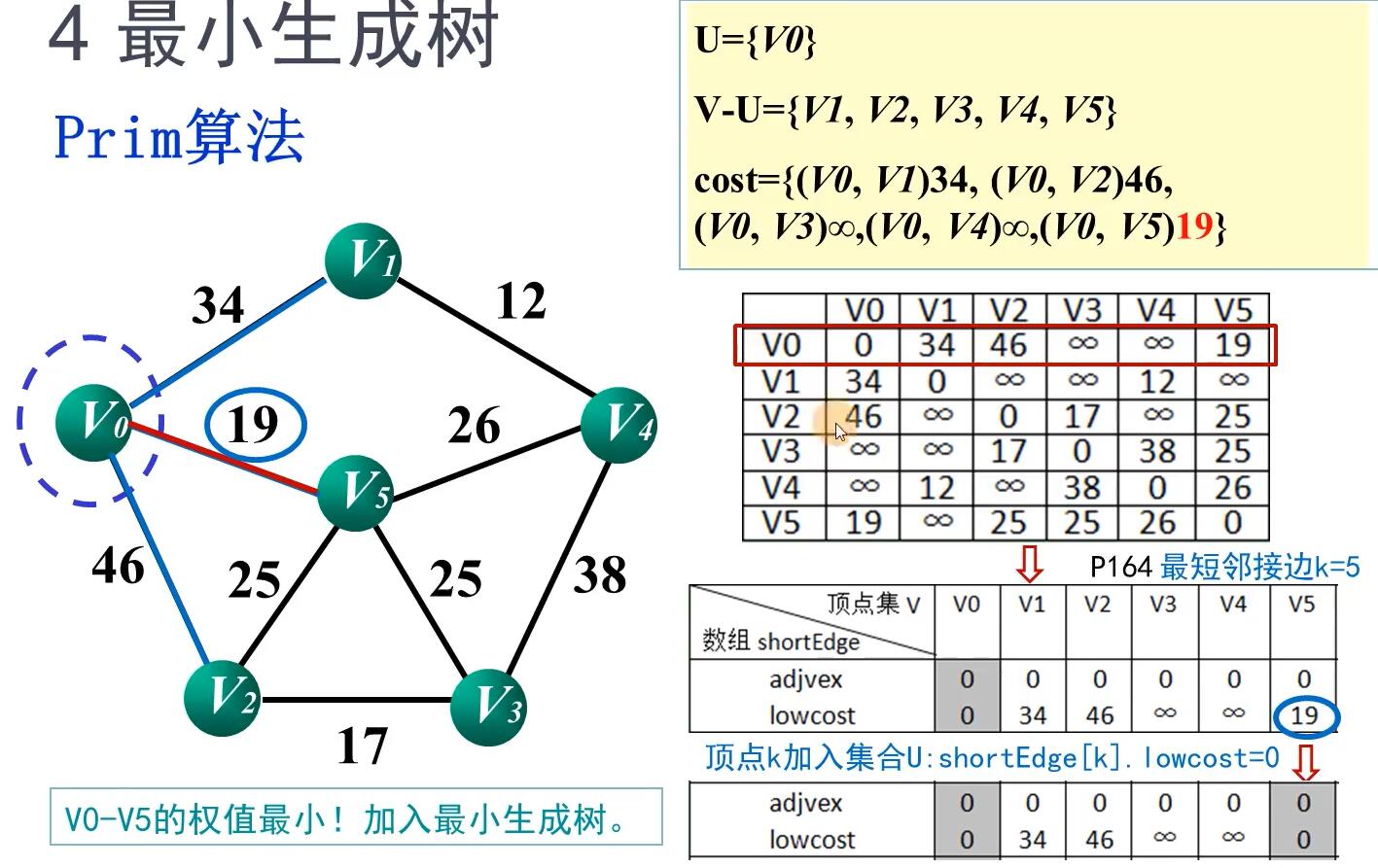
最小生成树原理

、

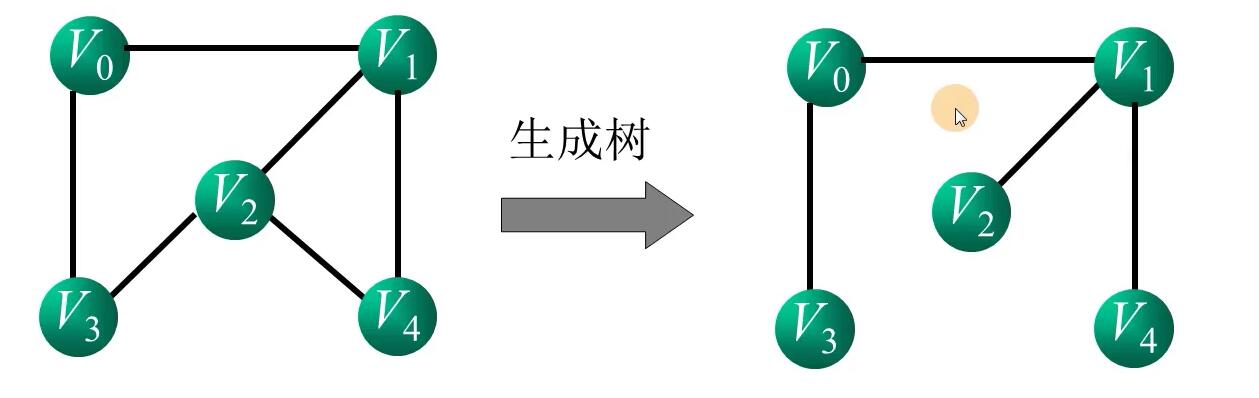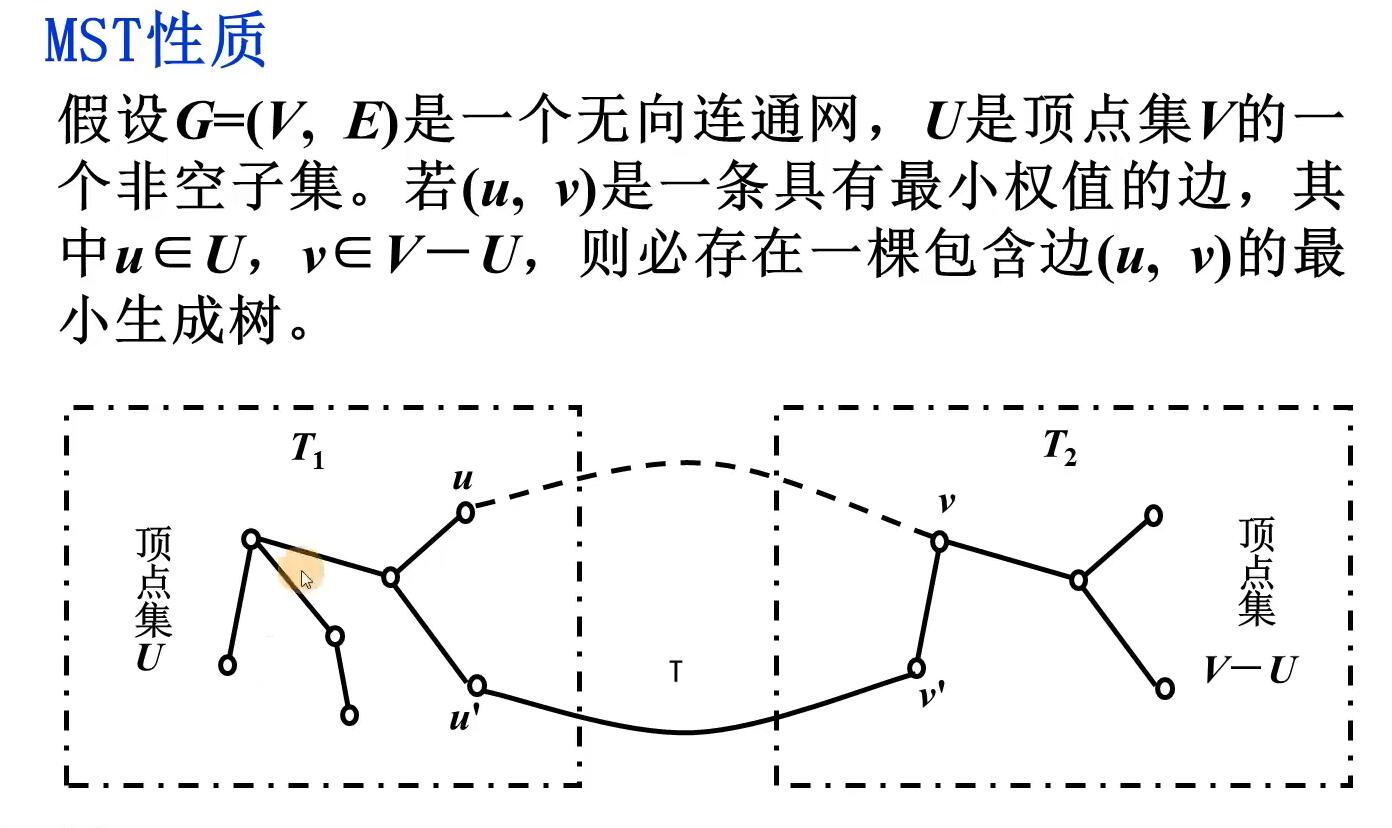
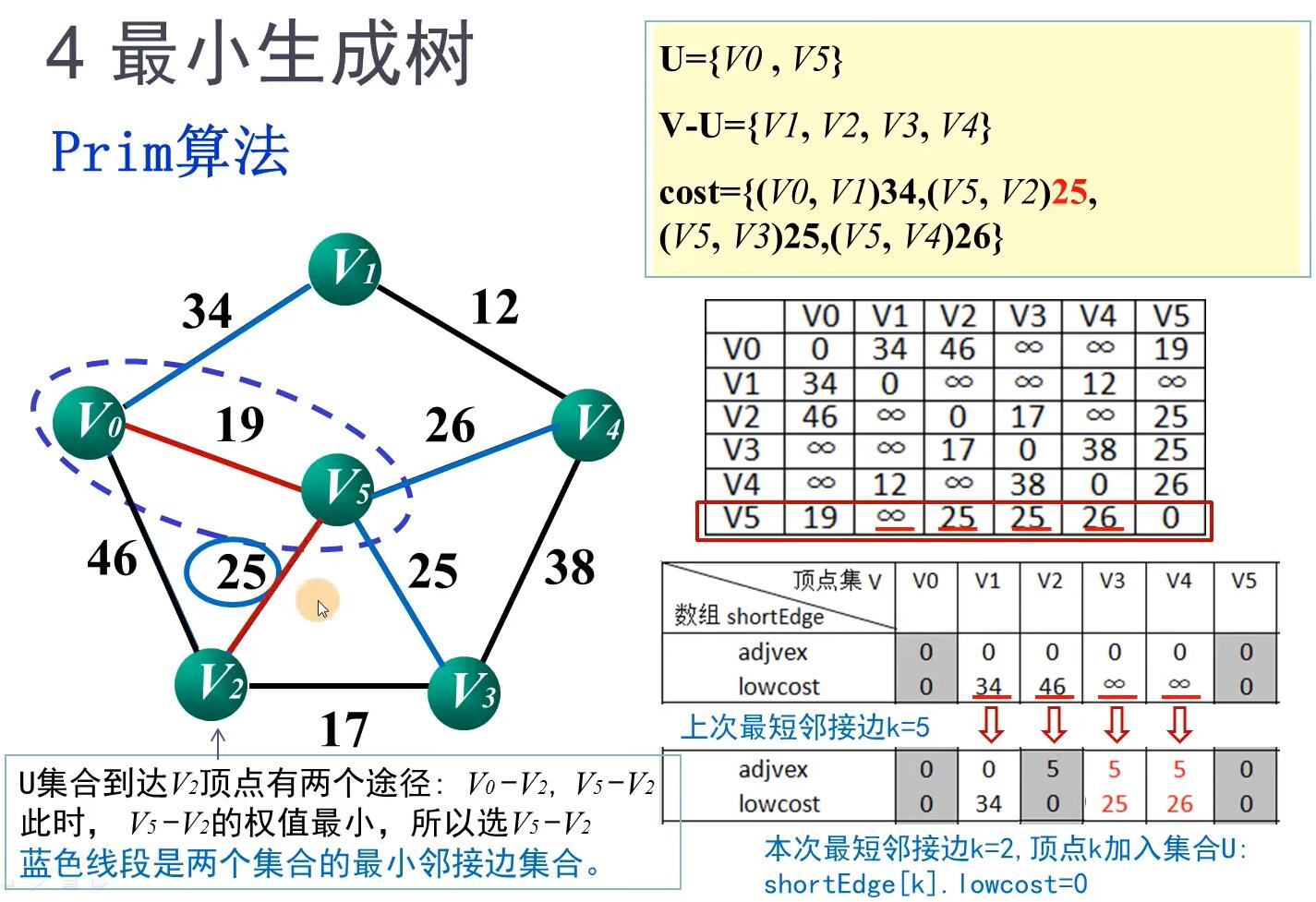
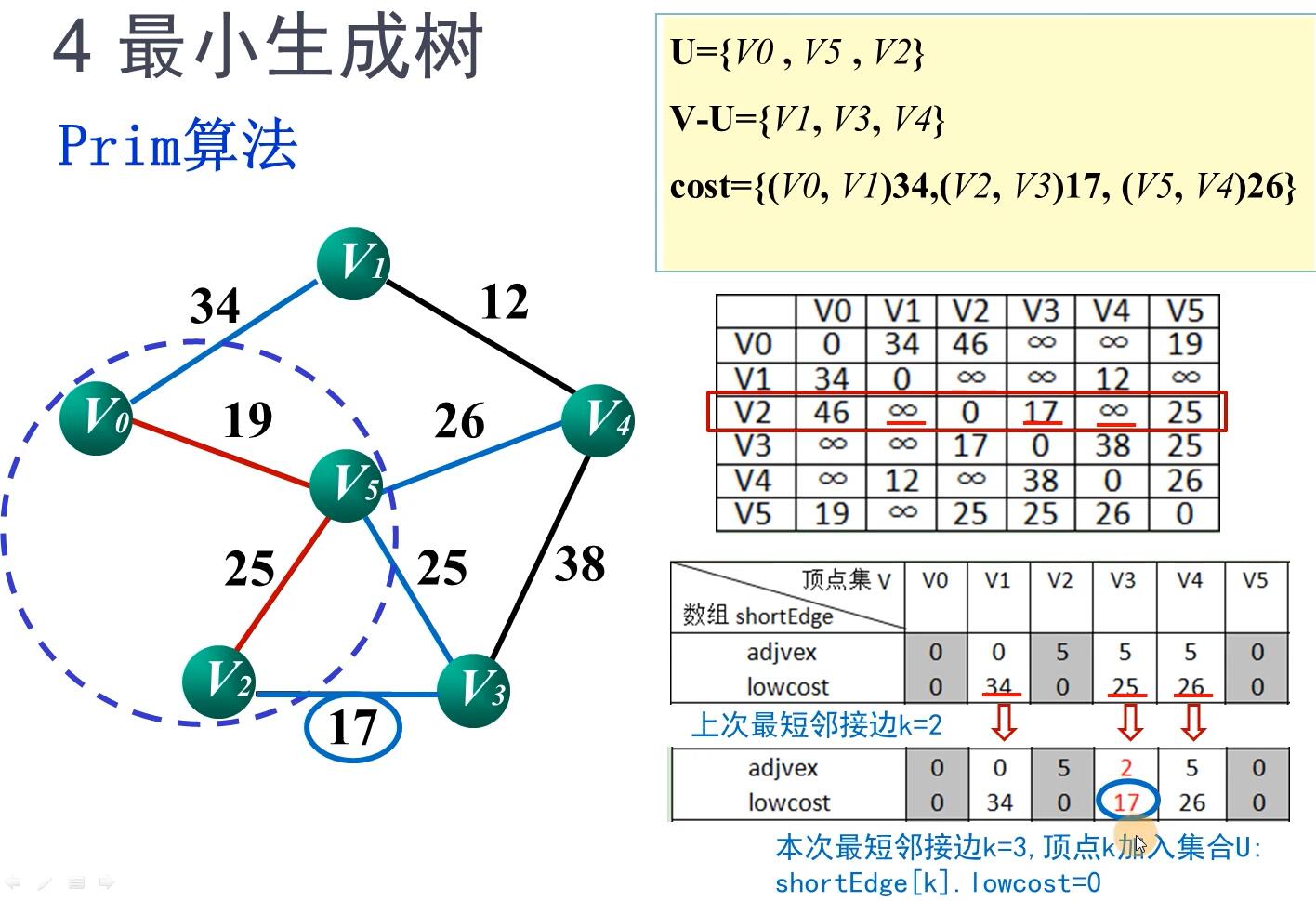
普利姆（Prim）算法

原理

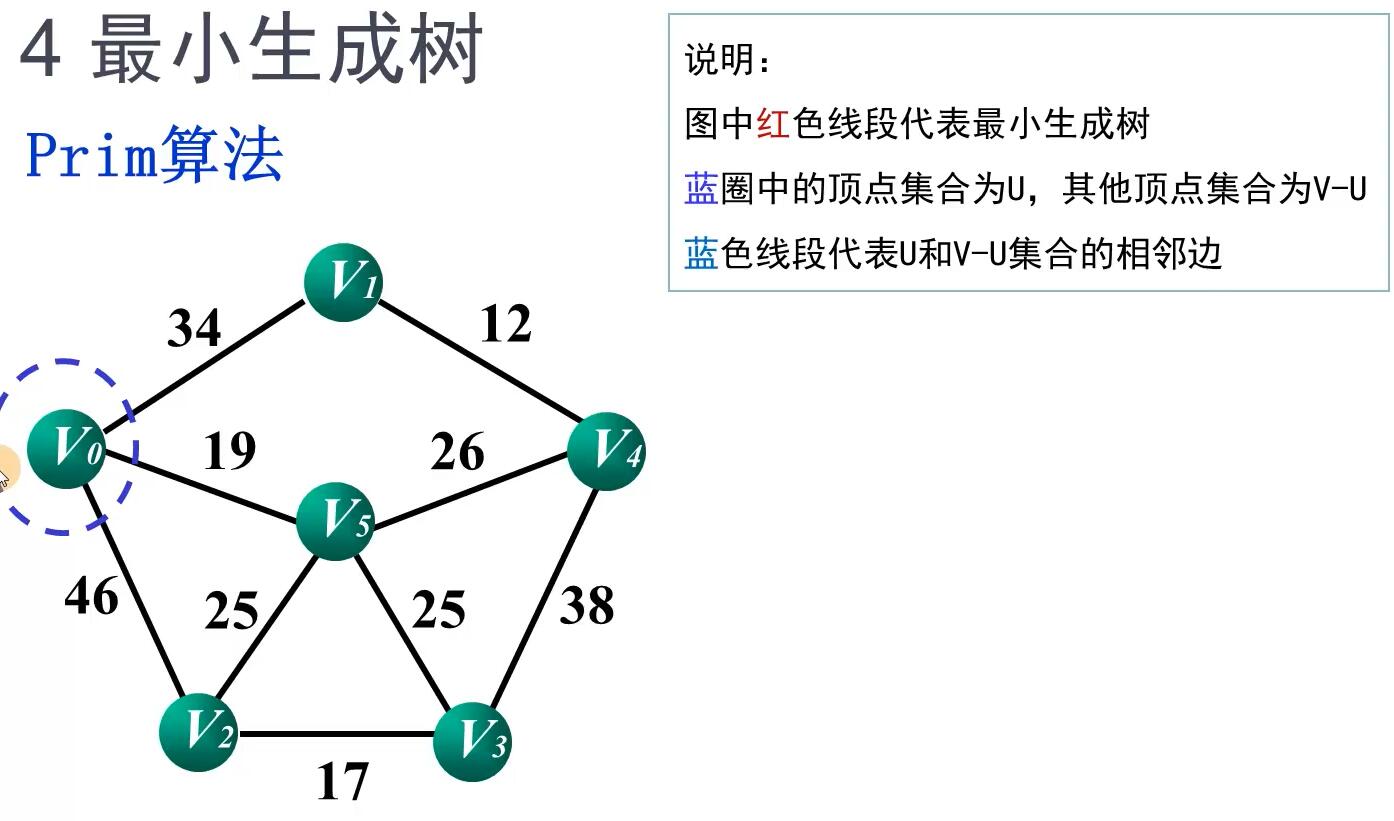
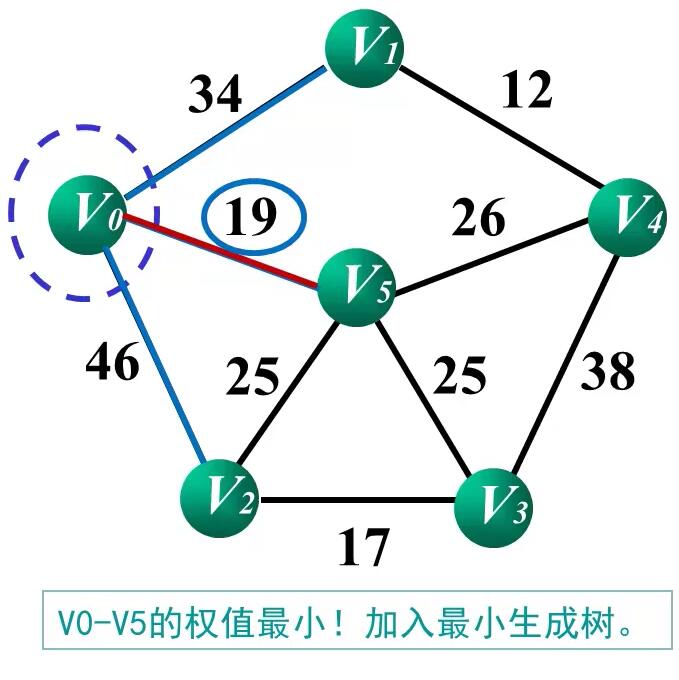
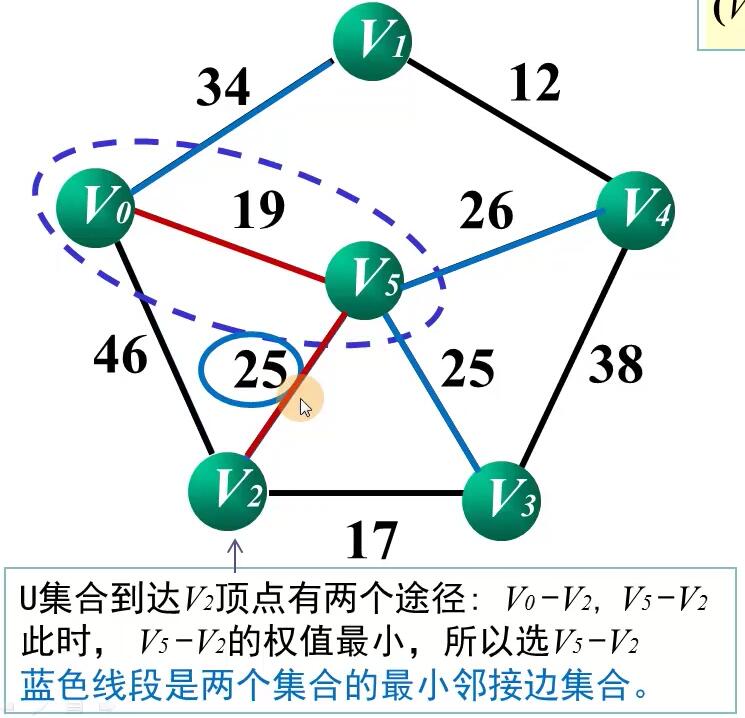
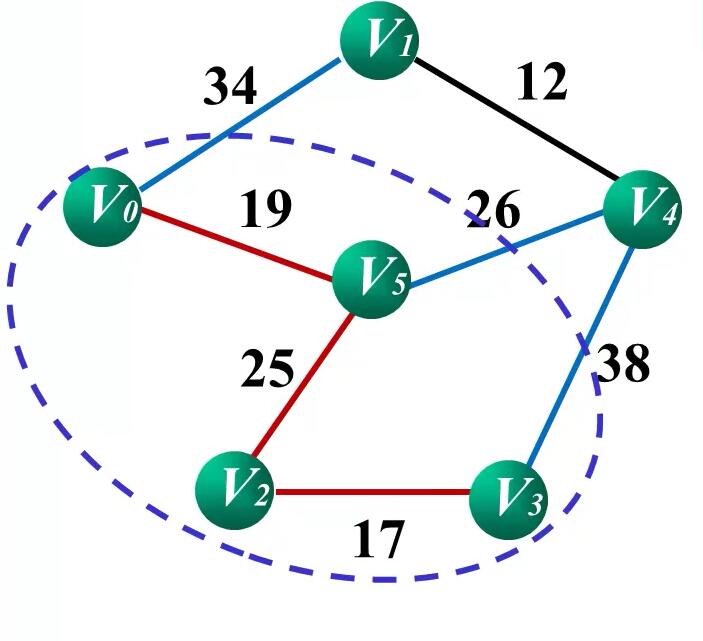
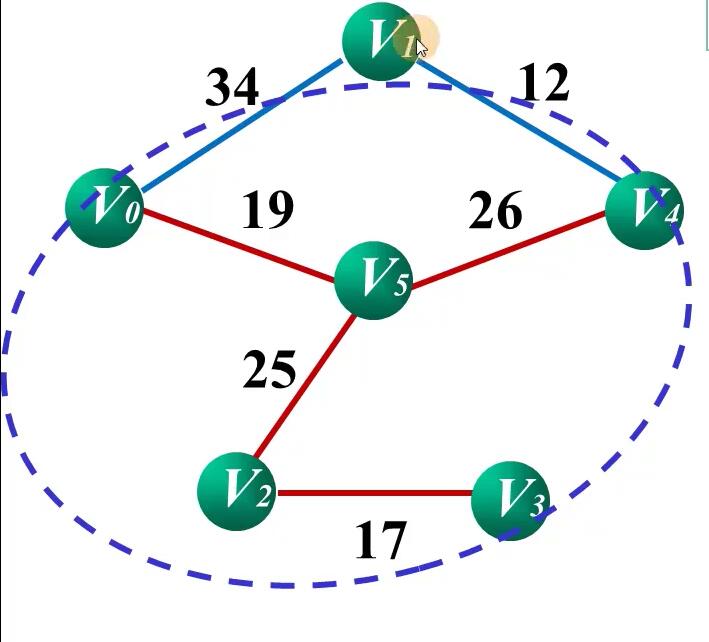
Prim算法的实现

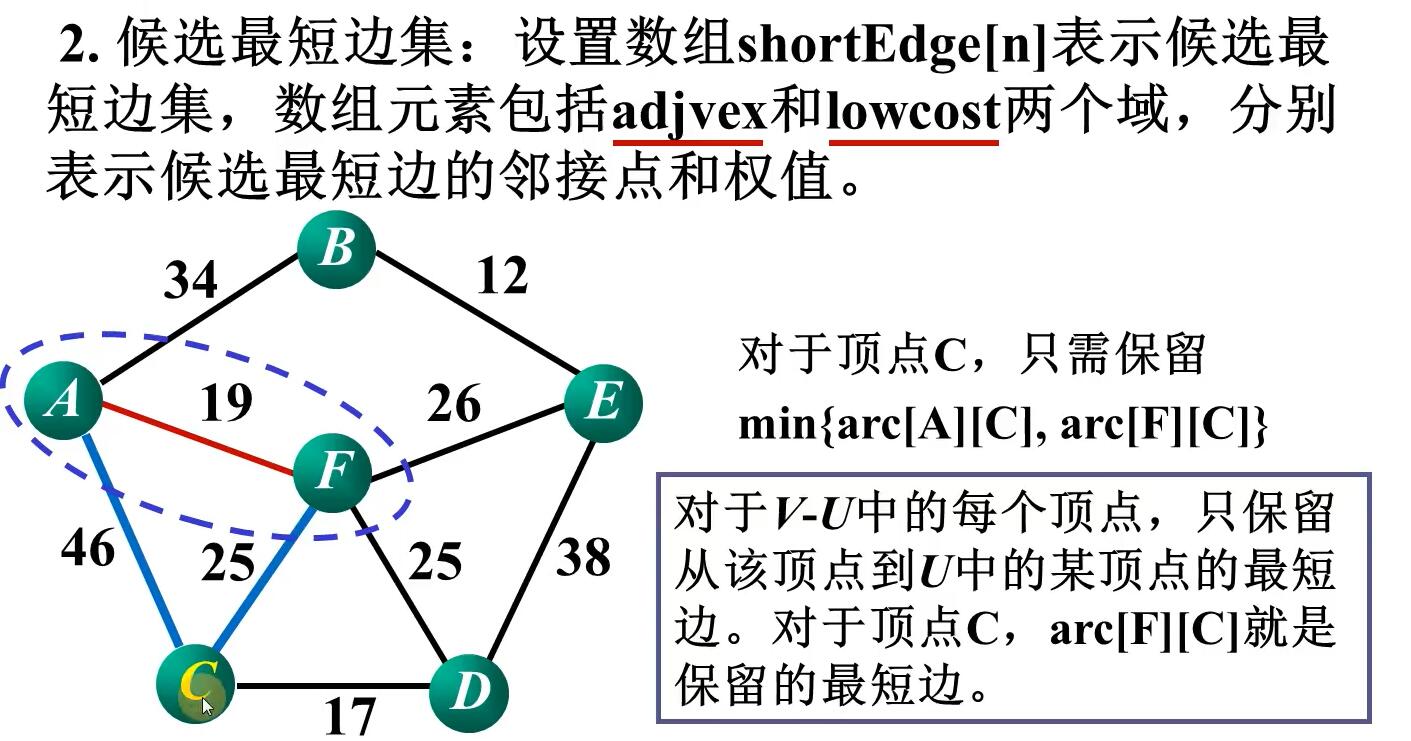
核心代码

void MGraph::Prim(int start){
    shortEdge shortEdge;                     //建立shortEdge数组
    for(int i=0;i<vertexNum;i++){
        shortEdge[i].lowcost=arc[start][i]; // 数组初始化，lowcost为邻接矩阵第i行的权值
        shortEdge[i].adjvex=start;          //adjvex初始化为起始值
    }
    shortEdge[start].lowcost=0;;            //lowcost为0，把start放入集合 

    for(int i=0;i<vertexNum;i++){
        int k=minEdge(shortEdge,vertexNum); //求出最小权值下标
        if(k==-1) return ;                  //shortEdge的lowcost都为0，及所有结点都在集合中，算法结束
        outputSMT(k,shortEdge[k]);
        shortEdge[k].lowcost=0;             //k放入集合
        for(int j=0;j<vertexNum;j++){           //更新shortEdge数组，当前集合和刚进入集合的结点的权值比较
            if(arc[k][j]<shortEdge[j].lowcost){
                shortEdge[j].lowcost=arc[k][j];
                shortEdge[j].adjvex=k;
            }
        }
    }
}

int minEdge(shortEdge shortEdge,int vertexNum){  //求shortEdge数组中最小权值的下标
    Edge e;                   //e是个临时变量用来记录当前小权值的下标和权值
    e.lowcost=INFINIT;
    e.adjvex=-1;
    int i;
    for(i=0;i<vertexNum;i++){             //权值不为0（已经在集合中），不为无穷 （无路径）
        if(shortEdge[i].lowcost!=0&&shortEdge[i].lowcost!=INFINIT&&e.lowcost>shortEdge[i].lowcost){
            e.lowcost=shortEdge[i].lowcost;
            e.adjvex=i;
        }

    }
    return e.adjvex;
}

void outputSMT(int k,Edge Edge){            //打印路径和权值
    cout<<"("<<Edge.adjvex<<","<<k<<") "<<Edge.lowcost<<endl;
}

完整代码

#include<iostream>
#define MAXVEX 100
using namespace std;
const int INFINIT=65535;
int visit[MAXVEX];
typedef struct Edge{
    int lowcost;
    int adjvex;
}Edge,shortEdge[MAXVEX];

class MGraph {
    private:
        int *vertex;         //顶点信息
        int **arc;         //邻接矩阵
        int vertexNum,arcNum;        //顶点数，边数
    public:
        MGraph(int v[],int n,int e);
        ~MGraph();
        void display();
        void Prim(int start);
};

MGraph::MGraph(int v[],int n,int e) {  //n是顶点数，e是边数
    vertexNum=n;
    arcNum=e;
    vertex = new int[vertexNum];         //建立顶点信息
    arc = new int*[vertexNum];         //建立邻接表
    for(int i=0; i<vertexNum; i++)
        arc[i]=new int[vertexNum];

    for(int i=0; i<vertexNum; i++) {   //初始化顶点信息
        vertex[i]=v[i];
    }
    for(int i=0;i<vertexNum;i++)       //初始化邻接表
        for(int j=0;j<vertexNum;j++){
            if(i==j)     arc[i][j]=0;
            else     arc[i][j]=INFINIT;
        }

    int vi,vj,w;
    for(int i=0;i<arcNum;i++){
        cout<<"请输入边的两个顶点和这条边的权值"<<endl;
        cin>>vi>>vj>>w;   //输入边依附的两个顶点的编号 和权值
        arc[vi][vj]=w; //有边标志
        arc[vj][vi]=w;
    }
}

void MGraph::display(){
    for(int i=0;i<vertexNum;i++){
        for(int j=0;j<vertexNum;j++){
            if(arc[i][j]==INFINIT)
                cout<<"∞"<<"\t";
            else cout<<arc[i][j]<<"\t";
        }
        cout<<endl;
    }
    cout<<endl;

    for(int i=0;i<vertexNum;i++){
        cout<<vertex[i]<<" ";
    }
    cout<<endl;
}

MGraph::~MGraph(){
    delete []vertex;
    for(int i=0;i<vertexNum;i++)
        delete [] arc[i];
    delete [] arc;
}
int minEdge(shortEdge shortEdge,int vertexNum){  //求shortEdge数组中最小权值的下标
    Edge e;                   //e是个临时变量用来记录当前小权值的下标和权值
    e.lowcost=INFINIT;
    e.adjvex=-1;
    int i;
    for(i=0;i<vertexNum;i++){             //权值不为0（已经在集合中），不为无穷 （无路径）
        if(shortEdge[i].lowcost!=0&&shortEdge[i].lowcost!=INFINIT&&e.lowcost>shortEdge[i].lowcost){
            e.lowcost=shortEdge[i].lowcost;
            e.adjvex=i;
        }

    }
    return e.adjvex;
}
void outputSMT(int k,Edge Edge){            //打印路径和权值
    cout<<"("<<Edge.adjvex<<","<<k<<") "<<Edge.lowcost<<endl;
}
void MGraph::Prim(int start){
    shortEdge shortEdge;                     //建立shortEdge数组
    for(int i=0;i<vertexNum;i++){
        shortEdge[i].lowcost=arc[start][i]; // 数组初始化，lowcost为邻接矩阵第i行的权值
        shortEdge[i].adjvex=start;          //adjvex初始化为起始值
    }
    shortEdge[start].lowcost=0;;            //lowcost为0，把start放入集合 

    for(int i=0;i<vertexNum;i++){
        int k=minEdge(shortEdge,vertexNum); //求出最小权值下标
        if(k==-1) return ;                  //shortEdge的lowcost都为0，及所有结点都在集合中，算法结束
        outputSMT(k,shortEdge[k]);
        shortEdge[k].lowcost=0;             //k放入集合
        for(int j=0;j<vertexNum;j++){           //更新shortEdge数组，当前集合和刚进入集合的结点的权值比较
            if(arc[k][j]<shortEdge[j].lowcost){
                shortEdge[j].lowcost=arc[k][j];
                shortEdge[j].adjvex=k;
            }
        }
    }
}

int main(){
    int v[6]={0,1,2,3,4,5};
    cout<<"请输入顶点个数和边的个数"<<endl;
    int m,n;
    cin>>m>>n;
    cout<<"请输入prim算法的起点"<<endl;
    int k;
    cin>>k;

    MGraph mgraph(v,m,n);
    cout<<"输出邻接矩阵信息和边数组信息："<<endl;
    mgraph.display();
    cout<<"输出起点从"<<k<<"开始的最小生成树：" <<endl;
    mgraph.Prim(k);
    return 0;
}

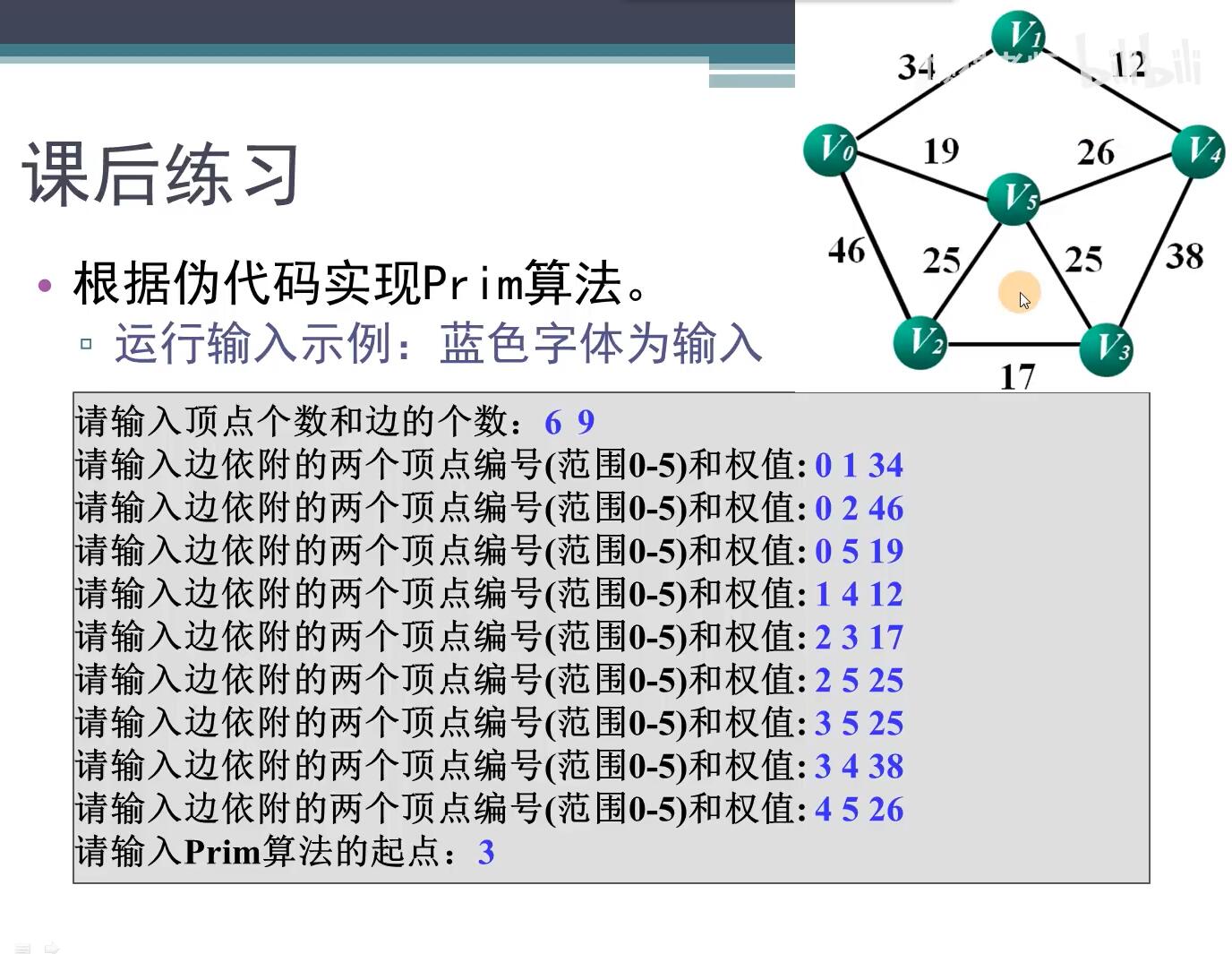
输入：

6 9

3

0 1 34
0 2 46
0 5 19
1 4 12
2 3 17
2 5 25
3 5 25
3 4 38
4 5 26

输出：

输出邻接矩阵信息和边数组信息：
0  34  46  ∞  ∞  19
34 0   ∞   ∞  12  ∞
46 ∞   0   17 ∞  25
∞  ∞   17  0  38 25
∞  12  ∞  38  0  26
19 ∞   25 25 26  0

0 1 2 3 4 5
输出起点从3开始的最小生成树：
(3,2) 17
(3,5) 25
(5,0) 19
(5,4) 26
(4,1) 12