AcWing 199. 余数之和

\(\sum_{i = 1}^{n} k \bmod i = n * k - \sum_{i = 1}^{n} \lfloor k / i \rfloor * i\)

显然，\(\lfloor k / i \rfloor\) 是最棘手的，我们要想办法简化计算。

证明单调性

• 观察 \(\lfloor k / i \rfloor\)，显然随着 \(i\) 的增大，这个式子是越来越小的。

• 又因为有向下取整符号，所以该式子取值只能是整数。

若我们设函数 \(f(x) = \lfloor k / x \rfloor\)。则画在坐标轴中应该是从高到低一条条横线。

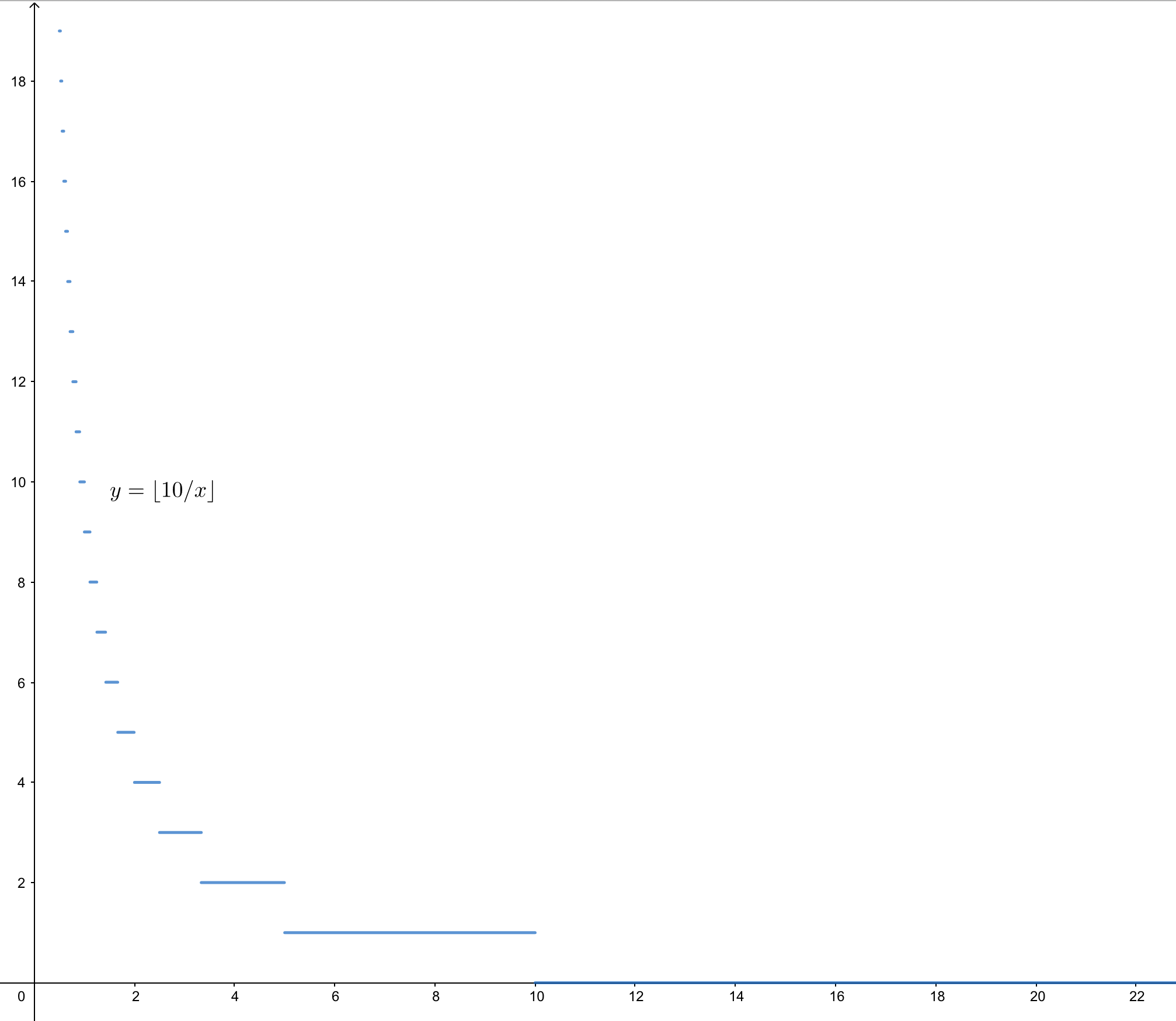
上图是一条 \(f(x) = \lfloor 10 / x \rfloor\) 的图像。

证明该式子最多只有 \(2\sqrt{k}\) 个取值

分段讨论：

• 当 \(i <= \sqrt{k}\) 时，因为 \(i\) 是 \(1\) 到 \(\sqrt{k}\) 的整数，所以最多只有 \(\sqrt{k}\) 个不同的 \(\lfloor k / i \rfloor\) 值。
• 当 \(i > \sqrt{k}\) 时，\(\lfloor k / i \rfloor <= \sqrt{k}\)，又因为式子取整了，所以式子只能取\(1\) 到 \(\sqrt{k}\) 的整数，故最多也只有 \(\sqrt{k}\) 个不同的 \(\lfloor k / i \rfloor\) 值。

综上所述，\(\lfloor k / i \rfloor\) 最多只有 \(2\sqrt{k}\) 个取值

---

有关 当 \(i > \sqrt{k}\) 时，\(\lfloor k / i \rfloor <= \sqrt{k}\) 的证明：

由于下取整，所以 \(\lfloor k / i \rfloor * i <= k\) ①

假设 $\lfloor k / i \rfloor > \sqrt{k} $，有 \(\lfloor k / i \rfloor * i > \lfloor k / i \rfloor * \sqrt{k} > \sqrt{k} ^ 2 = k\)。②

① 与 ② 矛盾

---

通过以上步骤，我们可以知道这个答案由连续 \(2\sqrt{k}\) 段不同的取值组成，那么我们只需要确定每种取值是下界 \(l\) 和 上界 \(r\)。通过 \(\sum_{i = l}^{r} \lfloor k / i \rfloor * i = \sum_{i = l}^{r} \lfloor k / l \rfloor * i = \lfloor k / l \rfloor * (\sum_{i = l}^{r}i)\) 即可求得每一段对答案的贡献。\((\sum_{i = l}^{r}i)\) 可以用等差数列求和公式计算。

已知下界求上界

假设我们知道一段相同取值的下界是 \(x\)，若能求出上界，我们问题便解决了。

猜想若下界是 \(x\)，上界是 \(r = \lfloor k / \lfloor k / x \rfloor \rfloor\)

第一步、求证 \(\lfloor k / x \rfloor = \lfloor k / r \rfloor\)

• 由定义式可知 \(r * \lfloor k / x \rfloor + q = k\) ③，其中 \(0 <= q < \lfloor k / x \rfloor\)，所以 \(\lfloor k / r \rfloor = \lfloor\frac{r * \lfloor k / x \rfloor + q}{r}\rfloor = \lfloor k / x \rfloor + \lfloor \frac{q}{r} \rfloor >= \lfloor k / x \rfloor\)

• \(r >= \lfloor k / (k / x ) \rfloor = x\)，所以 \(\lfloor k / x \rfloor >= \lfloor k / r \rfloor\)

综上 \(\lfloor k / x \rfloor = \lfloor k / r \rfloor\)。

---

第二步、求证 \(\lfloor k / (r + 1) \rfloor \not = \lfloor k / x \rfloor\)

假设 \(\lfloor k / (r + 1) \rfloor = \lfloor k / x \rfloor\)

那么有 \((r + 1) * \lfloor k / x \rfloor + q' = k\)，其中 \(0 <= q < r + 1\)

把式子变化一下：

$r * \lfloor k / x \rfloor + \lfloor k / x \rfloor + q' = k $ ④

③④ 联立，有：

\(\lfloor k / x \rfloor + q' < \lfloor k / x \rfloor\)

因为 \(q' >= 0\)，所以该式子矛盾，故假设不成立。

---

通过这两步及之前的单调性，我们知道 \(\lfloor k / \lfloor k / x \rfloor \rfloor\) 一定是上界

算法

所以算法就很好设计了：

• 设 \(l = 1\)，算出上界 \(r\)。计算这段的贡献
• 使 \(l = r + 1\)，即跳到下一段计算贡献。
• 重复知道算完 \([1, n]\) 里所有段。

\(Tips:\)

1. 当 \(\lfloor k / l \rfloor = 0\) 的时候，显然这段以及后面（有单调性）已经没有贡献了，可以 \(break\)。（或者直接设右端点为 \(n\)）
2. 注意右端点和 \(n\) 取个 \(min\)，因为 $ > n$ 没有贡献了。

#include <cstdio>
#include <iostream>
using namespace std;
typedef long long LL;
int n, k, l, r;
LL ans;
int main() {
	scanf("%d%d", &n, &k);
	ans = (LL)n * k;
	for (l = 1; l <= n; l = r + 1) {
	    if(k / l == 0) break;
		r = min(k / (k / l), n);
		ans -= (LL)(k / l) * (l + r) * (r - l + 1) / 2;
	}
	printf("%lld\n", ans);
	return 0;
}