求lca（模板）

洛谷——P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入输出格式

输入格式：

第一行包含三个正整数N、M、S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来N-1行每行包含两个正整数x、y，表示x结点和y结点之间有一条直接连接的边（数据保证可以构成树）。

接下来M行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。

输出格式：

输出包含M行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入样例#1：

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5

输出样例#1：

4
4
1
4
4

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

该树结构如下：

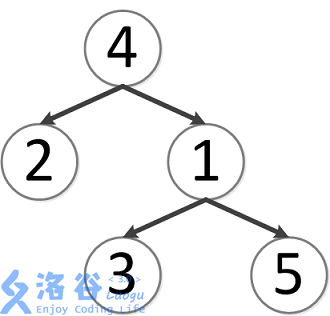
第一次询问：2、4的最近公共祖先，故为4。

第二次询问：3、2的最近公共祖先，故为4。

第三次询问：3、5的最近公共祖先，故为1。

第四次询问：1、2的最近公共祖先，故为4。

第五次询问：4、5的最近公共祖先，故为4。

故输出依次为4、4、1、4、4。

我的这几种做法都是70分，tle，这个题卡vec,把它改掉就好了，由于本人太懒，就暂且不改了

1.用倍增法。

代码：

#include<vector>
#include<stdio.h>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 500001
#define maxn 123456
using namespace std;
vector<int>vec[N];
int n,x,y,fa[N][20],deep[N],m,root;
void dfs(int x)
{
    deep[x]=deep[fa[x][]]+;
    ;fa[x][i];i++)
      fa[x][i+]=fa[fa[x][i]][i];
    ;i<vec[x].size();i++)
    {
        if(!deep[vec[x][i]])
        {
            fa[vec[x][i]][]=x;
            dfs(vec[x][i]);
         }
    }
}
int lca(int x,int y)
{
    if(deep[x]>deep[y])
      swap(x,y);//省下后面进行分类讨论，比较方便
    ;i--)
    {
        if(deep[fa[y][i]]>=deep[x])
          y=fa[y][i];//让一个点进行倍增，直到这两个点的深度相同
    }
    if(x==y) return x;//判断两个点在一条链上的情况
    ;i--)
    {
        if(fa[x][i]!=fa[y][i])
        {
            y=fa[y][i];
            x=fa[x][i];
          }
    }
    ];//这样两点的父亲就是他们的最近公共祖先
}
int main()
{
    scanf("%d%d%d",&n,&m,&root);
    ;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        vec[x].push_back(y);
        vec[y].push_back(x);
    }
    deep[root]=;
    dfs(root);
    ;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));
    }
    ;
}

2.树剖法

#include<vector>
#include<stdio.h>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 500001
#define maxn 123456
using namespace std;
vector<int>vec[N];
int n,m,root,x,y,fa[N],deep[N],size[N],top[N];
int lca(int x,int y)
{
    for( ;top[x]!=top[y];)
    {
        if(deep[top[x]]<deep[top[y]])
         swap(x,y);
        x=fa[x];
    }
    if(deep[x]>deep[y])
     swap(x,y);
    return x;
 }
void dfs(int x)
{
    size[x]=;
    deep[x]=deep[fa[x]]+;
    ;i<vec[x].size();i++)
    {
        if(fa[x]!=vec[x][i])
        {
            fa[vec[x][i]]=x;
            dfs(vec[x][i]);
            size[x]+=size[vec[x][i]];
        }
    }
}
void dfs1(int x)
{
    ;
    if(!top[x])  top[x]=x;
    ;i<vec[x].size();i++)
      if(vec[x][i]!=fa[x]&&size[vec[x][i]]>size[t])
         t=vec[x][i];
    if(t)
    {
        top[t]=top[x];
        dfs1(t);
    }
    ;i<vec[x].size();i++)
     if(vec[x][i]!=fa[x]&&vec[x][i]!=t)
      dfs1(vec[x][i]);
}
int main()
{    scanf("%d%d%d",&n,&m,&root);
    ;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        vec[x].push_back(y);
        vec[y].push_back(x);
    }
    dfs(root);
    dfs1(root);
    ;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));
    }
    ;
}

3.tarjian法

#include<vector>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define N 500001
using namespace std;
vector<int>vec[N],que[N];
int n,m,qx[N],qy[N],x,y,root,fa[N],dad[N],ans[N];
int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}
void dfs(int x)
{
    fa[x]=x;
    ;i<vec[x].size();i++)
     if(vec[x][i]!=dad[x])
      dad[vec[x][i]]=x,dfs(vec[x][i]);
    ;i<que[x].size();i++)
      if(dad[y=qx[que[x][i]]^qy[que[x][i]]^x])
       ans[que[x][i]]=find(y);
    fa[x]=dad[x];
}
int main()
{
    scanf("%d%d%d",&n,&m,&root);
    ;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        vec[x].push_back(y);
        vec[y].push_back(x);
    }
    ;i<=m;i++)
    {
        scanf("%d%d",&qx[i],&qy[i]);
        que[qx[i]].push_back(i);
        que[qy[i]].push_back(i);
    }
    dfs(root);
    ;i<=m;i++)
     printf("%d\n",ans[i]);
    ;
 }